
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Числовые последовательности
|
|
Федеральное агентство по образованию
Воронежский государственный университет
Математический анализ
Числовые последовательности.
Предел числовой последовательности
Учебно-методическое пособие
по специальности 071900 «Информационные системы и технологии»
Для студентов 1 курса очной формы обучения
(издание второе переработанное и дополненное)
Воронеж - 2008
Аннотация издания
Пособие является переработанным и дополненным изданием выпущенного в 2006 году одноименного учебно-методического пособия, созданного на основе опыта преподавания курса математического анализа на факультете компьютерных наук ВГУ. В него включен материал, относящийся к темам «Числовые последовательности» и «Предел числовой последовательности». Каждый параграф содержит справочный материал, набор типовых примеров с решениями и задачи для самостоятельной работы. В пособии приведены варианты заданий, предлагавшихся на второй рубежной аттестации аттестации.
Рекомендовано научно-методическим советом математического факультета ВГУ
Авторы: к.ф-м.н, доцент Сергей Анатольевич Скляднев;
ассистент Светлана Вячеславовна Писарева
Научный редактор: д.ф-м.н, профессор Владимир Алексеевич Костин
Рецензент: д.ф-м.н, профессор Александр Васильевич Лобода
Редактор: О.А. Тихомирова
Ó С.А. Скляднев, С.В. Писарева
Ó Воронежский государственный университет
Числовые последовательности
СПРАВОЧНЫЕ СВЕДЕНИЯ
1.1 Определение числовой последовательности
Если каждому числу n из натурального ряда чисел 1, 2, 3,..., 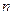 ,... поставлено в соответствие вещественное число
,... поставлено в соответствие вещественное число 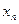 , то множество вещественных чисел
, то множество вещественных чисел  называется числовой последовательностью или просто последовательностью.
называется числовой последовательностью или просто последовательностью.
Числа  называются элементами (членами) последовательности, символ
называются элементами (членами) последовательности, символ 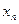 — общим элементом (членом) последовательности, а
— общим элементом (членом) последовательности, а 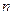 — номером элемента. Последовательность, как правило, обозначают символом
— номером элемента. Последовательность, как правило, обозначают символом 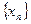 .
.
Последовательности 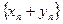 ,
, 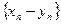 ,
,  ,
, 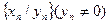 называются соответственно суммой, разностью, произведением и частным двух последовательностей:
называются соответственно суммой, разностью, произведением и частным двух последовательностей: 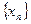 и
и  .
.
Множество значений последовательности может быть как конечным, так и бесконечным, например, множество значений последовательности 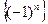 состоит из двух чисел, 1 и -1, множество значений последовательности
состоит из двух чисел, 1 и -1, множество значений последовательности 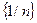 бесконечно. Последовательность, множество значений которой состоит из одного числа, называют стационарной.
бесконечно. Последовательность, множество значений которой состоит из одного числа, называют стационарной.
Последовательность может быть задана с помощью формулы вида
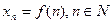 .
.
Формулу, выражающую 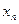 через номер
через номер 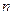 , например,
, например,
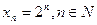 ;
; 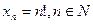 ;
;
называют формулой общего члена последовательности.
Для задания последовательности используют и рекуррентные формулы, т.е. формулы, выражающие 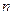 -й член последовательности через члены с меньшими номерами (предшествующие члены). Так определяют арифметическую и геометрическую прогрессии. Другими примерами являются последовательности
-й член последовательности через члены с меньшими номерами (предшествующие члены). Так определяют арифметическую и геометрическую прогрессии. Другими примерами являются последовательности
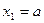 ,
, 
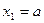 ,
,  ,
, 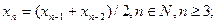
где a, b, c - заданные числа.
Последовательность 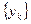 называют подпоследовательностью последовательности
называют подпоследовательностью последовательности  , если есть такая строго возрастающая последовательность номеров
, если есть такая строго возрастающая последовательность номеров 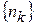 , что для любого
, что для любого 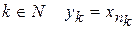 .
.
1.2 Ограниченные последовательности
Последовательность  ограничена снизу, если существует число
ограничена снизу, если существует число  такое, что для всех
такое, что для всех 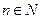 верно неравенство
верно неравенство
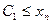 .
.
Число  называют нижней гранью последовательности.
называют нижней гранью последовательности.
Последовательность  ограничена сверху, если существует число
ограничена сверху, если существует число 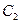 такое, что для всех
такое, что для всех 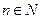 верно неравенство
верно неравенство
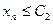 .
.
Число 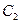 называют верхней гранью последовательности.
называют верхней гранью последовательности.
Последовательность  ограничена, если существуют числа
ограничена, если существуют числа  и
и 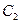 такие, что для всех
такие, что для всех 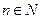 верны неравенства
верны неравенства
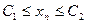 .
.
Это определение равносильно следующему: последовательность  ограничена, если существует число
ограничена, если существует число 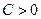 такое, что для всех
такое, что для всех 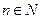 верно неравенство
верно неравенство 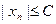 , или
, или
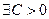
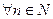 :
: 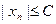 .
.
Следовательно, последовательность ограничена тогда и только тогда, когда ограничено множество ее значений.
Последовательность  не ограничена, если для любого
не ограничена, если для любого 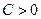 найдется
найдется 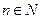 такое, что верно неравенство
такое, что верно неравенство 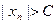 ; или
; или
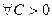
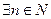 :
: 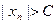 .
.
Аналогично формулируется определение неограниченной сверху (снизу) последовательности.
1.3 Точные грани последовательностей
Число m называют точной нижней гранью (или инфимумом) множества членов последовательности  (записывают
(записывают 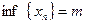 ), если:
), если:
1). 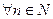
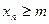 ;
;
2). 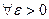
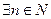 :
:  .
.
Число M называют точной верхней гранью (или супремумом) множества членов последовательности  (записывают
(записывают 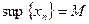 ), если:
), если:
1) 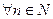
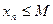 ;
;
2) 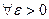
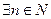 :
: 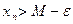 .
.
Член 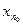 последовательности
последовательности  называют наибольшим (соответственно наименьшим), если
называют наибольшим (соответственно наименьшим), если 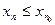 (соответственно
(соответственно  ) для любого
) для любого 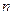 , и обозначают его
, и обозначают его 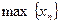 (соответственно
(соответственно 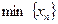 ).
).
Наибольший (соответственно наименьший) член последовательности называют также максимальным (соответственно минимальным).
Если существует 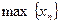 (соответственно
(соответственно 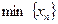 ), то
), то  =
= 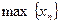 (соответственно
(соответственно 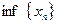 =
= 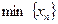 ).
).
Из существования  (соответственно
(соответственно 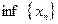 ) не следует существования
) не следует существования 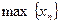 (соответственно
(соответственно 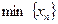 ).
).
1.4 Монотонные последовательности
Последовательность  называют возрастающей (неубывающей), начиная с номера
называют возрастающей (неубывающей), начиная с номера 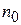 , если для любого
, если для любого 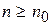 ,
, 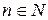 , верно неравенство
, верно неравенство 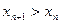
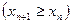 .
.
Последовательность  называют убывающей (невозрастающей), начиная с номера
называют убывающей (невозрастающей), начиная с номера 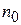 , если для любого
, если для любого 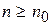 ,
, 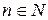 , верно неравенство
, верно неравенство 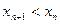
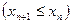 .
.
Невозрастающую или неубывающую, начиная с номера 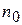 , последовательность называют монотонной, начиная с номера
, последовательность называют монотонной, начиная с номера 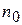 (возрастающую или убывающую — строго монотонной).
(возрастающую или убывающую — строго монотонной).
Последовательность, возрастающую с номера 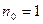 , называют возрастающей (аналогично, убывающей и т. д.).
, называют возрастающей (аналогично, убывающей и т. д.).
ПРИМЕРЫ С РЕШЕНИЯМИ
Пример 1. Дана формула общего члена последовательности  :
: 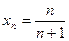 .
.
Написать пять первых членов этой последовательности.
Решение. Подставляя последовательно значения 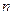 =1, 2, 3, 4, 5 в данную формулу общего члена последовательности, получаем:
=1, 2, 3, 4, 5 в данную формулу общего члена последовательности, получаем:
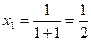 ;
; 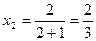 ;
; 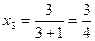 ;
; 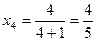 ;
; 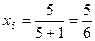 .
.
Пример 2. Доказать, что ограничены последовательности:
1) 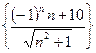 ; 2)
; 2)  .
.
Решение. 1) Поскольку
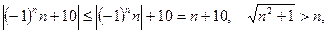 то
то
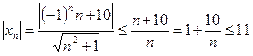 ,
,
что и означает ограниченность  .
.
2) Очевидно, для всех 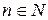 имеем
имеем
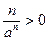 .
.
Так как 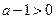 , то, применив неравенство Бернулли, получим, что для всех
, то, применив неравенство Бернулли, получим, что для всех 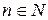
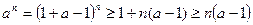 ,
,
откуда
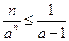 .
.
Таким образом, для всех 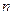 верны неравенства
верны неравенства
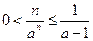 ,
,
т. е. последовательность ограничена.
Пример 3. Доказать, что не ограничены последовательности:
1) 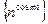 ; 2)
; 2)  .
.
Решение. 1) Если  , то
, то  и
и 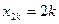 . Пусть
. Пусть 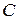 - произвольное положительное число. Возьмем четное число
- произвольное положительное число. Возьмем четное число 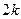 , большее
, большее 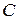 (например,
(например, 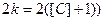 ; тогда
; тогда 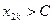 , т. е. данная последовательность не ограничена.
, т. е. данная последовательность не ограничена.
2) Из формулы общего члена последовательности имеем:
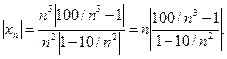
И, если 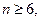 то
то

Но так как 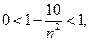 то
то
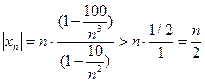 .
.
Для произвольного положительного числа  возьмем
возьмем 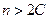 (например,
(например, 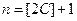 ); тогда
); тогда  , и, значит, данная последовательность не ограничена.
, и, значит, данная последовательность не ограничена.
Пример 4. Доказать, что последовательность 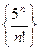 , строго убывает, начиная с некоторого номера.
, строго убывает, начиная с некоторого номера.
Решение. Рассмотрим отношение
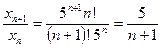 .
.
Видно, что при 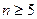
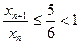 ,
,
и, значит,  (так как
(так как 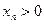 ). Итак, данная последовательность строго убывает, начиная с номера
). Итак, данная последовательность строго убывает, начиная с номера 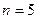 .
.
Пример 5. Доказать, что последовательность  строго возрастает.
строго возрастает.
Решение. Рассмотрим отношение
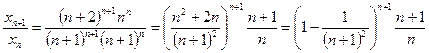 .
.
Для любого 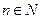 из неравенства Бернулли получаем:
из неравенства Бернулли получаем:
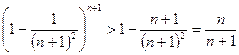 .
.
Откуда следует, что для любого 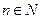
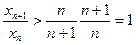 ,
,
т.е. 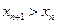 , что и доказывает наше утверждение.
, что и доказывает наше утверждение.
ЗАДАЧИ
Задача 1. Написать пять первых членов каждой из последовательностей:
1) 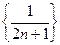 ; 2)
; 2) 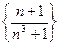 ; 3)
; 3) 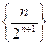 ; 4)
; 4) 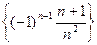 ; 5)
; 5) 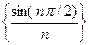 .
.
Задача 2. Зная несколько первых членов последовательности, написать формулу общего члена последовательностей (выдвинуть какую-либо гипотезу)
1) 1; 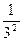 ;
;  ;
; 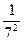 ; 2) 1;
; 2) 1; 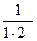 ;
; 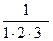 ;
; 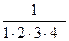 …;
…;
3) 1; 2 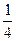 ; 2
; 2 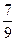 ; 3
; 3  ; 3
; 3  ;...; 4) 2; 10; 26; 82; 242; 730;...; 5) -1; 1; -1; 1; -1;....
;...; 4) 2; 10; 26; 82; 242; 730;...; 5) -1; 1; -1; 1; -1;....
Задача 3. Написать пять первых членов и формулу общего члена каждой из последовательностей, заданных рекуррентными соотношениями:
1) x1 = 1, xn+1 = xn!; 2) x1 = 1, xn+1 = xn+3; 3) x1 = 1, xn+1 = (n+1) xn;
4) x1 =2, xn+1 =3xn; 5). x1 = 1, xn+1 = x1 + x2 +…+ xn
Задача 4. Выяснить, какие из чисел 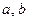 являются членами последовательности
являются членами последовательности  , если:
, если:
1)  ;
;
2) 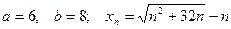 ;
;
3) 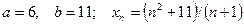 ;
;
4) 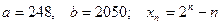 .
.
Задача 5. Является ли последовательность 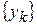 подпоследовательностью последовательности
подпоследовательностью последовательности  , если
, если
1) 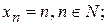
а)  б)
б) 
2) 
а) 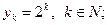 б)
б) 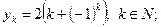
3) 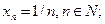
а) 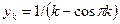 ,
, 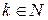 ; б)
; б) 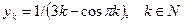 .
.
Задача 6. Какие из последовательностей являются ограниченными:
1) 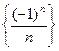 ; 2)
; 2) 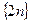 ; 3)
; 3) 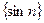 ; 4)
; 4) 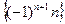 ; 5)
; 5) 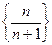 ; 6)
; 6) 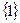 ; 7)
; 7) 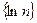 .
.
Задача 7. Доказать ограниченность последовательностей:
1) 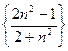 ; 2)
; 2) 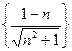 ; 3)
; 3)  ; 4)
; 4) 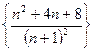 ; 5)
; 5)  .
.
Задача 8. Доказать неограниченность последовательностей:
1) 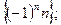 2)
2) 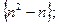 3)
3) 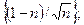 4)
4) 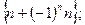
5) 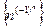 ; 6)
; 6) 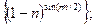 7)
7) 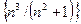 ; 8)
; 8)  .
.
Задача 9. Доказать, что данные последовательности монотонны, начиная с некоторого номера (своего для каждой последовательности):
1) 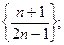 2)
2) 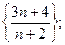 3)
3) 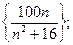 4)
4) 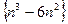 ; 5)
; 5) 
6) 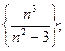 7)
7) 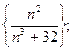 8)
8) 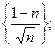 9)
9) 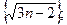 10)
10) 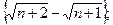
11) 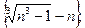 12)
12) 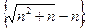 13)
13)  14)
14) 
Задача 10. Доказать, что данные последовательности убывают, начиная с некоторого номера (своего для каждой последовательности):
1) 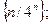 2)
2)  3)
3) 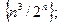 4)
4) 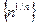 .
.
|
|