Теорема 3.5.

Планы соответственно прямой и двойственной ЗЛП являются оптимальными тогда и только тогда, когда

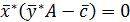(3.28)

Условия (3.28) называются условиями дополнительной нежесткости.

Необходимость.

Пусть и являются соответственно решениями ИЗ и ДЗ, тогда (1)

(2)

(3)

(теорема 3.4) (4)

Умножая равенство (1) слева на и учитывая (4), получим:

,

откуда или .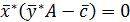

Достаточность.

Пусть и являются соответственно планами ИЗ и ДЗ, для которых выполняется условие (3.28).

Для того чтобы доказать оптимальность этих планов, достаточно доказать равенство целевых функций ИЗ и ДЗ (Теорема 3.4, следствие 3).

Имеем:

(1)

(2)

(3)

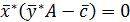(4)

Из (4) следует, что

(5)

Умножая равенство (1) слева на , получим:

, (6)

т.к. , то с учетом (5) и (6) имеем:

.

Примечание 1. Для основной ЗЛП и двойственной к ней ЗЛП условия нежесткости имеют вид:

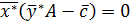. (3.29)

Примечание 2. Если прямая ЗЛП записана не в канонической форме, то условия дополнительной нежесткости для этой ЗЛП и двойственной к ней ЗЛП могут быть записаны в следующем виде:

если х_j^* > 0, то ,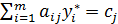

если то y_i^* = 0, (3.30)

если y_i^* > 0, то

если , то х_j^* = 0.

Теоремы 3.2-3.5 называются основными теоремами двойственности.

Кроме этих теорем можно доказать еще четыре теоремы двойственности.