
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теорема 2.24.
|
|
Если  то вектор
то вектор  является опорным планом основной задачи линейного программирования. Если
является опорным планом основной задачи линейного программирования. Если  < 0, то множество планов P основной задачи линейного программирования пусто.
< 0, то множество планов P основной задачи линейного программирования пусто.
Доказательство.
Пусть 
Это означает, что все искусственные компоненты оптимального опорного
плана  вспомогательной задачи линейного программирования равны нулю,
вспомогательной задачи линейного программирования равны нулю,
т.е.  (2.90)
(2.90)
и вектор  принадлежит множеству P´ M.
принадлежит множеству P´ M.
Но тогда вектор  является планом основной задачи линейного программирования, множество P´ не пусто и, следовательно, основная задача имеет хотя бы один опорный план.
является планом основной задачи линейного программирования, множество P´ не пусто и, следовательно, основная задача имеет хотя бы один опорный план.
При этом в процессе решения вспомогательной задачи симплексным методом могут представиться следующие два случая:
1. На S – й итерации симплексного метода ни одна из искусственных переменных не является базисной, т.е.  Тогда матрица (2.89) является K – матрицей основной задачи линейного программирования, а план
Тогда матрица (2.89) является K – матрицей основной задачи линейного программирования, а план  - опорным планом основной задачи, определяемым этой K -матрицей.
- опорным планом основной задачи, определяемым этой K -матрицей.
2. На S – й итерации симплексного метода в числе базисных оказались искусственные переменные, например, 

т.е.

Тогда в силу равенства (2.90) p базисных компонент вектора  равны нулю:
равны нулю:

и, следовательно, он является вырожденным оптимальным опорным планом вспомогательной задачи линейного программирования, а матрица  содержит p< m единичных столбцов и не является K – матрицей основной задачи.
содержит p< m единичных столбцов и не является K – матрицей основной задачи.
Однако в этом случае матрицу  можно преобразовать в K – матрицу основной задачи линейного программирования, определяющую ее исходный опорный план
можно преобразовать в K – матрицу основной задачи линейного программирования, определяющую ее исходный опорный план  .
.
Для этой цели рассмотрим любую r - ю строку из первых p строк матрицы  (r = 1, 2, …, p).
(r = 1, 2, …, p).
Среди элементов  этой строки есть хотя бы один элемент, отличный от нуля, так как в противном случае ранг матрицы A меньше m.
этой строки есть хотя бы один элемент, отличный от нуля, так как в противном случае ранг матрицы A меньше m.
Выберем этот элемент в качестве направляющего и совершим один шаг метода Жордана – Гаусса преобразования матрицы  с выбранным направляющим элементом. В результате базисная искусственная переменная
с выбранным направляющим элементом. В результате базисная искусственная переменная  будет заменена одной из основных переменных
будет заменена одной из основных переменных  , а элементы (n+1) – го столбца матрицы не изменятся.
, а элементы (n+1) – го столбца матрицы не изменятся.
После p таких шагов метода Жордана – Гаусса матрица  будет преобразована в K - матрицу основной задачи линейного программирования, определяющую ее исходный опорный план
будет преобразована в K - матрицу основной задачи линейного программирования, определяющую ее исходный опорный план  .
.
Очевидно, что этот опорный план будет вырожденным.
Пусть теперь  < 0, т.е. при решении вспомогательной задачи линейного программирования на S – й итерации симплексного метода в числе базисных оказались искусственные переменные, причем компоненты опорного плана
< 0, т.е. при решении вспомогательной задачи линейного программирования на S – й итерации симплексного метода в числе базисных оказались искусственные переменные, причем компоненты опорного плана  , являющиеся значениями этих переменных, не равны нулю.
, являющиеся значениями этих переменных, не равны нулю.
Предположим, что в рассматриваемом случае множество планов P´ основной задачи линейного программирования не пусто и существует вектор  который
который
удовлетворяет ограничениям (2.86)-(2.88).
Но тогда вектор  - план вспомогательной задачи линейного программирования и такой, что
- план вспомогательной задачи линейного программирования и такой, что 
Следовательно,  <
<  , а это противоречит предложению об оптимальности вектора
, а это противоречит предложению об оптимальности вектора  .
.
Таким образом, решая вспомогательную задачу линейного программирования симплекс-методом, мы либо находим исходный опорный план основной задачи, либо убеждаемся, что множество планов P´ основной задачи линейного программирования пусто. После того, как найден исходный опорный план задачи линейного программирования, ее можно в принципе решать симплексным методом, т.е. практически решение основной задачи осуществляется в два этапа.
Пример 2.13. Рассмотрим задачу
 =0.4X1+0.3X2+0.1X3+0.1X5+0.2X6 (1)
=0.4X1+0.3X2+0.1X3+0.1X5+0.2X6 (1)
2X2+2X3+4X4+X5=150
X1+X2+2X5=200 (2)
X1+X3+2X6=300
 ; j=1,..., 6 (3)
; j=1,..., 6 (3)
Так как ограничения (2) рассматриваемой ЗЛП уже имеют вид строгих равенств, то для приведения ее к каноническому виду достаточно только изменить знак функции  на противоположный и рассмотреть задачу нахождения
на противоположный и рассмотреть задачу нахождения  -0.4X1-0.3X2-0.1X3-0.1X5-0.2X6 (4) при тех же ограничениях (3.2)-(3).
-0.4X1-0.3X2-0.1X3-0.1X5-0.2X6 (4) при тех же ограничениях (3.2)-(3).
Рассмотрим расширенную матрицу системы уравнений (2)

Так как расширенная матрица не содержит единичной подматрицы порядка 3, то она не является К -матрицей ЗЛП и, следовательно, к задаче (2)-(4) не может быть применен симплекс-метод.
Рассмотрим метод отыскания исходного опорного плана (К -матрицы)- метод искусcтвенного базиса.
Для задачи (2)-(4) запишем ВЗ:
 -(U1+U2+U3)
-(U1+U2+U3)  max (5)
max (5)
2X1+2X3+4X4+X5+U1=150
X1+X2+2X5+U2=200 (6)
X1+X3+2X6+U3=300
 (7)
(7)
Результаты первого этапа представлены в табл. 2.7
Таблица 2.7
| -1 | -1 | -1 | ||||||||||||||
| S | i | 
| 
| 
| 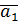
| 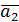
| 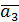
| 
| 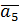
| 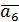
| 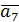
| 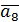
| 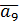
| 
| ||
| -1 | 37.5 | |||||||||||||||
| -1 | - | |||||||||||||||
| -1 | - | |||||||||||||||

| -650 | -2 | -3 | -3 | -4 | -3 | -2 | |||||||||
| 37.5 | 0.5 | 0.5 | 0.25 | 0.25 | - | - | ||||||||||
| -1 | - | |||||||||||||||
| -1 | - | |||||||||||||||

| -500 | -2 | -1 | -1 | -2 | -2 | ||||||||||
| 37.5 | 0.5 | 0.5 | 0.25 | 0.25 | - | |||||||||||
| - | ||||||||||||||||
| -1 | -1 | -2 | -1 | |||||||||||||

| -100 | -1 | -2 | |||||||||||||
| 37.5 | 0.5 | 0.5 | 0.25 | 0.25 | ||||||||||||
| -0.5 | 0.5 | -1 | -0.5 | 0.5 | ||||||||||||

|
На третьей итерации симплексного метода получен оптимальный план вспомогательной задачи:  =(200; 0; 0; 37.5; 0; 50; 0; 0; 0),
=(200; 0; 0; 37.5; 0; 50; 0; 0; 0),
в котором ни одна из искусственных переменных не является базисной, следовательно, вектор  =(200; 0; 0; 37.5; 0; 50) является невырожденным опорным планом исходной задачи, определяемым К -матрицей.
=(200; 0; 0; 37.5; 0; 50) является невырожденным опорным планом исходной задачи, определяемым К -матрицей.

На втором этапе решаем задачу
max(-0.4X1-0.3X2-0.1X3-0.1X5-0.2X6)
 .
.
Решение приведено в табл. 2.8.
Таблица 2.8.
| -0.4 | -0.3 | -0.1 | -0.1 | -0.2 | |||||||
| S | i | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| 37.5 | 0.5 | 0.5 | 0.25 | ||||||||
| -0.4 | |||||||||||
| -0.2 | -0.5 | 0.5 | -1 | - | |||||||

| -90 | -0.5 | |||||||||
| 12.5 | -0.125 | 0.375 | 0.5 | ||||||||
| -0.1 | 0.5 | 0.5 | - | ||||||||
| -0.2 | |||||||||||

| -40 | 0.25 | 0.25 | ||||||||
| -0.1 | -0.25 | 0.75 | |||||||||
| -0.1 | 0.5 | ||||||||||
| -0.2 | 137.5 | 0.625 | -0.375 | -1 | |||||||

| 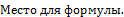 -40 -40
| 0.25 | 0.25 |
На первой итерации (табл. 2.8.) второго этапа получен оптимальный план исходной задачи  1=(0; 0; 12.5; 100; 150) и
1=(0; 0; 12.5; 100; 150) и  =40.
=40.
Так как  =0, а вектор
=0, а вектор  не является базисным, то его можно ввести в базис, и при этом в соответствии с формулой (3.28) значение целевой функции не изменится, т.е. на второй итерации можно получить еще один оптимальный план исходной задачи
не является базисным, то его можно ввести в базис, и при этом в соответствии с формулой (3.28) значение целевой функции не изменится, т.е. на второй итерации можно получить еще один оптимальный план исходной задачи
 2=(0; 0.25; 0; 100; 137.5) и
2=(0; 0.25; 0; 100; 137.5) и  =40.
=40.
Исходная задача имеет бесчисленное множество решений, задаваемое формулой  (8)
(8)
Пример 2.14. Решить ЗЛП:
max(2X1-X2-X4)
X1-2X2+X3=10
-2X1-X2-2X4  18 (9)
18 (9)
3X1+2X2+X4  36
36

Приведем ЗЛП (9) к каноническому виду
max(2X1-X2-X4)
X1-2X2+X3=10
-2X1-X2-2X4- S1 =18 (10)
3X1+2X2+X4-S2 =36

Расширенная матрица системы линейных уравнений (10)
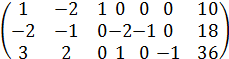
не является К -матрицей ЗЛП (10), т.к. не содержит единичной подматрицы.
Запишем вспомогательную задачу для ЗЛП (10). Т.к. матрица  содержит один единичный вектор
содержит один единичный вектор 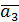 =(1; 0; 0), то при формулировке ВЗ достаточно ввести лишь две искусственные переменные U1; U2 во второе и третье уравнения системы (10).
=(1; 0; 0), то при формулировке ВЗ достаточно ввести лишь две искусственные переменные U1; U2 во второе и третье уравнения системы (10).
Итак, ВЗ имеет вид
 -(U1+U2)
-(U1+U2)  max
max
X1-2X2+X3=10
-2X1-X2-2X4-X5+U1=18 (11)
3X1+2X2+X4-X6+U2=36
 ; U1, U2
; U1, U2  0
0
Решение ВЗ приведено в табл 2.9.
Таблица 2.9
| -1 | -1 | ||||||||||||
| S | i | 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
| 
|
| -1 | -2 | - | |||||||||||
| -1 | -2 | -1 | -2 | -1 | - | ||||||||
| -1 | -1 | ||||||||||||

| -54 | -1 | -1 | ||||||||||
| -1 | |||||||||||||
| -1 | -0.5 | -1.5 | -1 | -0.5 | 0.5 | ||||||||
| 1.5 | 0.5 | -0.5 | 0.5 | ||||||||||

| -36 | 0.5 | 1.5 | 0.5 | 0.5 |
На первой итерации получен оптимальный план.
 =(0; 18; 46; 0; 0; 36; 0).
=(0; 18; 46; 0; 0; 36; 0).
Т.к. вектор имеет отличную от нуля искусственную переменную U1=36, то множество планов ЗЛП (9) пусто в силу несовместности системы уравнений (10).
2.8. Модифицированный симплекс-метод
|
|