
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Раздел 1, Строительное материаловедение 4 страница
|
|
R tf.op = у/ ЕЭ /а, (1.28)
где Е - модуль упругости; Э - поверхностная энергия твердого тела на 1 см2, а - межатомное расстояние (в среднем 210 8 см).
Теоретическая прочность материала тем выше, чем больше модуль упругости и поверхностная энергия и чем меньше межатомное расстояние.
Согласно приведенному выражению прочность твердого тела должна находиться между значениями Е/5 и £ /10. Например, теоретическая прочность стали 30000 МПа, в то время как прочность обычной стали около 400 МПа, а специальной проволоки - 3000 МПа. Теоретическая прочность стекла при комнатной температуре - 14000 МПа, прочность на растяжение тонких стеклянных волокон (толщиной 3-5 мкм) - 3500-5000 МПа, а обыкновенного стекла - только 70-150 МПа. Используется сравнительно небольшая доля потенциальной прочности материала; прочность понижается благодаря наличию пор, трещин и дефектов структуры материала.
Влияние строения на прочность
Прочность материала одного и того же состава зависит от его
пористости. На рис. 1.11 представлен график прочности цементного бетона, показывающий, что увеличение пористости с 12, 4 до 15, 2% снизило прочность при сжатии с 37, 5 до 26 МПа. Подобная зависимость характерна и для других материалов (известняка, керамических материалов и пр.).
Реальные кристаллические материалы имеют большее или меньшее количество точечных дефектов. Одни из них заключаются в том, что некоторые атомы или ионы смещены в другие положения и могут располагаться даже между узлами кристаллической решетки. Их нормальные места остаются свободными и затем замещаются другими ионами. Следовательно, в узлах решетки могут быть свободные места (вакансии). Другого рода дефекты возникают в результате размещения посторонних атомов или ионов примеси в узлах решетки, где они заменяют основное вещество (примеси замещения), или между ними (примеси внедрения).
Свойства кристаллических материалов зависят от дислокаций кристаллов.
Дислокация - это всегда одномерный (линейный) дефект кристаллической решетки, возникающий или в процессе образования кристалла, или в результате последующих механических, тепловых и других воздействий. Дислокации бывают краевые, винтовые и смешанные - криволинейные.
| 3 40 gtS I* 30 г S а |
| 20 т-ч п |
| £ |
| 12 13 14 15 Пористость бетона, % Рис. 1.11. Кривая зависимости прочности цементного бетона от пористости |
| / | ||||||
| / | ||||||
| / | <,, | р—1 | ||||
| -> | X/--/-/- | |||||
| / |
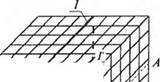
| Рис. 1, 12. Кривая дислокации в кристаллической решетке: / - экстраплоскость |
На рис. 1.12 схематически изображена краевая дислокация. Отклонение от идеального строения кристалла вызвано тем, что один слой атомов (он расположен на
рисунке в экстраплоскости) по каким- то причинам оказался незавершенным. Кромка 1-Г " лишнего" слоя атомов образует линейный дефект, называемый краевой дислокацией (она обозначена на рис. 1.11 знаком X). По обе стороны от кромки экстраплоскости атомы сдвинуты на угол, соответствующий теоретической плоскости кристалла на сдвиг. Стоит приложить внешнее усилие, значительно меньшее теоретической прочности данного кристалла, чтобы осуществить сдвиг на одно межатомное расстояние в плоскости А-А, нормальной к экстраплоскости (рис. 1.13).
Продолжая нагружать кристалл, перемещаем дислокацию из одного ряда атомов в другой, пока не вытолкнем дислокацию на грань кристалла. Механизм скольжения, основанный на движении дислокации, может быть сопоставлен с перемещением по полу ковра с предварительно созданной складкой (рис. 1.14). При таком способе требуется значительно меньшее усилие, чем в случае перемещения ковра как единого целого.
Дислокационная теория рассматри-
вает пластический сдвиг в кристалли- — гтг'^^йВ''-" fr,,.,.; ^-, - —
ческих материалах как скольжение
путем движения дислокации. Под- Рис. 1.14. Складка ковра вижность дислокации зависит от того, в качестве модели скольжения: насколько легко межатомная связь АА'-ВВ'- перемещение ковра может быть разрушена и вновь восстановлена; ведь каждый раз, когда дислокация перемещается на один шаг (межатомное расстояние), должны рваться старые связи и устанавливаться новые. В этом отношении предпочтительнее связи, обеспечивающие одинаковое притяжение во всех направлениях: металлическая и ионная. Дислокации в ковалентных кристаллах при нормальной температуре малоподвижны, так как ковалентная связь является направленной, наиболее прочной и жесткой.
| j | S | ||||
| Л --. | J | ||||
| г | г | S' | If' | ||
| Рис. 1.13. Схема пластического сдвига путем движения дислокации |
Дислокации присутствуют почти во всех кристаллических материалах. Они значительно понижают прочность монокристаллов, но зато придают пластичность поликристаллическим телам с металлической связью, делают металл ковким, затрудняют распространение трещин. Теоретическая прочность железа на сдвиг около 7000 МПа, но практически кристалл очень чистого железа
сдвигается при напряжении, меньшем в 1000 раз, - около 7 МПа; для рядовых сталей прочность на сдвиг 150-250 МПа, для высокопрочных 1500 МПа. Доказательством, подтверждающим объяснение низкой прочности кристаллов движением дислокаций, являются результаты изучения механических свойств " усов". Эти нитевидные кристаллы различных материалов, выращенные без краевых дислокаций, способны претерпевать упругую деформацию до 5-6% без признаков пластического течения. Бездислокационные " усы" способны выдержать напряжения сдвига, достигающие 5% от модуля сдвига; это на несколько порядков больше, чем у обычных кристаллов. В реальности дислокаций убеждают и непосредственные наблюдения. Те места, где дислокации выходят на поверхность, выявляются с помощью химического травления в виде " оспинок" - ямок травления.
Плотность дислокаций (т.е. число дислокаций, пересекающих площадь в 1 см2) может быть весьма велика - 107 - 105 (в отожженных металлах). При механических воздействиях дислокации перемещаются, взаимодействуют между собой и порождают новые дислокации, в особенности в местах концентрации напряжений. В результате этого их плотность возрастает до 1010 - 1013 (в сильно наклепанных металлах). Когда дислокаций много (больше некоторой критической плотности), они переплетаются (словно спутанные нитки), тормозят перемещение друг друга, в результате материал упрочняется. Однако при дальнейшем деформировании материал может сделаться хрупким.
Вакансии в кристаллической решетке, межузловые (внедренные) атомы, дислокации играют важную роль в процессах диффузии, повышают химическую активность, что используется, в частности, в технологии быстротвердеющих цементов. Однако наличие дислокаций и дефектов структуры в готовом материале снижает его стойкость, так как деформированные межатомные связи (как и места концентрации напряжений) более уязвимы для химических и физических воздействий среды. Следовательно, дислокации следует рассматривать как структурный фактор, регулирующий комплекс наиболее важных свойств кристаллических материалов.
Механика разрушения
Различают хрупкое и пластическое разрушение твердых тел. Хрупкое разрушение сопровождается малой предшествующей пластической деформацией, поэтому хрупкость определяют как свойство материала разрушаться " внезапно", не претерпевая су
щественной деформации. Хрупкость присуща не только кристаллическим, но и стеклообразным и даже полимерным материалам.
Разрушению пластичных (вязких) материалов предшествует изменение формы и большая деформация.
Большинство материалов при понижении температуры охрупчи- ваются, у них происходит переход от пластического разрушения к хрупкому. Так ведут себя битумные материалы, некоторые полимеры, металлы и др.
Хрупкое разрушение происходит в результате образования и быстрого роста одной или нескольких трещин при возрастающей нагрузке.
Трещина (как и надрез) вызывает концентрацию напряжений около ее вершины (рис. 1.15). В этом месте напряжение оказывается значительно большим, чем можно ожидать из простого уменьшения площади поперечного сечения.
Напряжение о на конце трещины зависит от номинального напряжения о„, длины (глубины) трещины / и радиуса кривизны в вершине трещины г.
< т, = а(\ + 2уЦ77) (1.29)
Коэффициент концентрации напряжений а А. = cr[\ + 2^l / г J может
быть равен 100 и даже 1000, если радиус вершины трещины соизмерим с радиусом атома, хотя глубина трещины лишь 0, 1 и 10 мкм. Следовательно, местное напряжение может превысить 7000 МПа при номинальном (т.е. среднем по сечению) напряжений 35-100 МПа. Трещина как бы разрезает атомные цепочки, и значительная часть нагрузки, которую несли разрезанные атомные цепочки, приходится теперь на атомную связь у конца трещины. Перегруженная связь лопнет раньше других и положение ухудшится, так как следующее звено будет еще больше перегружено. Таким образом, трещина становится тем инструментом, с помощью которого приложенная извне слабая сила рвет прочные межатомные связи.
| < N + |
| т |
| П ^ f Рис. 1.15. Концентрация напряжений в пластине с трещиной |
При распространении трещины материал вблизи трещины разгружается, и вследствие этого выделяется энергия деформации. Объем, в котором выделяется энергия, изображается на рис. 1.15 как половина объема цилиндра единичной высоты, численно
равного л 1: /2. Выделенная энергия ид зависит от приложенного напряжения а, модуля упругости Е и глубины трещины / (половина длины внутренней трещины);
ид = ~Ть(130)
Образование двух новых поверхностей трещины требует затрат энергии
ип=2Э, 1, (1.31)
где Э, - поверхностная энергия единицы площади поверхности.
Трещина будет самопроизвольно расти, если длина трещины превышает некоторую " критическую длину Гриффитса" ", при которой освобождающаяся энергия упругой деформации больше энергии образующихся новых поверхностей, тогда
я/ < т/Е = 2Э„ (1.32)
откуда
сг= (2Э, E/nl)" 2. (1.33)
Напряжение, необходимое для разрушения растянутой пластины, возрастает у материалов с высоким модулем упругости и большей поверхностной энергией, оно уменьшается при наличии более глубоких поверхностных трещин.
В данном материале для каждого напряжения существует своя критическая длина трещин. Трещины, глубина которых превышает /д-р, способны при данном напряжении а самопроизвольно расти со скоростью, приближающейся к скорости распростране' ния упругой волны (1, 5-2 км/с).
Сжимающие усилия, в отличие от растягивающих могут передаваться через трещины, не вызывая концентрации напряжений. Поэтому хрупкие материалы всегда оказываются значительно прочнее при сжатии, чем при растяжении. Например, у природных каменных материалов (гранит и др.) предел прочности при растяжении составляет всего 1/40-1/60 предела прочности при сжатии. Хрупкие материалы также плохо сопротивляются удару и взрыву.
Торможение трещин при помощи создаваемых в материале внутренних поверхностей раздела используется в современных композиционных материалах.
Механизм торможения трещины основан на том, что при распространении трещины кроме напряжений, перпендикулярных трещине, достигающих максимума в ее вершине, возникает растяжение в направлении, параллельном трещине. Растягивающее напряжение, параллельное трещине, равно нулю в вершине трещины и достигает максимума впереди трещины на расстоянии одного-двух атомных размеров от ее вершины. В растянутом материале отношение максимального напряжения, параллельного трещине, к максимальному напряжению, направленному перпендикулярно ее поверхности, равно приблизительно 1/5. Если прочность сцепления на поверхности раздела больше 1/5 прочности материала, то поверхность не разрушится, трещина ее только пересечет и поведение материала не изменится, т.е. он останется хрупким. Если же прочность сцепления меньше 1/5 прочности на растяжение самого материала, то прежде чем трещина достигнет поверхности раздела, последняя будет разрушена на небольшом участке и образуется ловушка, способная остановить трещину (рис. 1.16).
| Рис. 1.16.Схема торможения трещин |
Кончик трещины, который был очень малым, при встрече с поверхностью раздела становится очень большим, устраняется концентрация напряжений в вершине трещины и тенденция к ее распространению (рис. 1.17).
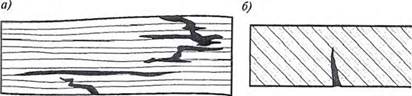 Рис. 1.17. Влияние внутренних поверхностей на торможение трещин: а) волокнистый материал, содержащий внутренние поверхности; б) однородный материал
Рис. 1.17. Влияние внутренних поверхностей на торможение трещин: а) волокнистый материал, содержащий внутренние поверхности; б) однородный материал
|
Модели механических свойств
Механические свойства материалов моделируют, используя реологические факторы: упругость, пластичность и вязкость.
Реология - наука о деформациях и текучести вещества, исследующая различные деформации материалов в зависимости от напряжений.
Вязкость - способность материала поглощать механическую энергию при деформации образца.
Для моделирования поведения упругого материала используют пружину. Упругая деформация идеального тела возникает тотчас после приложения силы и не зависит от времени, как это показано на рис. 1.18. После снятия нагрузки деформация становится равной нулю, следовательно, деформация упругого твердого тела постоянна и обратима.
| (1.34) |
Идеальная (ньютоновская) жидкость подчиняется уравнению вязкого течения
£ ВЯЗК = Tt/rj,
где г- напряжение сдвига (Па); l - время (с); т] - вязкость (Па с).
| О) |
| б) |
| -о! |
| Время |
| Рис. 1.18. Модель идеального (подчиняющегося закону Гука) твердого тела: а) график упругой деформации; б) модель-пружина |
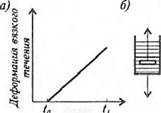
Деформация вязкого течения при постоянном напряжении сдвига возрастает пропорционально времени (рис. 1.19, а). Поведение жидкости моделируют демпфером (рис. 1.19, б), в котором поршень перемещается под действием приложенных сил, при этом жидкость протекает через кольцевой зазор между стенками цилиндра и поршнем.
Поведение материалов, сочетающих упругие и вязкие свойства, можно описать с помощью модели Максвелла[3], состоящей из пружины и демпфера, соединенных последовательно (рис. 1.20, а) при постоянном напряжении. В первый момент времени t„ сопротивление создается упругим элементом и возникает упругая деформация £ УПр, сохраняющаяся неизменной при постоянном напряжении. В период времени от 1„ до t, деформация возрастает вследствие вязкого течения (оно моделируется демпфером, при-
" Д.Максвелл (1831-1879), английский физик, создатель классической электродинамики.
соединенным к пружине). В момент времени t, при снятии нагрузки упругая составляющая деформации равна нулю, но вязкое смещение евязк сохраняется, так как оно необратимо. Следовательно, общая деформация s асфальтобетона, пластика и т.п. содержит упругую и вязкую составляющую:
 Время
Рис. 1.19. Модель идеальной (ньютоновской) жидкости: а) график деформации вязкого течения; б) модель-демпфер
Время
Рис. 1.19. Модель идеальной (ньютоновской) жидкости: а) график деформации вязкого течения; б) модель-демпфер
|
| б) |
| Г, |
а)
-V
х s
§.ч>
•V
ВЯЗК-
В соответствии с законом Гука и приведенной выше формулой для £ вязк получаем следующее уравнение упруго-вязкой деформации:
с =а/Е + а t/rj,
в — с? (1/Е + I/tj). (1.36)
Соответствующий график приведен на рис. 1.20, б. Примером вязкого течения является след шин, вдавившихся в асфальтовое покрытие дороги. Он напоминает о повышенной склонности к вязкому течению материала покрытия в жаркую погоду. При высокой температуре вязкое течение проявляется у стекла, металла и других твердых материалов.
Релаксация напряжений
Релаксация - свойство материала самопроизвольно снижать напряжения при условии, что начальная величина деформации остается неизменной.
| (1.35) |
Модели деформации твердых тел дают возможность получить количественную характеристику скорости релаксационных явлений, протекающих в полимерных и других строительных мате
риалах. Если быстро деформировать тело (например, полимер), сохраняя деформацию постоянной, то напряжение постепенно уменьшается. Деформация вызывает перестройку внутренней структуры тела, и требуется некоторый промежуток времени, пока все частицы тела придут в равновесие в соответствии с новыми условиями.
Элементарная модель релаксации напряжений при постоянной деформации представляет собой последовательное соединение пружины и демпфера (модель Максвелла). Для этой модели общая деформация е равна сумме упругой и вязкой составляющих (рис. 1.20)
е = еУПР + евязк = const. (1.37)
Следовательно,
deyn/dt = -eB„3l/dt. (1.38)
Поскольку £ уш> = ст/Е, а £ вязк = -crt/tj, получим
(do/dt)- (1/Е) ~-< у/г\, ' (1.39)
откуда
^ = (1.40)
о" 7
Введем постоянную времени релаксации Л = tj/E, тогда
(1.41)
где о - напряжение по прошествии времени /; а,, - первоначальное напряжение. Из формулы видно, что релаксация напряжения следует экспоненциальному закону (рис. Время > 1.21). Скорость релаксации Рис. 1.21. Релаксация напряжений напряжения характеризуется по постоянной деформации временем релаксации - промежутком времени, в течение которого напряжение уменьшается в е раз по сравнению с первоначальным (где е - основание натуральных логарифмов).

Дсформативные свойства материалов зависят от температуры. При нагревании они размягчаются и переходят в пиропластиче- ское (глина, стекло и др.) или каучукоподобное (линейные полимеры) состояние, затем плавятся и становятся жидкотекучими. Следовательно, в зависимости от температуры материал может
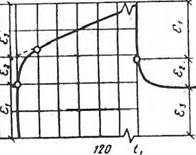
проявлять упругие, вязкоупругие и вязкие свойства. Для анализа деформаций материалов в температурном интервале, охватывающем эти три состояния, может быть использована модель, включающая три элемента: 1 - упругий; 2 - вязкоупругий; 3 - вязкий (рис. 1.22, а). Полная деформация этой модели равна сумме деформации каждого последовательно расположенного элемента:
Поскольку каждый элемент модели функционирует раздельно, он характеризуется своими значениями Е и г/, поэтому
£ = о/Е, + о/Е, (1 - elEy" : ) +at/r/3. (1.42)

На рис. 1.22, б представлено развитие деформации во времени. После прекращения действия напряжения, начиная с момента времени th упругая е, и вязкоупругая е: составляющие деформации становятся равными нулю, а вязкая деформация £ 3 необратима.
 60 время, с
Рис. 1.22. Модель вязкоупругости: а - модель деформаций; 1 - упругий элемент; 2 - вязкоупругий элемент (реологическое тело Кельвина'); 3 - вязкий элемент; б - реологическая кривая развития деформации во времени
60 время, с
Рис. 1.22. Модель вязкоупругости: а - модель деформаций; 1 - упругий элемент; 2 - вязкоупругий элемент (реологическое тело Кельвина'); 3 - вязкий элемент; б - реологическая кривая развития деформации во времени
|
Твердость, истираемость, износ
Твердостью называют свойство материала сопротивляться проникновению в него другого более твердого тела. Твердость
" У.Кельвин (1824-1907), лорд, титул, полученный английским физиком У.Томсоном за научные открытия.
природных каменных материалов оценивают шкалой Мооса, представленной десятью минералами, из которых каждый последующий своим острым концом царапает все предыдущие. Эта шкала включает минералы в порядке возрастающей твердости от 1 до 10:
1. Тальк Mg3 [Si40m][0H]2 - легко царапается ногтем.
2. Гипс CaS04-2H20 - царапается ногтем.
3. Кальцит СаСОз - легко царапается стальным ножом
4. Флюорит (плавиковый шпат) CaF2 - царапается стальным ножом под небольшим нажимом.
5. Апатит Cas [РО< |]з F - царапается ножом под сильным нажимом.
| 7. Кварц Si02 |
6. Ортоклаз K[AISij08] ] - легко царапают стекло,
применяются в качестве
8. Топаз Ah[Si40][F, 0H]2 ( абразивных (истирающих
9. Корунд АЬОз:. и шлифующих) материалов.
10. Алмаз С
Твердость древесины, металлов, бетона и некоторых других строительных материалов определяют, вдавливая в них стальной шарик или твердый наконечник (в виде конуса или пирамиды). В результате испытания вычисляют число твердости НВ = P/F, где F- площадь поверхности отпечатка.
От твердости материалов зависит их истираемость: чем выше твердость, тем меньше истираемость.
| (1.43) |
Истираемость оценивают потерей первоначальной массы образца материала, отнесенной к площади поверхности истирания и вычисляют по формуле (г/см2)
И = (т, - m: )/F,
где т, и т2 - масса образца до и после истирания.
Сопротивление материала истиранию определяют, пользуясь стандартными методами: кругом истирания и абразивами (кварцевыми песком и наждаком). Это свойство важно для эксплуатации дорог, полов, ступеней лестницы и т.п.
Износом называют свойство материала сопротивляться одновременному воздействию истирания и ударов. Износ определяют на образцах материалов, которые испытывают во вращающемся барабане со стальными шарами или без них. Показателем износа служит потеря массы пробы материала в результате проведенного испытания (в % от первоначальной массы).
Вопросы для самоконтроля
1. Какие существуют методы оценки для определения структуры материалов на микроуровне?
2. Какие числовые значения и размерности истинной и средней плотности, пористости, коэффициента плотности, теплопроводности и теплоемкости для тяжелого и ячеистого бетона, керамического кирпича и древесины?
3. Какие числовые значения прочности при сжатии, изгибе и растяжении с указанием размерности для тяжелого и ячеистого бетона, керамического кирпича и древесины?
4. Какие формы образцов и схемы испытаний используются для определения прочности материалов при сжатии, изгибе, растяжении?
5. Какие деформации в координатах напряжение-деформации показывают материалы упругие, пластичные, хрупкие?
6. Как можно моделировать механические свойства материалов?
Дополнительная литература
1. СивухинД.В. Общий курс физики. - М: Наука, 1979-1989, т. I-V.
2. Смирнов А.Ф. Сопротивление материалов. - М: Высшая школа, 1975.
3. Глинка Н.А. Общая химия. - JI.: Химия, 1985, 25-ое изд.
4. Рейнер М. Реология. - М., 1965.
5. Горшков В С. Методы физико-химического анализа вяжущих веществ. - М.: Высшая школа, 1981.
6. Горчаков В.И., Мурадов Э.Г. Основы стандартизации и управления качеством промышленности строительных материалов. - М., 1987.
7. Попов К.Н., Каддо М.Б., Кульков О.В. Оценка качества строительных материалов / Под ред. К.Н. Попова. - М., Изд-во АСВ, 1999
8. И.А. Рыбьев, Строительное материаловедение - М. Высшая школа, 2002
Глава II. ПОНЯТИЕ О КОМПОЗИЦИОННЫХ МАТЕРИАЛАХ
§ 1. Общие сведения
Композиционные материалы представляют собой гетерофаз- ные системы, получаемые из двух или более компонентов с сохранением индивидуальности каждого из них.
Один из компонентов, обладающий непрерывностью по всему объему, является матрицей. Другой компонент прерывный, разделенный в объеме композиции, считается упрочняющим или армирующим. Матричными материалами могут быть металлы, их сплавы, керамика, неорганические и органические вяжущие, полимеры. Упрочняющими компонентами чаще всего являются тонкодисперсные порошкообразные частицы или волокнистые материалы различной природы.
В композиционных материалах - композитах, разнородные компоненты создают синергетический эффект - новое качество материала, отличное от свойств исходных компонентов. В конструкционных композитах главное - это высокая удельная прочность (коэффициент конструктивного качества), превышающая аналогичную характеристику стали примерно в 15 раз.
Производство композитов в мире стремительно растет. В 1977 г. в Западной Европе и США было продано по 350 тыс. т композитов соответственно; в 1986 г. - уже по 1 млн. т, т.е. за 10 лет - утроение продукции. К 2000-2005 г.г. там ожидается годовое потребление композитов по 2, 5-3, 0 млн. т. Одновременно в передовых западных странах падает потребление стали. С учетом меньшей - в 4 раза массы, более высокого (в 2-3 раза) выхода при изготовлении готовых изделий, большей продолжительности эксплуатации (в 2-3 раза), 1, 0 т композита может заменить теоретически 15-25 т, а практически 4-5 т стали.
Появление названия композиционных материалов связано с принципиально новым направлением в технике, когда были созданы технологии, позволяющие получать высокопрочные материалы, в основном, для авиа-, ракето- и машиностроения. Примером такого материала, применяемого и в строительстве, являются стеклопластики, состоящие из полимерной матрицы и стекловолокон. Следовательно, дальнейшее создание новых материалов для строительства возможно будет развиваться с использованием теории и технологии композиционных материалов. Назовем их истинными композитами в отличие от других, к которым можно отнести многие строительные материалы: бетон, железобетон, фибробетон, асбестоцемент, древесностружечные, древесноволокнистые плиты и др.
§ 2. Состав и строение композита
Механические и другие свойства композита определяются тремя основными параметрами: высокой прочностью упрочняющих компонентов, жесткостью матрицы и прочностью связи на границе матрица-упрочнитель. Соотношение этих параметров характеризует весь комплекс механических свойств материала и механизм его разрушения. Работоспособность композита обеспечивается, как правильным выбором исходных компонентов, так и рациональной технологией производства, обеспечивающей сохранение их первоначальных свойств.
Многообразие упрочняющих и матричных материалов, а также схем армирования позволяет направленно регулировать прочность, жесткость, уровень рабочих температур и другие свойства путем подбора состава, изменения соотношения компонентов и др.
Для волокнистых композиционных материалов существует несколько классификаций, например, материаловедческий (по природе компонентов); конструктивный (по типу арматуры и ее ориентации в матрице). Можно выделить несколько больших групп композитов: с полимерной матрицей (пластики), с металлической матрицей (металлокомпозиты), с керамической матрицей и матрицей из углерода.
|
|