
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методы нахождения функций принадлежности
|
|
Из множеств методов нахождения функций принадлежности (ФП) НМ можно выделить две группы методов: прямые и косвенные.
В прямых методах эксперт или группа экспертов просто задают для каждого x Î X значение ФП. Как правило, прямые методы построения ФП используются для таких свойств, которые могут быть измерены по некоторой количественной шкале. Процесс задания ФП на основе некоторого количественного значения измеримого признака получил специальное название – фазификация (приведение к нечёткости). Поскольку абсолютная точность измерений является лишь удобной идеализацией для построения математических моделей, то фазификация более адекватно представляет объективно присутствующую неточность результатов физических измерений.
Для задания ФП может быть использована следующая процедура экспертного опроса. Если на вопрос о принадлежности элемента xi к НМ A L 1 экспертов из L экспертов отвечает положительно, то
 . (6.4)
. (6.4)
При прямых методах можно использовать и статистические данные наблюдения за объектом исследования. На основе статистических данных строится гистограмма той или иной неизвестной точно величины, которая и используется для задания ФП.
При использовании прямых методов построения ФП следует учитывать то обстоятельство, что не требуется абсолютно точного задания ФП, а достаточно фиксации лишь наиболее характерных её значений (например, для трапециевидной ФП – задание границ носителей и ядер).
Косвенные методы определения ФП используются в тех случаях, когда отсутствуют очевидные измерения свойства объекта исследования. При этом значения ФП должны удовлетворять заранее сформулированным условиям, а экспертные оценки являются исходными для их дальнейшей обработки. Дополнительные условия могут налагаться как на вид получаемой информации, так и на процедуру обработки.
Для конечных нечётких множеств среди косвенных методов нашёл широкое применение метод попарных сравнений, который основан на следующем предположении. Если бы значения искомой ФП были известны, то попарные сравнения элементов нечёткого множества A можно было бы представить в виде матрицы S с элементами  .
.
На практике вначале строят матрицу сравнений S, в которой  ,
,  , где n – число элементов НМ. Для определения элементов Sij можно использовать, например, шкалу относительной важности элемента НМ, приведённую в табл. 6.1.
, где n – число элементов НМ. Для определения элементов Sij можно использовать, например, шкалу относительной важности элемента НМ, приведённую в табл. 6.1.
Таблица 6.1.
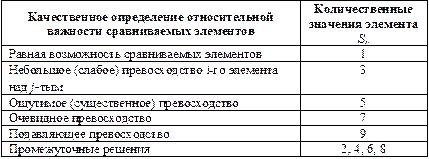
Построение функции принадлежности сводится к нахождению вектора W = ê w1, w2, …, w n ç, который является решением матричного уравнения
 , (6.5)
, (6.5)
где E – единичная матрица;
lmax – максимальное собственное число матрицы S;
T – означает транспонирование (вектор-строка превращается в вектор-столбец).
Вычисленные значения вектора W принимаются в качестве значений ФП:  . Поскольку все значения элементов матрицы S положительны по построению, то решение уравнения (6.5) существует и является положительным. Так как всегда выполняется равенство
. Поскольку все значения элементов матрицы S положительны по построению, то решение уравнения (6.5) существует и является положительным. Так как всегда выполняется равенство  , то величина отклонения lmax от n может служить мерой согласованности мнений экспертов. Количество вопросов к эксперту при данном методе равно
, то величина отклонения lmax от n может служить мерой согласованности мнений экспертов. Количество вопросов к эксперту при данном методе равно  , так как по определению
, так как по определению  а
а  . Из-за необходимости решать матричное уравнение данный метод является трудоёмким.
. Из-за необходимости решать матричное уравнение данный метод является трудоёмким.
Другим косвенным методом построения функции принадлежности, не требующим решения матричного уравнения, является метод ранговых оценок. Под рангом rij элемента xi Î X нечёткого множества A понимается число, характеризующее значимость этого элемента в формировании множества A. Естественно, что чем больше ранг элемента, тем больше значение его функции принадлежности. Предлагается выполнение условия
 . (6.6)
. (6.6)
Если добавить условие нормировки, например вида
 , (6.7)
, (6.7)
то значения ФП A (xi) легко находятся из уравнений (6.6) и (6.7):
 . (6.8)
. (6.8)
Выражение (6.8) даёт возможность определять ФП по абсолютным значениям рангов ri, которые могут определяться по 9-ти бальной шкале в соответствии с табл. 6.1.
Пример. Нечёткая переменная А состоит из пяти элементов xi Î Х, ранги которых по 9-ти бальной шкале равны: r 1 = 2; r 2 = 9; r 3 = 4; r 4 = 8;
r 5 = 6. Необходимо определить ФП нечёткой переменной A.
Решение. Используя метод ранговых оценок, в соответствии с (6.8) получаем: m1 = 0, 22; m2 = 1; m3 = 0, 44; m4 = 0, 89; m5 = 0, 67.
В заключение отметим, что с одной стороны одна и та же ФП может описывать качественно различные НМ, а с другой, – одно и то же НМ может быть представлено различными ФП, отражающими неоднозначность субъективных представлений о нём.
6.4. Операции над нечёткими множествами
Нечёткое множество является обобщением классического множества. Операции над НМ возможны тогда и только тогда, когда они определены на одном и том же универсальном множестве. Поскольку нечёткое множество полностью определяется своей ФП (она зачастую используется как синоним НМ), то операции над ним (НМ) – это операции над её ФП.
Ещё раз отметим, что ФП носит субъективный характер, хотя её часто и интерпретируют на основе понятий теории вероятностей. В рамках этой интерпретации m А (хi) для конечного НМ понимается как вероятность того, что ЛПР относят элемент хi к множеству А, а для бесконечного НМ m А (х) – это плотность распределения вероятностей. Так как в общем случае  – для конечных НМ, а
– для конечных НМ, а  – для бесконечных НМ, то для НМ требуется разработка своего математического аппарата, отличающегося от аппарата теории вероятностей, в которой указанная нормировка должна обязательно выполняться.
– для бесконечных НМ, то для НМ требуется разработка своего математического аппарата, отличающегося от аппарата теории вероятностей, в которой указанная нормировка должна обязательно выполняться.
Определим основные элементарные операции над НМ.
Равенство НМ. Нечёткие множества A и B считаются равными (A = B), если для всех х, принадлежащих универсальному множеству Х, выполняется условие
 . (6.9)
. (6.9)
Включение. Нечёткое множество  включает в себя НМ B (B Í A), если
включает в себя НМ B (B Í A), если
 . (6.10)
. (6.10)
При этом говорят, что НМ A доминирует над НМ B или НМ A содержит в себе НМ B.
Пересечением двух НМ A и B называется НМ C (C = A Ç B), заданное на том же универсальном множестве Х, функция принадлежности которого
 . (6.11)
. (6.11)
В математической логике операция пересечения соответствует логической операции “И”.
Пример 1. Пусть А – НМ “Актив с небольшой доходностью”:

а В – НМ “Актив с доходностью, примерно равной 5”:

Найти нечёткое множество С “Актив с небольшой доходностью, примерно равной 5”.
Решение. Так как (C = A Ç B), то в соответствии с (6.11) получаем:

Результат операции пересечения двух бесконечных НМ показан на рис.6.5.
Объединением двух НМ A и B называется НМ C (C = A È B), заданное на том же универсальном множестве X, функция принадлежности которого
 (6.12)
(6.12)
Результат объединения НМ показан на рис. 6.6.

Рис. 6.5. Функция принадлежности НМ C = A Ç B
Операция объединения НМ соответствует логической операции “ИЛИ”.

Рис. 6.6. Функция принадлежности НМ C = A È B
Разностью НМ A и НМ B называется НМ C (C = A - B), заданное на одном и том же универсальном множестве X, функция принадлежности которого
 (6.13)
(6.13)
Функция принадлежности разности НМ показана на рис. 6.7.
Дополнением НМ A называется нечёткое множество  , функция принадлежности которого
, функция принадлежности которого
 . (6.14)
. (6.14)
Результат дополнения показан на рис. 6.8.

Рис. 6.7. Функция принадлежности НМ С = А - В

Рис. 6.8. Функция принадлежности НМ 
Операция дополнения соответствует логической операции “НЕ”. Содержательно, если  – НМ “Актив с небольшой доходностью”, то
– НМ “Актив с небольшой доходностью”, то  – “Актив с большой доходностью”.
– “Актив с большой доходностью”.
Из указанных определений операций над НМ следует, что  Ø =
Ø =  ;
;  Ø = Ø;
Ø = Ø;  ;
;  , где Ø – пустое множество.
, где Ø – пустое множество.
Особенностью рассматриваемых операций над НМ является то, что для них  ¹ Ø,
¹ Ø,  ¹ Х.
¹ Х.
Если  – произвольные НМ, заданные на одном и том же универсальном множестве Х, операции над ними обладают следующими свойствами.
– произвольные НМ, заданные на одном и том же универсальном множестве Х, операции над ними обладают следующими свойствами.
1. Коммутативность операций объединения и пересечения НМ:
 .
.
2. Ассоциативность операций объединения и пересечения НМ:

3. Дистрибутивность операций объединения и пересечения НМ относительно друг друга:

4. Идемпотентность операций объединения и пересечения НМ:

5. Поглощение одного из НМ при операциях объединения и пересечения:

6. Инволюция (двойное дополнение) НМ:

7. Закон де Моргана:

Рассмотренные операции широко используются для задач нечёткого моделирования, и они по своему смыслу в максимальной степени приближаются к булевой алгебре. Вместе с тем приведённые определения этих операций не единственны.
Над нечёткими интервалами и числами, являющимися частным случаем нечётких величин, можно выполнять все четыре арифметические операции: сложение; вычитание; умножение и деление. Обозначим любую из этих операций знаком  . Для нахождения нечёткой величины
. Для нахождения нечёткой величины  необходимо по известным ФП
необходимо по известным ФП  и
и  найти ФП
найти ФП  .
.
Для этого требуется использовать принцип обобщения, который имеет вид:
 (6.15)
(6.15)
Здесь  следует понимать таким образом, что носитель нечёткой величины
следует понимать таким образом, что носитель нечёткой величины  получается путём выполнения соответствующей арифметической операции над всеми значениями, входящими в носители нечётких величин А и В.
получается путём выполнения соответствующей арифметической операции над всеми значениями, входящими в носители нечётких величин А и В.
хС Î SC располагают в порядке возрастания со значениями функции принадлежности, равной

Отметим, что для нечётких величин, в отличие от чётких:
А – А ¹ 0; А / А ¹ 1.
Пример. Даны два дискретных нечётких числа:
 .
.
Для простоты НЧ будем записывать и в таком виде:  , где в числителе стоит
, где в числителе стоит  , а в знаменателе
, а в знаменателе  . Необходимо найти НЧ
. Необходимо найти НЧ  .
.
Решение. В соответствии с принципом обобщения (6.15) над любыми числами, входящими в носитель  НЧ А и в носитель
НЧ А и в носитель  НЧ В, выполняем соответствующую арифметическую операцию. Результату этой операции присваиваем значение ФП, равное
НЧ В, выполняем соответствующую арифметическую операцию. Результату этой операции присваиваем значение ФП, равное  , т.е. минимальное из двух значений ФП.
, т.е. минимальное из двух значений ФП.
Если в результате выполнения соответствующей арифметической операции над всеми числами, входящими в  и
и  , какое-то число получилось более одного раза, то ему присваивают значение ФП максимальное из всех полученных ранее минимальных значений, т.е. выполняют операцию
, какое-то число получилось более одного раза, то ему присваивают значение ФП максимальное из всех полученных ранее минимальных значений, т.е. выполняют операцию  .
.
Таким образом, получаем:




Пример арифметических операций над непрерывными НЧ показан на рис.6.9.
При использовании трапециевидных ФП результаты арифметических операций над нечёткими интервалами получаются следующим образом:
 (6.16)
(6.16)
 (6.17)
(6.17)
 ; (6.18)
; (6.18)
 (6.19)
(6.19)
где НЧ 

Рис. 6.9. Функции принадлежности результатов арифметических операций над НЧ
Примечание. Операция деления нечёткой величины  на нечёткую величину
на нечёткую величину  определена только для случая, если в носитель
определена только для случая, если в носитель  не входит ноль. В противном случае эта операция не определена.
не входит ноль. В противном случае эта операция не определена.
Пример. Как известно, точка безубыточности находится из уравнения  . Пусть А – минимально-допустимая чистая прибыль; Р – цена единицы выпускаемого товара (услуги); С – постоянные издержки и В – переменные издержки на единицу продукции являются нечёткими величинами с трапециевидными ФП вида:
. Пусть А – минимально-допустимая чистая прибыль; Р – цена единицы выпускаемого товара (услуги); С – постоянные издержки и В – переменные издержки на единицу продукции являются нечёткими величинами с трапециевидными ФП вида:
 .
.
Найти точку безубыточности.
Решение. Точка безубыточности 
Так как носитель знаменателя  содержит ноль, то операция деления не выполнима.
содержит ноль, то операция деления не выполнима.
Пусть  . В этом случае:
. В этом случае:

6.5. Сравнение нечётких величин
Если пересечение носителей двух нечётких величин  и
и  не пусто
не пусто  Ø), вопрос “Какая из этих двух величин больше? ” не является простым.
Ø), вопрос “Какая из этих двух величин больше? ” не является простым.
Действительно, пусть при первой реализации значения нечётких величин  и
и  оказались равными
оказались равными  и
и  , а во второй реализации равными оказались значения
, а во второй реализации равными оказались значения  и
и  (рис.6.10), тогда в первом случае
(рис.6.10), тогда в первом случае  , а во втором –
, а во втором – 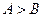 .
.

Рис. 6.10. Сравнение нечётких величин А и В
Таким образом, в общем случае отношения строгого порядка > или < на множестве нечётких величин являются нечёткими и лишь в случае, когда  Ø, эти отношения между нечёткими величинами будут строгими.
Ø, эти отношения между нечёткими величинами будут строгими.
Для сравнения нечётких величин используется ряд индексов ранжирования (сравнения), которые должны быть некоторой чёткой функцией  от нечётких аргументов. Значение индекса ранжирования для каждой пары нечётких величин должно показывать, какая из двух нечётких величин
от нечётких аргументов. Значение индекса ранжирования для каждой пары нечётких величин должно показывать, какая из двух нечётких величин  и
и  больше (меньше) и во сколько раз. Если
больше (меньше) и во сколько раз. Если  , то
, то 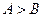 в
в  раз, в противном случае
раз, в противном случае  .
.
Рассмотрим некоторые из возможных индексов ранжирования для нормальных нечётких величин.
Индекс ранжирования  определяется следующим образом: если
определяется следующим образом: если  , то
, то
 , (6.20)
, (6.20)
причём, если  , то
, то 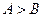 , в противном случае
, в противном случае  .
.
Пример. Сравнить  и
и  , ФП которых показаны на рис.6.11.
, ФП которых показаны на рис.6.11.

Рис. 6.11. Определение индекса ранжирования Н 1(А, В)
Решение. Для рассматриваемого примера из рис. 6.11 получаем, что

Точное значение  можно найти из решения алгебраического уравнения, левая и правая части которого описывают соответствующие ветви ФП нечётких величин
можно найти из решения алгебраического уравнения, левая и правая части которого описывают соответствующие ветви ФП нечётких величин  и
и  . Находим значение
. Находим значение  , которое соответствует точке пересечения этих ветвей:
, которое соответствует точке пересечения этих ветвей:  Откуда
Откуда 
Подставляя это значение в соответствующие уравнения пересекающихся ветвей ФП, получаем: 
Так как  то Н 1 = Н (А, В) = 0, 875, т.е.
то Н 1 = Н (А, В) = 0, 875, т.е.  .
.
Индекс ранжирования  определяем следующим образом:
определяем следующим образом:
 , (6.21)
, (6.21)
где
 (6.22)
(6.22)
 и
и  –
–  -срезы нечётких величин
-срезы нечётких величин  и
и  соответственно.
соответственно.
По индексу ранжирования  большим считается та нечёткая величина, у которой координата середины
большим считается та нечёткая величина, у которой координата середины  -среза больше (рис.6.12).
-среза больше (рис.6.12).
Легко показать, что для трапециевидных ФП индекс ранжирования  можно рассчитывать по формуле
можно рассчитывать по формуле
 , (6.23)
, (6.23)
где НЧ  с трапециевидной ФП определяется числами
с трапециевидной ФП определяется числами  , а НЧ
, а НЧ  .
.

Рис. 6.12. Определение индекса ранжирования Н 2(А, В)
Для случая  индекс ранжирования
индекс ранжирования  сводится к оценке интервалов, соответствующих ядрам НЧ
сводится к оценке интервалов, соответствующих ядрам НЧ  и
и  , а при
, а при  – оценке интервалов, соответствующих носителям чисел
– оценке интервалов, соответствующих носителям чисел  и
и  . На практике обычно берут
. На практике обычно берут  .
.
При  получаем:
получаем:
 . (6.24)
. (6.24)
Для рассматриваемого примера (рис. 6.11) и a = 0, 6 получаем:
 ,
,
то есть  немного меньше В.
немного меньше В.
Используется также интегральный от  индекс ранжирования
индекс ранжирования  :
:
 . (6.25)
. (6.25)
Для трапециевидных ФП индекс ранжирования  принимает простой для расчётов вид:
принимает простой для расчётов вид:
 . (6.26)
. (6.26)
Как видим, в том случае  совпадает с индексом
совпадает с индексом  для случая, когда a-срез берётся на уровне a = 0, 5.
для случая, когда a-срез берётся на уровне a = 0, 5.
Для нечётких величин, представленных на рис. 6.11, получаем:
 .
.
Индекс ранжирования  равен
равен
 , (6.27)
, (6.27)
где  и
и  – аргументы носителей величин А и В соответственно, делящие их ФП на равные по площади части, то есть:
– аргументы носителей величин А и В соответственно, делящие их ФП на равные по площади части, то есть:
 (6.28)
(6.28)
 . (6.29)
. (6.29)
Для рассматриваемого выше примера, чтобы определить  и
и  , вначале определим площадь под ФП нечётких величин
, вначале определим площадь под ФП нечётких величин  и
и  :
:


Далее определяем координаты  и
и  , делящие эти площади на равные части:
, делящие эти площади на равные части:

Из этих уравнений получаем  . Тогда
. Тогда  Следовательно по индексу ранжирования
Следовательно по индексу ранжирования 
 чуть-чуть больше
чуть-чуть больше  .
.
Лица, принимающие решения, которые не склонны к риску, могут использовать индекс ранжирования  , который для случая
, который для случая  имеет вид
имеет вид
 . (6.30)
. (6.30)
По этому индексу большей считается та нечёткая величина, у которой аргумент  правой части ядра больше (ранжирование по правому модальному значению ФП). Для
правой части ядра больше (ранжирование по правому модальному значению ФП). Для  и
и  , представленных на рис. 6.11, имеем:
, представленных на рис. 6.11, имеем:

Индекс ранжирования  равен:
равен:
 , (6.31)
, (6.31)
где  и
и  – координаты центра тяжести ФП нечётких величин
– координаты центра тяжести ФП нечётких величин  и
и  соответственно.
соответственно.
Координата центра тяжести вычисляется по формуле
 . (6.32)
. (6.32)
Для рассматриваемого примера (рис.6.11) получаем, что:

 ;
;

Следовательно, 
В табл. 6.2 приведены значения различных индексов ранжирования для нечётких величин с различными ФП.
Таблица 6.2
| Нечёткие числа | Индексы ранжирования | |||||||||||||||||
| Н 1 | Н 2 | 
| Н 3 | Н 4 | Н 5 | |||||||||||||
| a=1 | a=0, 8 | a=0, 2 | ||||||||||||||||

| 0, 67 | 0, 5 | 0, 57 | 0, 87 | 0, 71 | 0, 5 | 0, 8 | 0, 8 | ||||||||||

| ||||||||||||||||||

| 0, 85 | 0, 6 | 0, 67 | 0, 81 | 0, 86 | 0, 8 | ||||||||||||
| Нечёткие числа | Индексы ранжирования | |||||||||||||||||
| Н 1 | Н 2 | 
| Н 3 | Н 4 | Н 5 | |||||||||||||
| a=1 | a=0, 8 | a=0, 2 | ||||||||||||||||

| 0, 83 | 0, 75 | 0, 84 | 1, 19 | 0, 73 | 0, 75 | 1, 06 | |||||||||||

| 0, 875 | 0, 556 | 0, 67 | 1, 12 | 0, 87 | 0, 87 | 0, 6 | 0, 96 | ||||||||||
Сравнительная оценка результатов ранжирования нечётких величин, приведённых в табл. 6.2, показывает, что индексы ранжирования  и
и  при
при  одинаково проранжировали нечёткие величины, хотя их значения, характеризующие степень отличия, и не совпадают.
одинаково проранжировали нечёткие величины, хотя их значения, характеризующие степень отличия, и не совпадают.
Существенные отличия даёт индекс ранжирования  при малых уровнях a-среза. В этом случае, по существу, производится интервальная оценка носителей нечётких величин.
при малых уровнях a-среза. В этом случае, по существу, производится интервальная оценка носителей нечётких величин.
Индекс  имеет во всех приведённых примерах большие значения, чем другие индексы.
имеет во всех приведённых примерах большие значения, чем другие индексы.
В соответствии с рекомендациями прикладного системного анализа совпадение результатов ранжирования, полученных по различным индексам, даёт ЛПР большую степень уверенности в правильности принимаемого решения.
Расчёт всех индексов ранжирования, по существу, состоит из двух этапов: на первом этапе каждому нечёткому числу ставят в соответствие чёткое число, например, А a+ + А a-; х 0 А ; х ц.т. А ; max(arg maxm A (x)). Этот этап называется дефазификацией (приведение к чёткости). На втором этапе производится сравнение уже чётких величин, полученных в результате дефазификации.
Дефазификация используется не только, когда требуется сравнивать нечёткие величины, но и в нечётких системах принятия решений, в задачах распознавания и других.
Действительно, поскольку в системах управления исполнительные устройства должны получать команды в виде точных, конкретных значений, то необходимо преобразовывать нечёткую информацию в точные значения управляющих сигналов.
Наиболее часто для дефазификации используют метод определения центра площади ФП, как в индексе ранжирования  , или метод центра тяжести, как в индексе ранжирования
, или метод центра тяжести, как в индексе ранжирования  .
.
Пример. Дефазификация.
Пусть необходимая сумма наличных долларов в пункте обмена в начале рабочего дня, как показывает опыт, является нечёткой величиной  с ФП вида: А = á 1; 2; 3; 4; 5ñ.
с ФП вида: А = á 1; 2; 3; 4; 5ñ.
Необходимо решить, какую сумму долларов завести в данный пункт обмена (произвести дефазификацию НЧ А).
Решение. Если проводить дефазификацию по методу определения центра тяжести ФП  , то получаем:
, то получаем:

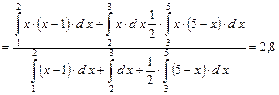 .
.
Таким образом, в пункт обмена следует завезти $ 2, 8 тыс.
Если проводить дефазификацию по методу центра площади ФП  , то
, то  определяется из уравнения
определяется из уравнения
 .
.
Так как  , то
, то  Тогда
Тогда  или
или  .
.
Как видим, отличие результатов дефазификации по двум методам несущественно (результаты отличаются на  ).
).
6.6. Сравнение конечных нечётких множеств
Пусть требуется сравнить два нечётких множества  и
и  , заданных на конечном универсуме
, заданных на конечном универсуме 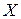 . Измерение частичного совпадения множеств
. Измерение частичного совпадения множеств  и
и  сводятся к оценке их пересечения
сводятся к оценке их пересечения  ; измерение несовпадения – к оценке пересечения
; измерение несовпадения – к оценке пересечения  или
или  , а измерение сходства – к оценке разности
, а измерение сходства – к оценке разности  . Соответствующие индексы сравнения определяются как функции мощности нечётких множеств
. Соответствующие индексы сравнения определяются как функции мощности нечётких множеств  ;
;  и
и  . Обобщённый индекс сравнения имеет вид:
. Обобщённый индекс сравнения имеет вид:
 , (6.33)
, (6.33)
где * – операции над НМ;
g – скалярная функция нечёткого множества;
f – операция, обеспечивающая нормализацию скалярной функции.
Скалярная функция есть отображение всех нечётких множеств в значения  , отвечающее условиям
, отвечающее условиям  (Ø) = 0;
(Ø) = 0;  (Х) = 1;
(Х) = 1;  , если
, если  . Индексы сравнения имеют следующие свойства:
. Индексы сравнения имеют следующие свойства:
1) если  Ø,
Ø,  ;
;
2) если  .
.
В качестве индекса несовпадения НМ  и
и  может быть величина
может быть величина
 (6.34)
(6.34)
где  – означает скалярную мощность нечёткого множества:
– означает скалярную мощность нечёткого множества:
 (6.35)
(6.35)
Заметим, что  , как правило, не равняется
, как правило, не равняется  . Это свойство может использоваться для определения, какое из конечных нечётких величин больше. Если
. Это свойство может использоваться для определения, какое из конечных нечётких величин больше. Если  , то
, то  . В качестве индекса совпадения НМ
. В качестве индекса совпадения НМ  и
и  может быть величина
может быть величина
 . (6.36)
. (6.36)
Очевидно, что  .
.
Наконец, в качестве индекса сходства может быть взята величина
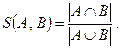 (6.37)
(6.37)
Заметим, что индексы  и
и  отражают различную информацию о нечётких множествах и поэтому сходство и отрицание несходства не будут точными синонимами.
отражают различную информацию о нечётких множествах и поэтому сходство и отрицание несходства не будут точными синонимами.
Для этого индекса также справедливо свойство 
Пример. Пусть имеется два рынка продажи хороших автомобилей.
Первый рынок определяется НМ
 ,
,
а второй рынок НМ
 .
.
Требуется сравнить эти два рынка.
Решение. Индекс несовпадения НМ A и B:

Индекс совпадения НМ  и
и  :
:

Индекс сходства:
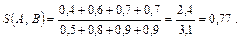
6.7. Нечёткие отношения
Понятия нечёткого отношения, как и само понятие нечёткого множества, относятся к фундаментальным основам теории нечётких множеств.
Нечётким отношением Q называется некоторое фиксированное нечёткое подмножество, заданное на декартовом произведении множеств (универсумов) Х 1 ´ Х 2 ´ … ´ Хп своей функцией принадлежности m q Î [0, 1].
Если нечёткое отношение Q задаётся на декартовом произведении двух множеств (универсумов) Х ´ Y, то оно называется бинарным, а в общем случае - k -нарным нечётким отношением.
Функция принадлежности m q (Х , Y) нечёткого бинарного отношения определяет степень зависимости между х Î Х и
y Î Y. Например, в случае нечёткой системы управления нечёткое отношение Q можно трактовать, как описание нечёткой реакции этой системы на каждое входное управление хi Î Х (рис. 6.13).

Рис. 6.13. Интерпретация нечёткого отношения как реакции нечёткой системы управления
Таким образом, на каждое воздействие хi Î Х на выходе нечёткой системы управления можно получить любой отклик yj Î Y, но с разной возможностью, которая определяется значением функции принадлежности m i (yj).
Бинарное нечёткое отношение называется нечёткимотображением, если для любого элемента хi Î Х существует не более одного элемента yj Î Y с отличным от нуля значением функции принадлежности.
Если в качестве универсумов X и Y рассматриваются числовые множества, то соответствующее нечёткое отображение называется нечёткойфункцией.
Нечёткая алгебраическая операция является частным случаем нечёткого отношения, когда все универсумы
Х 1, Х 2, …, Хп тождественно равны X.
Для нахождения реакции (отклика) нечёткого отношения на нечёткое входное множество (в частном случае, значение нечёткой функции от нечёткого аргумента) необходимо использовать принцип обобщения.
Принцип обобщения позволяет ответить на вопрос, какое нечёткое множество B в Y следует поставить в соответствие нечёткому множеству A Î X если известно нечёткое отношение предпочтения Q.
Принцип обобщения. Образом  нечёткого множества A в X при нечётком отношении Q (m q Î (x, y)) является нечёткое множество B с функцией принадлежности
нечёткого множества A в X при нечётком отношении Q (m q Î (x, y)) является нечёткое множество B с функцией принадлежности
 . (6.38)
. (6.38)
Как следует из (6.38) в основе этого определения лежит максиминная композиция функций принадлежности m A (x) и m q (x, y).
В частном случае, когда Q - чёткое отображение
y = j(x), то определение (6.38) приобретает вид:
 . (6.39)
. (6.39)
Нечёткие отношения могут задаваться различными способами: в виде матрицы нечёткого отношения; в виде нечётких графов; аналитически в форме некоторых математических функций.
Пример. Пусть НМ A имеет вид: A = á (x 1/0, 2); (x 2/0, 5); (x 3/1); (x 4/0, 6)ñ а нечёткое бинарное отношение Q имеет вид ФП m q (x, y), которая задана следующей матрицей:
 .
.
Требуется найти образ B нечёткого множества A в Y, отображаемый нечётким отношением Q.
Решение. В соответствии с принципом обобщения (6.38) вначале берётся операция минимума для всех элементов строки m A (x) и столбца m q (x, yj), а затем для полученных результатов берётся операция максимума (для данной задачи операция sup (нахождение точной верхней границы) эквивалентна операции max):


Таким образом, B = á (y 1/0, 5); (y 2/1); (y 3/0, 5)ñ.
Рассмотрим нечёткое отношение, которое содержательно описывает выбор рыночной стратегии. Пусть универсальное множество X состоит из трёх элементов характеризующих рынки сбыта: x 1 - имеющийся хорошо известный рынок сбыта; x 2 - новый рынок, связанный с имеющимся рынком; x 3 - совершенно новый рынок сбыта. Универсальное множество Y также содержит три элемента: y 1 - товары, выпускаемые в настоящее время; y 2 – новые товары, связанные по характеру со старыми товарами; y 3 - совершенно новые товары.
Нечёткое отношение, которое характеризует модель “Рынок/Товары”, представим в виде следующего нечёткого графа (рис. 6.14).

Рис. 6.14. Нечёткий граф отношения Q, характеризующий модель “Рынок/Товары”
Значения функций принадлежности m q (xi, yj) количественно описывают степень уверенности в успешной продаже товаров на том или ином рынке. Они заданы на основе субъективных оценок менеджера, и исходят из известного правила, что продавать существующий ассортимент товаров или услуг проще тем покупателям, которые уже их покупали, а осваивать новые рынки сбыта сложнее.
Пример. Пусть рынки сбыта характеризуются нечётким множеством A = á (x 1/0, 8); (x 2/1); (x 3/0, 3)ñ. Используя нечёткое отношение Q для модели “Рынок/Товары”, представленное нечётким графом на рис. 6.14 требуется найти образ B нечёткого множества “Выпускаемые товары”.
Решение. В соответствии с принципом обобщения:



Ответ. B = á (y 1/0, 8); (y 2/0, 9); (y 3/0, 5)ñ, то есть наименее рекомендуемыми для производства являются совершенно новые товары.
Рассмотрим еще один случай, когда нечёткое множество А непрерывно. В этом случае и отношение предпочтения также представляет собой непрерывную функцию. Вновь требуется найти нечёткое множество В.
Решение данной задачи покажем на следующем примере [16].
Пример. Нечёткое множество А имеет функцию принадлежности  , k 1 > 0, x ³ 0. Нечёткое отношение j имеет функцию принадлежности
, k 1 > 0, x ³ 0. Нечёткое отношение j имеет функцию принадлежности  , k 2 > k 1 (рис. 6.15).
, k 2 > k 1 (рис. 6.15).
Требуется найти нечёткое множество В, индуцируемое нечётким отношением j
Решение. В соответствии с принципом обобщения вначале найдем  .
.
Как видно из рис.6.15. кривые m А (х) и mj(x, y) пересекаются в двух точках, в которых
а)  при 0 £ х £ y;
при 0 £ х £ y;
б)  при х ³ y.
при х ³ y.

Рис. 6.14. К определению нечёткой функции от нечёткого аргумента
Первая точка соответствует 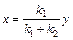 , а вторая -
, а вторая -  .
.
Максимум минимума (m А (х), mj(х, y)) достигается в точке  .
.
Подставляя это значение в выражение mj(х, y), получаем  .
.
Нечёткие отношения имеют такие же характеристики, что и нечёткие множества: носитель; ядро; a-срез. И над ними можно выполнять операции пересечения, объединения, разности, дополнения.
Нечёткое отношение Q строго доминирует нечёткое отношение G (записывается G Ì Q), если значения функции принадлежности первого отношения строго больше соответствующих значений ФП второго.
Если нечёткое бинарное отношение R задано на декартовом произведении универсумов X 1 и X 2, а нечёткое бинарное отношение Q на декартовом произведении универсумов X 1 ´ X 3, то нечёткое бинарное отношение, заданное на декартовом произведении X 1 ´ X 3 с функцией принадлежности  , называется композицией двух бинарных нечётких отношений.
, называется композицией двух бинарных нечётких отношений.
Из определения операции композиции следует, что она ассоциативна, то есть
R × (Q × P) = (R × Q) × P. (6.40)
Пример. Пусть бинарные нечёткие отношения R и Q имеют, соответственно, матрицы ФП вида:
 ,
,
 .
.
Найти композицию R × Q нечётких отношений.
Решение. В соответствии с максиминной свёрткой (6.40) получаем:

Бинарное нечёткое отношение, заданное на одном универсуме X, определяется как нечёткое отношение Q, функция принадлежности которого m q (xi, xj) Î [0, 1], где xi Î X и xj Î X.
Пример. Пусть универсум X состоит из 5 натуральных чисел: X = [1; 2; 3; 4; 5], а Q описывает свойство “натуральное число xi Î X приближённо равно натуральному числу xj Î X ”.
Тогда бинарное нечёткое отношение на одном универсуме X может иметь следующую функцию принадлежности:
 .
.
Бинарное нечёткое отношение, заданное на одном универсуме X, может обладать такими свойствами как:
Рефлексивность: m q (xi, xj) = 1; " xi Î X (главная диагональ матрицы m Rq (xi, xj) имеет элементы, равные единице).
Симметричность: m q (xi, xj) = m q (xj, xi), " xi, xj Î X (элементы матрицы m q (xi, xj) симметричны относительно главной диагонали).
Контранзитивность: m q (xi, xj) ³ min max
m q (xi, xj) ³ min max (m q (xi, xj), m q (xi, xj)), " хi, хj, хR Î X (при увеличении разности ê хi + хj ç ФП m q (xi, xj) монотонно уменьшается).
Пример. Пусть универсум X = [ x 1, x 2, x 3, x 4] - некоторая совокупность людей. На этом универсуме задано бинарное нечёткое отношение Q, отражающее степень знакомства этих людей. Очевидно, что это нечёткое отношение обладает свойствами рефлективности и симметричности, однако свойством контранзитивности в общем случае не обладает.
Пусть  .
.
Нас интересует возможность передачи информации (например, о возможном банкротстве банка) среди рассматриваемой совокупности людей. Эта задача может быть решена путём применения операции транзитивного замыкания бинарного нечёткого отношения, результатом которого является матрица
 , (6.41)
, (6.41)
где п - размерность матрицы М, а знак È означает операцию объединения.
В рассматриваемом примере п = 4.
Для получения матрицы транзитивного замыкания МТ.З., используя последовательно максиминную композицию двух бинарных нечётких отношений, найдём матрицы:
 ;
;
 .
.
Таким образом, матрица транзитивного замыкания равна:
 .
.
Заметим, что в нашем примере М 3 = М 4. Оказывается, то это свойство носит общий характер: если для некоторого натурального числа k (1 £ k £ n) М k = М k -1, то дальнейшие расчёты степеней композиции М k -1 выполнять не надо, а матрица транзитивного замыкания нечёткого отношения будет равна:
 . (6.42)
. (6.42)
Анализ полученной в примере матрицы МТ.З показывает, что информация достаточно быстро распространяется среди всех без исключения людей рассм
|
|