Аналитическое исследование СМО с конечным числом состояний.

Порядок выполнения работы.

1. Ознакомиться с методическими указаниями.
2. Для одноканальной СМО с одним местом ожидания в очереди (типа М/М/I) аналитическим методом рассчитать вероятность того, что к моменту t в системе будет ровно k требований. Обозначить эту вероятность P_k(t). Аналогичные расчеты провести численным методом на ЭВМ и оценить достигнутую точность численного метода.
3. Для заданного варианта СМО исследовать зависимость длительности переходного процесса в СМО от его параметров. При расчетах принять в качестве времени окончания переходного процесса в системе время, за которое все реализации Pk(t) вошли в 5%-ую трубку от установившегося состояния.
4. построить графики, на которых изобразить результаты, полученные в пп. 2 и 3.
5. Рассчитать на ЭВМ математическое ожидание числа занятых каналов и среднюю длину очереди в переходном режиме и сравнить результаты с аналогичными значениями в установившемся режиме.
6. Оформить отчет, в котором привести результаты машинного и ручного счета, графики.
7. Ответить на контрольные вопросы.

Основные положения.

Аналитическое исследование СМО с конечным числом состояний.

Имеется n-канальная СМО, на вход которой поступает простейший поток требований с интенсивностью λ. Время обслуживания в каждом канале распределено по экспоненциальному закону с параметром μ (интенсивность процесса обслуживания). Максимальная длина очереди ограничена числом m. Если хотя один канал свободен, то пришедшее требование сразу поступает на обслуживание.

Когда каналы заняты, пришедшее требование становится в очередь. Если же в очереди уже находятся m требований, то пришедшее требование получает отказ в обслуживании и покидает систему. Происходит потеря требования.

Обозначим K(t)-число требований, находящихся в СМО в момент времени t. Для описания процесса K(t) необходимо знать вероятности Pk(t)=P{K(t)=k}, где 0≤ k≤ n+m.

В данной системе процесс K(t) можно рассматривать как процесс размножения и гибели. В результате вероятности состояний системы описываются следующими уравнениями [1]:

Исследуемая СМО имеет конечное число состояний и, следовательно, при достаточно длительном функционировании должна входить в режим статистического равновесия. Этот режим, как известно, характеризуется стационарным распределением вероятностей, не зависящим от начальных условий: для всех k=0, 1, …, n+m.

Для тех СМО, период функционирования которых столь велик, что большую его часть они находятся в состоянии статистического равновесия, бывает достаточно ограничиться стационарным распределением вероятностей и, исходя из него, вычислить все показатели эффективности СМО. Однако поведение многих СМО представляет интерес в период, непосредственно следующий за началом функционирования (в частности, тех СМО, период функционирования которых невелик). Для таких систем необходимо изучение их в нестационарном режиме, предшествующем режиму статистического равновесия. Кроме того, обосновано ограничиться исследованием только режима статистического равновесия можно лишь в том случае, если известно, когда он наступает. Для этого также необходимо изучение нестационарного режима.

Анализ нестационарного режима можно провести, решив систему (1.1). Ее удобно решать с помощью преобразований Лапласа. Обозначим

В качестве начальных условий примем

Применяя преобразования Лапласа к системе (1.1) и учитывая, что

имеем

Система (1.4) содержит n+m+1 алгебраических уравнений. Она может быть разрешена с использованием правил Крамера:

,

где D(s) – главный определитель системы (1.4); D_k(s) – присоединенный определитель, полученный из главного определителя D(s) путем замены его k-го столбца (т.е. столбца, состоящего из коэффициентов при искомом изображении P_k(s)) столбцом, состоящим из правых частей системы (1.4).

Главный определитель системы D(s) можно вычислить, используя рекуррентную процедуру последовательного разложения определителя по столбцам и строкам.

Как известно, наибольшие трудности применения такого метода решения системы дифференциальных уравнений заключены в отыскания оригинала по изображению. Эта задача упрощается в связи с тем, что изображение (1.5) имеет дробно-рациональную форму. Можно показать [2], что обратное преобразование Лапласа для данной задачи имеет вид:

где S_i - значение i-го корня полинома D_I(s).

D_I(s) находится из соотношения D(s)=SD_I(S).

Учитывая, что при S®0 имеет место t®¥, а также, что S_k< 0 для всех k=1, 2,..., n+m, первое слагаемое выражения (1.5) можно трактовать следующим образом:

Это означает, что первое слагаемое в формуле для P_k(t) отвечает финальной вероятности P_k, а второе - описывает изменение вероятности P_k(t) в нестационарном режиме.

Полином D_I, корни которого надо найти, имеет порядок n+m. Следовательно, в большинстве практических случаев аналитическое исследование нестационарного режима описанным методом сопряжено с решением алгебраических уравнений высокого порядка. В этих случаях наиболее употребительным способом поиска корней является метод итераций (последовательных приближений).

На основании сказанного можно сделать вывод, что аналитическое исследование нестационарного режима в многоканальных СМО чрезвычайно трудоемко, а в случаях, когда число каналов и мест в очереди достаточно велико, в силу технических трудностей не может осуществиться без применения вычислительной техники.

Поэтому при решении задач такого рода наряду с аналитическими (а иногда и вместо них) необходимо пользоваться и численными методами исследования.

Пример. Рассмотрим одноканальную систему с одним местом ожидания (n = 1, m = 1). Уравнения для вероятностей состояний такой системы имеют вид

Преобразование Лапласа приводит к системе трех алгебраических уравнений:

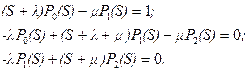
Определитель системы

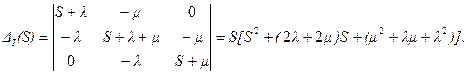
Приравнивая D(s) к нулю, находим полюса изображения P_k(s), k=0, 1, 2:

Так как l> 0 и m> 0, то S₁ и S₂ отрицательны и различны. Теперь вычислим присоединенные определители D_k(s):

Согласно правилу Крамера имеем

Для определения оригинала необходимо вычислить производную выражения, стоящего в знаменателе в квадратных скобках.

Имеем

Запись выражений для оригиналов P_k(t) в общем случае громоздка, хотя принципиально легко выполнима. Поэтому вычислим вероятность P_k(t) для конкретных значений l и m. Однако предварительно проверим правильность полученных выражений. Отношение полиномов D_k(0)/D_I(0) представляет собой вероятность k-го состояния в режиме статистического равновесия, т.е. финальную вероят­ность P_k(¥)=P_k. Эти вероятности должны отвечать нормирующему условию . Кроме того, как следует из анализа стационарного режима, для них должны выполняться соотношения

Имеем

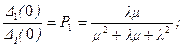
Требуемые соотношения выполняются.

Вычислим вероятности состояний в переходном режиме, полагая l = 5, m = 10. Промежуточные результаты расчета приведены в табл. 1.1.

Произведя вычисления с точностью до одной сотой, получим

Т а б л и ц a 1.1

k	Sk		D0(Sk)	D1(Sk)	D2(Sk)
	-7, 93	14, 14	-35	10, 4
	-22, 07	-14, 14		-60, 4

Для наглядности полученные зависимости изображены на рис. 1, откуда видно, что, начиная примерно с t = 0, 8, в системе устанавливается стационарный режим.

Pk(t)

Рис. 1.

При оценке этих результатов следует иметь в виду, что время измеряется в условных единицах, точнее – в тех же единицах, которые были использованы при задании интенсивностей l и m. Так, например, если l = 5 следует понимать как 5 требований в минуту, то стационарный режим в системе наступает примерно через 50 с после начала функционирования, если же l = 5 означает 5 требований в сутки, то стационарный режим возникает спустя 19, 2 ч.

Имея распределение вероятностей, можно для фиксированного значения t находить числовые характеристики эффективности функционирования системы. Так, например, при t = 0, 1 вероятность того, что канал занят, равна p(0, 1) = 0, 22, вероятность отказа P_отк(0, I) = 0, 05, среднее число занятых каналов a(0, 1) = I, p(0, 1) = 0, 22.

Исследование численным методом. Как уже отмечалось, как правило, в силу высокого порядка системы дифференциальных уравнений (1.1) анализ нестационарного режима работы СМО аналитическим методом чрезвычайно затруднен. В этих случаях используют численный метод интегрирования системы (1.1) на ЭВМ с помощью известных методов Рунге - Кутты, Эйлера и т.д. Инструкцию по работе с программой для исследования нестационарного режима марковских СМО получить у преподавателя.

Контрольные вопросы.

1. Какие случайные процессы называются марковскими? Какова специфика математического описания этих процессов?

2. Почему процесс обслуживания в СМО типа M/M/n является марковским?

3. К какому типу принадлежат дифференциальные уравнения для вероятностей P_k(t)?

4. Поясните применительно к рассматриваемой системе условия существования стационарного режима (режима статистического равновесия).

5. В чем состоят затруднения при исследовании нестационарного режима?

6. Какие возникают трудности при аналитическом исследовании нестационарного режима с помощью преобразований Лапласа?

7. В чем заключается основное ограничение в применении этого метода? Перечислите известные Вам численные методы решения систем дифференциальных уравнений.

8. В чем состоит метод Рунге - Кутты? Опишите вычислительную процедуру метода.

9. Как влияют на длительность нестационарного режима параметры СМО? Для ответа на этот вопрос необходимо ознакомиться с результатами расчета всех вариантов задания.

Работа № 2. ИССЛЕДОВАНИЕ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ МЕТОДОМ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ.

Цель работы – изучение возможностей применения метода имитационного моделирования для исследования СМО.

Порядок выполнения работы.

1. Ознакомиться с методическими указаниями.
2. Для заданного варианта СМО подготовить программу и составить план проведения машинных экспериментов в соответствии с заданием.
3. Провести эксперимент на ЭВМ.
4. Обработать результаты машинных экспериментов – построить графики зависимостей характеристик СМО от варьируемых параметров.
5. Оформить отчет, в котором привести описание исследуемой СМО, результаты машинного счета, основные соотношения и результаты вычислений, графики, выводы на основе полученных результатов.
6. Ответить на контрольные вопросы.

Основные положения.

Применение аналитических и численных методов исследования СМО ограничено случаями, когда система является марковской и описывается уравнениями размножения и гибели или может быть сведена к ней. В противном случае исследование СМО возможно с помощью метода имитационного моделирования, основанного на многократной имитации с помощью ЭВМ процессов, протекающих в системе, с последующей статистической обработкой полученных результатов.

В качестве основных величин, характеризующих функционирование исследуемой СМО используют оценки математического ожидания числа занятых каналов, длины очереди, времени ожидания заявок в очере­ди, вероятностей обслуживания заявок, и др. Так, для момента времени t (o£ t£ T_н), где T_н - время моделирования, могут быть вычислены

- оценка математического ожидания числа занятых каналов:

здесь - число занятых каналов в момент времени t в j-й реализации; N – число реализаций (прогонов модели);

- оценка вероятности того, что в системе в момент времени t есть k требований:

здесь - число реализаций, в которых на момент времени t в системе было k требований;

- оценка вероятности, что требование получит отказ:

где - общее число требований, появившихся к моменту времени t в j-й реализации; - число требований, получивших отказ к моменту времени t;

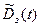- оценка дисперсии числа занятых каналов в момент времени t:

Для получения представления о точности и надежности этих оценок могут быть найдены доверительные интервалы I_b при заданной доверительной вероятности b.

1. Для математического ожидания числа занятых каналов

Значение t_b берется из распределения Стьюдента при (N-1) степенях свободы. При больших N (N> 30) вместо распределения Стьюдента можно пользоваться нормальным законом. В этом случае

где Ф(х) - интеграл вероятностей:

2. Для вероятностей

Здесь

При больших N приближенно

,

где - С.К.О. оценки вероятности :

Кроме того, границы доверительных интервалов для вероятностей могут легко быть найдены из номограмм.

Пример СМО. Рассматривается n-канальная СМО с ограниченным временем ожидания в очереди t. Количество мест в очереди ограничено числом m. На вход системы поступает стационарный поток требований. Функция распределения F(t_инт) интервалов времени между соседними требованиями задана. При наличии свободного канала обслуживания требование начинает обслуживаться. Длительность обслуживания t_обс - величина случайная и подчинена закону распределения G(t_обс). Если при поступлении требования все каналы заняты, то оно помещается в очередь, откуда поступает на обслуживание при освобождении одного из каналов. Если время ожидания требования в очереди t_ож достигает величины t, то оно покидает систему необслуженным. Допустимое время t ожидания требования в очереди случайно, его закон распределения H(t). Если при появлении требования очередь полностью заполнена, то требование покидает систему необслуженным.

Для заданной СМО требуется:

1. Исследовать возможность применения метода имитационного моделирования для анализа СМО. С этой целью принять законы распределения F(t_инт) и G(t_обс) экспоненциальными. Величину t принять неслучайной, t> Т_мод. Найти точечные и интервальные оценки для P_k(t), k=0, n+m, a(t), средней длины очереди, P_отк(t). Сравнить полученные результаты с результатами численного интегрирования из работы № 1.

2. Исследовать влияние величины допустимого времени Т ожидания требования в очереди на характеристики системы: а) при экспоненциальном законе распределения Н(t) и б) при t=const (F(t) и G(t) – экспоненциальные).

3. Исследовать влияние на характеристики системы законов распределения F(t) и G(t), варьируя для заданного вида закона рас­пределения значениями его параметров. Результаты моделирования сравнить с результатами численного интегрирования.

Порядок проведения имитационных экспериментов.

Для проведения имитационных экспериментов используется стандартная программа, реализующая двухканальную СМО. Для генерации случайных величин с заданными законами распределения F(t) и G(t) в них применяются подпрограммы, использующие датчик псевдослучайных чисел, равномерно распределенных в интервале [0, 1].

Инструкцию по работе с программой и варианты заданий получить у преподавателя.

Контрольные вопросы.

1. Когда целесообразно для исследования СМО применять метод имитационного моделирования?

2. В каких случаях СМО не может быть описана с помощью уравнений размножения и гибели?

3. Как вычисляются точечные и интервальные оценки параметров СМО по результатам моделирования?

4. Как влияют вид и параметры законов распределения на характеристики СМО?

Работа №3. ИССЛЕДОВАНИЕ НАДЕЖНОСТИ РЕЗЕРВИРОВАННОЙ

ВОССТАНАВЛИВАЕМОЙ СИСТЕМЫ МЕТОДАМИ ТЕОРИИ

МАССОВОГО ОБСЛУЖИВАНИЯ

Цель работы - приобрести практические навыки использования методов теории массового обслуживания для исследования надежности систем, изучить влияние отдельных параметров системы на ее надежность.