Свойства равномерно сходящихся рядов.

1. Теорема о непрерывности суммы равномерно сходящегося ряда непрерывных функций. Если члены функционального ряда - непрерывные функции, и этот ряд равномерно сходится на отрезке , то сумма этого ряда непрерывна на .

2. Теорема о почленном интегрировании равномерно сходящегося ряда. Пусть члены функционального ряда непрерывны на отрезке , и ряд равномерно сходится к своей сумме на этом отрезке: . Тогда , т.е. интеграл от суммы ряда равен сумме ряда, составленного из интегралов от членов равномерно сходящегося ряда.

3. Теорема о почленном дифференцировании равномерно сходящегося ряда. Пусть члены сходящегося ряда - дифференцируемые на отрезке функции, и ряд, составленный из производных , равномерно сходится на . Тогда ряд можно почленно дифференцировать, и , т.е. производная суммы ряда равна сумме ряда из производных.

4) x^2+z^2=4, Y=5, Y=x

5) Вычислить криволинейный интеграл по ф-ле грина

Решение:

= -1/2

6)

Т. к. 1/n ~ гармоническому ряду, ограничен, монотонный, а сходится по признаку сравнения с рядом Дирихле, то сходится абсолютно по Абелю.

б)

Д:

Билет 24.

1). Теорема о за мена переменных в тройном интеграле. Пусть в пространстве Ouvw задана область G, и пусть отображение преобразует эту область в область V пространства Oxyz. Будем считать, что отображение F задаётся функциями . Пусть: 1). F взаимно однозначно отображает G на V; 2). Функции x ( u, v, w ), y ( u, v, w ), z(u, v, w) непрерывно дифференцируемы на G (имеют непрерывные частные производные); 3). Якобиан не обращается в нуль на G. Тогда .

В цилиндрических координатах .

В сферических к-тах

2) Векторное поле называется центрально-симметричным, если оно центрально, и функция u (M) зависит только от расстояния r, т.е. от длины радиуса-вектора точки М: (). Так как , , то для центрально-симметричного поля , .

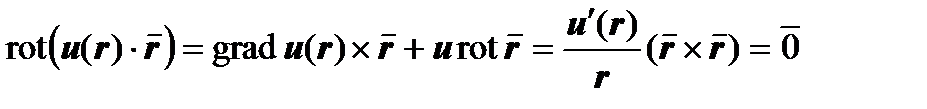вид центрально-симметричного поля, для которого дивергенция равна нулю (в дальнейшем мы будем называть такие поля соленоидальными): .

Таким образом, соленоидальны только те центрально-симметричные поля, в которых зависимость от r такая же, как в законах Кулона и всемирного тяготения. В связи с этим встают мировоззренческие вопросы о том, вычислял ли Господь Бог дивергенцию, когда создавал Вселенную, и о связи показателя степени в знаменателях законов Кулона и всемирного тяготения с пространственной размерностью мира, в котором мы живём

3). Теорема Абеля. Если степенной ряд сходится в точке 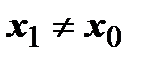, то

1. он абсолютно сходится в любой точке х, удовлетворяющей неравенству (т.е. находящейся ближе к точке 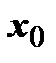, чем );

2. он сходится равномерно на любом отрезке , целиком лежащем на интервале (т.е. на интервале с центром в 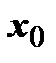радиуса ).

3. Если этот ряд расходится в точке , то он расходится в любой точке х, удовлетворяющей неравенству (т.е. находящейся дальше от точки 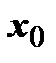, чем ).

4. Доказательство. 1. Из сходимости ряда в точке следует, что его общий член стремится к нулю при ; любая последовательность, имеющая предел, ограничена, следовательно, существует число С такое, что . Пусть точка х удовлетворяет неравенству , тогда . Оценим член ряда в точке х:

5. . Члены ряда в точке х по абсолютной величине не превосходят членов сходящейся геометрической прогрессии, следовательно, ряд сходится абсолютно в точке х, следовательно, он сходится абсолютно в любой точке интервала .

6. 2. Пусть отрезок , целиком лежит на интервале . Из точек а, b выберем ту, которая находится дальше от точки 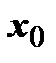, примем для определённости, что это - точка а: . Тогда для любого х из этого отрезка 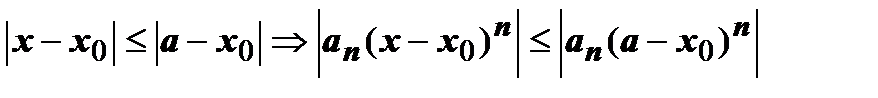. В точке ряд , по доказанному, сходится абсолютно, но он является на мажорантой для ряда , следовательно, степенной ряд сходится равномерно на отрезке .

7. 3. Пусть степенной ряд расходится в точке , и . То, что ряд расходится в точке х, докажем от противного. Если предположить, что он сходится в точке х, то, по доказанному, он сходится во всех точках, расположенных ближе к 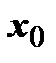, чем х, следовательно, он сходится в точке , что противоречит условию.

4) Вычислить объем тела ограниченного поверхностями z=0, z=4-y, x= , x=2

8. V= =

9. 5)вычислить массу пов-ти z= , плотности

10. M=

11. =

12. M= dxdy=6 =54pi

13. 6) а)

14. Т к ~ 1/n, то ряд расходится абсолютно,
и т.к ряд сходится по лейбницу, то ряд сходится условно.

15. б)

16. Д: =