
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Бесконечно малые и бесконечно большие функции
|
|
Функция  называется бесконечно малой при
называется бесконечно малой при  если
если  .
.
Функция  называется бесконечно большой при
называется бесконечно большой при  если для любого, сколь угодно большого
если для любого, сколь угодно большого  , найдется такое положительное число
, найдется такое положительное число  что при всех
что при всех 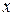 , удовлетворяющих условию
, удовлетворяющих условию 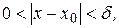 выполняется неравенство:
выполняется неравенство:  .
.
Запись:  .
.
Если  – бесконечно малая функция при
– бесконечно малая функция при  то
то  – бесконечно большая функция при
– бесконечно большая функция при  .
.
Бесконечно малые функции  и
и 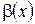 называются эквивалентными, если
называются эквивалентными, если
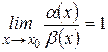 (
( при
при 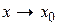 ).
).
В частности, являются эквивалентными функции  при
при 
Если 
 при
при  и существует
и существует  то
то

Если  то функция
то функция  называется бесконечно малой более высокого порядка по сравнению с
называется бесконечно малой более высокого порядка по сравнению с  .
.
Обозначение:
 .
.
Если  ,
,  , то
, то  называется бесконечно малой одинакового порядка малости по сравнению с
называется бесконечно малой одинакового порядка малости по сравнению с  или говорят, что
или говорят, что  является бесконечно малой –
является бесконечно малой –  - го порядка малости по сравнению с
- го порядка малости по сравнению с 
Обозначение:
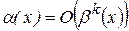
Если 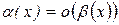 , то
, то
 .
.
|
|