Дискретное вейвлет преобразование одномерного сигнала

Цифровая обработка сигнала требует его дискретизации. Как и в случае преобразования Фурье существует дискретная форма вейвлет преобразования. Выше было отмечена определенная степень свободы в выборе базиса вейвлет преобразования. В данном разделе нами будет использоваться один из самых простых вейлвет базисов – базис Хаара.

Рассмотрим дискретизированный и квантованный сигнал (сигнал 2.1) – рисунок 2.1 (а). Будем постепенно усреднять данный сигнал, усредняя попарно его отсчеты. Таким образом, каждый шаг усреднения будет сокращать разрешение сигнала в 2 раза (т.е. для его представления будет требоваться в два раза меньшее число отсчетов). Однако при таком усреднении мы теряем часть информации о сигнале, для того чтобы восстановить сигнал после усреднения нам потребуется дополнительная информация. Будем сохранять разности между усредненным отсчетом и отсчетами, из которых усредненный отсчет состоит при более высоком разрешении. Данные разности показывают детали сигнала – его флуктуации вокруг среднего при данном уровне разрешения. На рисунке 2.1 детализирующее коэффициенты показаны в правой части рисунков 2.1 (б, в, г, д). Теперь воспользовавшись детализирующими коэффициентами мы сможем восстановить прежнею форму сигнала.

Таким образом, для того чтобы перейти от одного, более низкого уровня разрешения к более детализированному уровню нам требуется знать усредненные отсчеты сигнала и детализирующие коэффициенты.

Заметим, что сигнал 2.1, изображенный на рисунке 2.1 (а), может быть представлен следующим образом – , где - некоторые базисные функции, а – координаты сигнала 2.1 в этом базисе. Очевидно, что если мы выберем в качестве единичную ступеньку, изображенную на рисунке 2.2 (а), то, сдвигая необходимое число раз, мы сможем представить сигнал 2.1 с помощью суммы таких единичных ступенек. Таким образом, мы ввели базис, в котором мы можем представить сигнал 2.1. Отметим, что поскольку функции , изображенные на рисунке 2.2, не пересекаются между собой, то построенный нами базис является ортогональным. Функции называются масштабирующими функциями.

Рисунок 2.1 – Усреднение дискретизированного сигнала 2.1

Рисунок 2.2

Теперь необходимо ввести некоторый базис для представления детализирующих коэффициентов. Такой базис был введен Хааром и его базисные функции, названные вейвлетами, изображены на рисунке 2.2 (б).

Рассмотрим теперь процедуру усреднения сигнала, проиллюстрированную на рисунке 2.1, с точки зрения только что введенных базисов. Рассмотрим конкретный сигнал, заданный следующим вектором значений – [9 7 3 5]. С помощью масштабирующей функции Хаара мы можем представить сигнал так, как это изображено на рисунке 2.3.

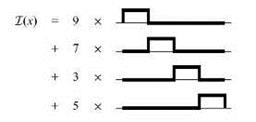
Рисунок 2.3 – Представление исходного сигнала в базисе Хаара

Проведем процедуру декомпозиции сигнала на две части – усредненный сигнал с двое уменьшенным разрешением и детализирующие коэффициенты. Получим следующий вектор – = [8 4 | 1 –1], представление которого в базисе Хаара с помощью масштабирующей функции и вейвлетов изображено на рисунке 2.4.

Рисунок 2.4 – Представление усредненного сигнала в базисе Хаара

Выделим в векторе [8 4 | 1 –1] часть, представляющую усредненный сигнал (первая половина вектора), и проведем относительно неё повторное усреднение и нахождение детализирующих коэффициентов. Получим следующий вектор – [6 | 2 1 –1] представление которого в базисе Хаара с помощью масштабирующей функции и вейвлетов изображено на рисунке 2.5.

Рисунок 2.5 – Представление дважды усредненного сигнала в базисе Хаара

Таким образом, мы представили исходный сигнал с помощью его усредненной части (среднего по сигналу) и детализирующих коэффициентов. Отметим, что размерность исходного и преобразованного векторов совпадают, это говорит о том, что при преобразовании не было потерь информации и, следовательно, возможно полное восстановление исходного вектора. Шаги описанной процедуры ещё раз проиллюстрированы на рисунке 2.6.

Рисунок 2.6 – Представление сигнала в базисе Хаара

Отметим, что если мы будем восстанавливать сигнал после его разложения в базисе Хаара, то мы можем остановить процесс восстановления «на полпути» и получить представление сигнала с заданным разрешением. Другими словами нами получен математический инструмент изменения разрешения сигнала.