
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Понятие производной функции в точке
|
|
Содержание учебного материала.
1. Приращение аргумента и приращение функции.
2. Введение понятия производной (задача о скорости).
3. Алгоритм вычисления производной.
4. Табличные производные.
5. Контрпример.
6. Геометрический смысл производной.
7. Уравнение касательной.
2. Введение понятия производной.
Задача. Материальная точка движется по закону  где S –путь в метрах, t – время в секундах. Найдите
где S –путь в метрах, t – время в секундах. Найдите
1) среднюю скорость, если  ; мгновенную скорость, если t = 3;
; мгновенную скорость, если t = 3;
2) среднюю скорость, если  , мгновенную скорость, если t = t0.
, мгновенную скорость, если t = t0.
Решение

1)  (м/с).
(м/с).

 .
.


2)


По аналогии введём понятие средней и мгновенной скорости изменения функции. Пусть дана функция  , определённая в окрестности точки
, определённая в окрестности точки  и Dх – приращение
и Dх – приращение  такое, что
такое, что  принадлежит области определения функции f. Тогда средняя скорость изменения функции равна отношению приращения функции к приращению аргумента, а мгновенная скорость – пределу этого отношения при D х стремящемся к 0.
принадлежит области определения функции f. Тогда средняя скорость изменения функции равна отношению приращения функции к приращению аргумента, а мгновенная скорость – пределу этого отношения при D х стремящемся к 0.


Если предел существует, то мгновенная скорость - это скорость изменения функции в точке  . По другому она называется производной функции f в точке
. По другому она называется производной функции f в точке  . Обозначение:
. Обозначение: 
Таким образом,  =
= 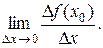
Алгоритм нахождения производной функции f в точке х 0.
1. Придаём приращение аргументу: 
2. Находим приращение функции6 
3. Находим отношение приращений:  =
= 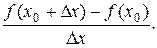
4. Находим предел отношения приращений: 
По определению выводим производные функций 
Составляем таблицу.
| f (x) | c | kx+b | xn, nÎ N, n¹ 1 | 
| 1/ x |
| f¢ (x) | k | nxn-1 | 1/2 
| -1/ x2 |
В дальнейшем таблица будет дополнена производными тригонометрических, показательной и логарифмических функций.
Кроме табличных производных, учащиеся пользуются правилами нахождения производной суммы, произведения, дроби, а также производной сложной функции.
Целесообразно рассмотреть пример функции  , которая в точке 0 не имеет производной, так как не существует
, которая в точке 0 не имеет производной, так как не существует 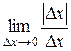 (рис.9)
(рис.9)
Следует также обратить внимание учащихся на то, что график в этой точке терпит «излом» (рис. 10).


При выводе правила вычисления производной произведения устанавливается взаимосвязь между непрерывностью и дифференцируемостью функции в точке. Приводится лемма: если функция f дифференцируема в точке х 0, то она непрерывна в этой точке. Обратная теорема неверна. Показать, что обратная теорема неверна можно посредством приведённого примера: функция у =  непрерывна, но не дифференцируема в точке 0.
непрерывна, но не дифференцируема в точке 0.
Реализуя алгоритм нахождения производной на графике функции, учащиеся приходят к выводу, что значение производной в точке с абсциссой х 0 равно угловому коэффициенту касательной к графику функции, проведённой через эту точку.

tgj = 
|
|