Понятие предела функции в точке

Начала анализа в 10 – 11 классах средней школы

Понятие предела функции в точке вводится в курсе математики старших классов в связи с необходимостью определения производной. История изучения пределов в школе достаточно многообразна. Были попытки строгого определения этого понятия на языке e-d. Однако практика обучения отвергла такие попытки.

Рассмотрим один из возможных вариантов формирования понятия предела функции в точке на интуитивно-наглядном уровне.

Учащимся предлагается задание 1. Рассмотрим функцию . Пусть переменная х принимает значения «приближающиеся» к 1 сначала справа, а затем слева. Понаблюдаем за соответствующими значениями у по графику.

Работаем по подготовленному заранее графику.

Приходим к выводу, что при х ® 1 значения у® 3.

Вывешиваем плакат.

К такому выводу можно прийти аналитически.

Будем приближаться к 1 справа с помощью последовательности значений аргумента . Вычисляем несколько первых членов этой последовательности:

Найдём соответствующую последовательность значений функции

Аналогично будем приближаться к 1 слева с помощью последовательности значений аргумента . Тогда соответствующая последовательность значений функции также приближается к 3.

Делаем вывод: если аргумент принимает бесконечную последовательность значений, стремящуюся к 1, то соответствующая последовательность значений функции стремится приблизиться к 3.

В такой ситуации говорят, что при х ® 1 у ® 3 и записывают так .

Затем аналогичные наблюдения и рассуждения проводятся по готовому чертежу на плакате 2 для функции

Предлагаем учащимся последовательность значений и . Делаем вывод, что если х ® -3, то у ® - 6. Записываем .

Далее рассматривается функция 3

Наблюдаем за поведением функции при По графику делаем вывод, что . То есть .

Далее обобщаем полученные результаты.

1. Каждая из рассмотренных функций определена в некоторой «проколотой» окрестности точки а.

2. Существует число А, к которому стремятся значения функции, если значения аргумента стремятся к числу а.

График функции в случае существования предела имеет один из трёх видов:

Точка на графике Точка «выколота» Точка «выскочила»

Далее со школьниками целесообразно обсудить контрпримеры.

Работая с графиками, учащиеся должны ответить на вопрос: «Имеет ли данная функция предел в точке 0?»

Для усвоения понятия предела на интуитивно – наглядном уровне школьникам могут быть предложены упражнения (Рис. 1 – Рис. 6).

Существует ли предел в точке 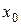и, если существует, то чему он равен?

В дальнейшем для нахождения табличных производных учащиеся должны знать теоремы о пределах, которые сообщаются им без доказательства.

Теорема 1.

Пусть , тогда

Теорема 2.

Если функции f и g имеют пределы в точке а, то

Теорема 2.

Если функции f и g имеют пределы в точке а, то

Cледствие.

Теорема 3.

Если функции f и g имеют пределы в точке а, причём , то

.

Разъяснить смысл теорем 1 и 2 можно с помощью графиков. На примере функции покажем, что

Приведём пример задания, иллюстрирующего применение теорем о пределах.

Дано:

Найти: