Случайный и типический отбор.

Случайный отбор:

- простой случайный способ – объекты выбираются из выборки случайным, наугад образом.

- случайный способ с использованием таблиц случайных чисел – отбор ведется по номерам, взятым из таблиц случайных чисел.

- механический отбор – в выборку берут каждый 5...7 объект, однако надо следить за тем, чтобы синхронно с номерами не повторялось какое-либо внешнее условие, влияющее на свойства объекта.

- другой вариант механического отбора – генеральная совокупность делится на несколько частей, затем из каждой группы случайным образом выбирается 1 или несколько единиц наблюдения.

Типический отбор – используется в случаях, когда случайная выборка с биологической точки зрения не соответствует условиям сбора материала или самой задачи исследования. Первое может произойти, когда исследователь вынужден довольствоваться малым объемом выборки (20 ед. и меньше). Второй случай, когда объекты наблюдения размещены в пространстве неравномерно, поэтому исследователь должен выбрать наиболее типичное с точки зрения биологии состояние (место) объекта и произвести выборку случайным образом.

При использовании случайного отбора хорошо характеризуется изменчивость признака и неточно отображать средние значения. При типической выборке довольно точно рассчитывается среднее значение и искажается характер изменчивости (при условии, что выборка небольшая).

Смешанный отбор – используется не смотря на неравномерное размещение объектов требующих получить представление о совокупности популяции в целом. Территории делят на участки (группы) соответствующей градации ее неоднородности, затем из каждой группы случайным способом отбирают одинаковое, а чаще пропорциональное число едниц.

19. Группировка данных: основные понятия, техника проведения в зависимости от вида вариации

20. Среднее арифметическое, взвешенное, квадратичное, кубическое и гармоническое, назначение средней

ü Среднее арифметическое – простое для не сгруппированной выборочной совокупности:

Взвешенное

– ср. значение класса

- частота соответствующего класса

N – объем выборки

Значение ср. арифметического отражается всей совокупностью в целом, дает свободную обобщенную характеристику изучения признака. При определении ср. арифметического взаимно поглощаются отметаются случайные колебания, отклонения от центральной тенденции от уровня вариационного ряда. Где выступает общий закон явлений вскрывается типичная для всей совокупности в целом.

ü Среднее квадратическое. Используется как более точное значение при работе с площадными характеристиками.

для не сгруппированной выборки

для сгруппированной выборки

ü Среднее кубическое – используется как более точное среднее при работе с объемными характеристиками.

не структурная

структурированная

ü Средняя гармоническая – используется тогда когда результаты наблюдений заданы вариантом.

для сгруппированной

21. Свойства средней арифметической

a) Если к каждой варианте прибавить или отнять одну и ту же величину, то ср. арифметическое соответственно уменьшится или увеличится на столько же

b) Если каждую варианту разделить или умножить на одно и то же число то ср. значение измениться во только же раз

c) Алгебраическая сумма отклонения вариант от ср. арифметического равна 0

d) Сумма квадратов отклонений варианта от ср. арифметического меньше суммы квадратов отклонений варианты от любой другой величины не раной ср. арифметическому

22. Мода и медиана

Структурные средние – мода и медиана

Мода – наиболее часто встречающееся значение случайной величины

Медиана - это варианта, делящая (в порядке возрастания) вариационный ряд пополам

23. Меры изменчивости. Свойства дисперсии

Среднее арифметическое показывает какое значение признака наиболее характерно для данной совокупности, но сама по себе она еще недостаточно для характерной совокупности, т.к. главной особенностью совокупности является разнообразие между ее членами, т.е. изменчивостью (вариацией).

Поэтому для характеристики совокупности используют показатели вариации:

- лимиты (крайние значения выборки max и min)

- размах вариаций (разность между max и min вариантой)

Данные показатели хотя и просты в определении, но мало эффективны для анализа.

Можно было бы использовать среднее значение отклонения вариант от среднего, но как известно из 3 свойства: сумма отклонения = 0. поэтому используют такие показатели как дисперсия и среднеквадратическое отклонение.

D=сигма в квадрате=сумма (Xi-X)в квадрате/N-1 для не сгруппированной выборки

D=сумма(Xi-X с чертой)в квадрате ni/N-1 для сгруппированной выборки, n меньше 100

D=сумма(Xi-X с чертой)в квадрате ni/N для сгруппированной выборки, n больше 100.

Дисперсия является мерой рассеяния случайной величины.

Свойства дисперсии:

1. если каждую варианту увеличить или уменьшить на одно и то же число, то дисперсия не изменится.

2. если каждую варианту выборки умножить или разделить на одно и то же постоянное число a, то дисперсия увеличится или уменьшится в а² раз.

Однако как самостоятельная статистика дисперсия для анализа, как правило, не используются, а служат промежуточным звеном в вычислениях.

кореньD=сигма – среднеквадратическое отклонение или стандартное отклонение.

Оно показывает на сколько в среднем отличается значение варианты от среднего значения, таким образом стандартное отклонение является натуральным показателем изменчивости (при равноточных измерениях характеризует случайную ошибку измерения) однако такой показатель неудобен и редко используется для анализа и служит промежуточным звеном в вычислениях.

V= сигма/Xс чертой*100% - коэффициент вариации

Данный показатель является относительной величиной и удобен для анализа. Показывает на сколько % в среднем может отличаться значение случайной величины от среднего.

До 10% слабое варьирование

11-25% среднее

Более 25% значительное

Нормированное отклонение – это отклонение той или иной варианты от среднего арифметического отнесенное к среднеквадратическому отклонению.

t=Xi-X с чертой/сигма

этот показатель позволяет измерять отклонение отдельных вариант от среднего уровня и сравнивать их для разных признаков, т.е. можно сравнивать места, занимаемые особью, по каждой из этих признаков в их распределении.

24. Понятие нормального распределения

Если мы изучаем какой-либо признак в выборке, то различные значения

изучаемого признака встречаются неодинаковое число раз: одни чаще, другие реже.

Это явление называется распределением признака. Изобразить распределение признака

можно с помощью вариационного ряда, вариационной кривой, гистограммой,

кумулятой. В большинстве распределений проявляется определенная закономерность:

крайние значения (наименьшие и наибольшие) появляются редко; чем ближе значение

признака к средней арифметической, тем оно чаще встречается; в центре распределения

имеются такие значения, которые встречаются наиболее часто и образуют в

вариационном ряду модальный класс. Подобное распределение значений часто

встречается, что первоначально принималось за норму всякого массового случайного

события и поэтому получило название нормального распределения.

Рис 4. Кривая нормального распределения

25. Ошибка репрезентативности для среднего арифметического, среднеквадратического отклонения, коэффициента вариации. Доверительный интервал, оценка достоверности статистики

С помощью статистик, выбранные совокупности пытаются описать статистики генеральной совокупности.

Статистики выборки отличаются от статистик генеральной совокупности.

Разница между этими статистиками называют ошибкой репрезентативности, и чем больше объем выборки, тем меньше эта ошибка.

mx с чертой = сигма/кореньN ошибка среднего значения

mc = сигма/корень2N ошибка стандартного отклонения

mа = корень (сигма /N) ошибка коэф. ассиметрии

mэ = 2mа ошибка коэф. экцесса

С помощью ошибки можно определить является ли статистика выборочной совокупности закономерной или случайной величиной.

Можно проверить достоверность статистики, для этого используют t критерий Стьюдента.

Он относится к параметрическим критериям. Это статистический критерий, с помощью которого можно установить достоверность различия между параметрами вариационных рядов одноименного признака в 2х выборках.

t расчетное = S t / m st

t расчетное нужно сравнивать с t табличным

df = n-1

уровень значимости α выбирается самим исследователем и зависит от уровня ответственности вывода (чем меньше α, тем строже вывод).

Если t расчетное больше t табличного, то статистика достоверна при заданном уровне значимости.

t выч = модуль X1-X2 / корень(m x1)в квадрате + (m x2)в квадрате

dt=n 1+n 2 – 2

t выч = модуль V1-V2 / корень (m v1)в квадрате + (m v2)в квадрате. Для коэф. вариации.

dt=n 1+n 2 – 2 достоверно когда t выч меньше t табл

сравнение между собой стандартных отклонений:

t выч = модуль сигма1-сигма2 / корень (сигма /2*n 1)в квадрате + (сигма /2*n 2)в квадрате

dt=n 1+n 2 – 2 достоверно когда t выч больше t табл

26. Точность опыта. Определение необходимого объёма выборки

27. Коэффициенты асимметрии и экцесса: назначение, графическая интерпретация, ошибка. Предварительная оценка согласованности эмпирического ряда распределения с нормальным распределением

Коэф. ассиметрии – показатель крутости ряда распределения относительно нормальной кривой.

Коэф. > 0 – левосторонняя ассиметрия. Максимум эмпирической кривой смещён влево относительно нормального распределения

Коэф. = 0 кривая симметрична

Коэф. < 0 правый склон круче правого. Максимум смещён вправо

Коэф. экцесса – показатель косости ряда распределенияю

Коэф. > 0 – положительный экцесс. Имеет место островершинное распределение.

Коэф. = 0 – эмп. распределение по косости сходно с нормальным распределением

Коэф. < 0 – отрицательный экцесс. Плосковерхое распределение

Коэф. экцесса не может быть больше 3

Если коэф экцесса больше или равен 2, то имеет место бимодальное (двугорбое распределение), то есть иемеют место 2 разнородные стат. совокупности.

Если коэф. ассиметрии положительный, то основная часть объекта в левой части распред.

Если коэф экцесса положительный, то объект расположен в центральных классах, если отрицательный, то объект распылен.

28. Статистические критерии. Основные понятия. Виды статистических критериев

«Нулевая» гипотеза- говорит о случайности имеющих место явлений.

«Альтернативная» гипотеза – имеющее место явление в какой то степени закономерно.

Критерий достоверности – это величины распределений, которые известны. Позволяют в каждом конкретном пункте определить, удовлетворяют ли выборочные показатели принятые гипотезы.

Функции распределения указывают величину приводящую в спец. Таблицах для каждой из степеней свободы и формы значимости.

Степень свободы – число свободы варьирующих ед. в составе численно ограниченной стат. совокупности.

Если совокупность состоит из n- го числа членов и проявляется средней величиной.

Хор. То что любой член совокупности может иметь какое угодно значение не изменяя среднюю, кроме одной. варианты, значение которой определяют разностью между суммой значимости всех основных вариантов и величиной N. Хор. Следовательно, одного варианта численно ограниченного стат. Совокупностью не имеет свободы вариации. Т.о число степеней свободы К = dF =n – 1.

Уровень значимости – вероятностей ошибки, допускаемой при оценке какой либо гипотезы, проще говоря вероятность справедливости альтернативной гипотезы.

29. Критерий Стьюдента: вид, назначение, расчёт, анализ, пример

Для проверки достоверности статитистики используют t критерий Стьюдента.

Он относится к параметрическим критериям. Это стат. критерий, с помощью которого можно установить достоверность различия между параметрами вариационных рядов одноименного признака в 2-ух выборках.

t расчётн = St/Mst

полученное значение надо сравнить с табличным

Уровень значимости выбирается самим исследователем и зависит от уровня ответственности вывода

Если расчётное больше табличного, то статистика достоверна

Пример. X с черточкой сверху = 20, Mx с чёрточкой = 2, N = 100, уровень = 1%

Tp = 20/2 = 10, df = 99, Tst = 2, 58

Статистика достоверна, т.к. tрасчёт больше tтаблич

30. Критерий Фишера: вид, назначение, расчёт, анализ, пример

31. Критерий хи-квадрат: вид, назначение, ограничения по применению, расчёт, анализ, пример

Непараметрические критерии – это статистические критерии, с помощью которых устанавливается степень сходства и различия эмпирического и теоретического или двух эмпирических рядов распределения признака, в целом и который требует для своего знания ряда.

Применение .

Применяется для установления:

a) Степени соответствия эмпирических наблюдений и теоретических ожидаемых данных.

b) Для определения степени соответствия сходства двух эмпирических рядов.

Ограничения

1. Объемы выборок должны быть не менее 50

2. Частота классов не должна быть менее 5 т.к. на концах рядов это случается часто, то соответствующие классы необходимо объединять.

3. Критерий применим только к абсолютному значению

определяют по приложению 2 при разных уровнях значимости.

нормальный закон

Если вычисленное меньше табличного то эмпирическое распределение подчиняется теоретическому закону (согласуется с теоретическим распределением). Если наоборот, значит что распределение не подчиняется.

Нулевая гипотеза. Говорит, что различий между теоретическим и эмпирическим распределением нет => уровень значимости – это степень вероятности, правильности истинности нулевой гипотезы.

100 если то нулевая гипотеза верна

32. Критерий Колмогорова-Смиронова: вид, назначение, расчёт, анализ, пример

Применяется для установления степени соответствия эмпирических наблюдаемых и теоретических ожидаемых данных, для установления степени соответствия 2-х эмпирических вариационных рядов

Основан на сравнении частот 2-х распределений, не требует объединения частот (когда они (их) не меньше 5)

Частоты могут быть относительными и абсолютными. Нет жёстких ограничений по объёму выборки.

Применение данного критерия предпочтительней в случае дискретного варьирования.

Имеет три пороговых значения.

Если лямбда вычисленная > лямбда стандартная, то распределение не согласуется

Лямбда = Dmaх / корень из n

Где Dmaх – максимальная разница между накопленными частотами

N – объём выборки

Лямбда = Dmaх * корень n1*n2/n1+n2 – для разных объёмов выборки

N1 – объём первой выборки

N2 – второй

Пример. Число утят в 2-х выводках

Суммы: 63 и 66, 0, 024 – Dmaх

Лямбда = 0, 024 * корень63*66/63+66 = 0, 136

Уровень значимости = 0, 05%

согласуется

33. Моделирование распределения

Цель: 1. выравнивание эмпирических частот 2. Сравнение двух распределений 3. Прогнозирование, предсказание.

Зная закон распределения можно предсказать, с какой вероятностью будет принимать признак то или иное значение.

Теоретические законы

1. Нормальное распределение

2. Распределение Вейбула и др.

У каждого распределения есть свои параметры

нормальный закон

Порядок моделирования распределений

1. Рассчитывают и исследуют значения коэффициента асимметрии и экцесса, определяют достоверность, если оба коэффициента не достоверны, то распределение, может быть подчиняется нормальному закону. Если хотя бы один коэффициент достоверен, то эмпирическое распределение подчиняется нормальному закону.

2. Если есть подозрения, что подчиняется закону, что починяется закону, то рассчитывают частоты териотечески нормального распределения. И с помощью определяют принадлежность к нормальному закону.

Во втором случае сразу пытаются подобрать иное распределение.

34. Дисперсионный анализ: назначение, использование в лесном деле, условия для правильного применения, теоретическая схема, анализ по результатам расчётов

Дисперсионный анализ (от латинского Dispersio – рассеивание) применяется для исследования влияния одной или нескольких качественных переменных (факторов) на одну зависимую количественную переменную

Основной целью дисперсионного анализа является исследование значимости различия между средними с помощью сравнения (анализа) дисперсий. Разделение общей дисперсии на несколько источников, позволяет сравнить дисперсию, вызванную различием между группами, с дисперсией, вызванной внутригрупповой изменчивостью. При истинности нулевой гипотезы (о равенстве средних в нескольких группах наблюдений, выбранных из генеральной совокупности), оценка дисперсии, связанной с внутригрупповой изменчивостью, должна быть близкой к оценке межгрупповой дисперсии. Если вы просто сравниваете средние в двух выборках, дисперсионный анализ даст тот же результат, что и обычный t-критерий для независимых выборок (если сравниваются две независимые группы объектов или наблюдений) или t-критерий для зависимых выборок (если сравниваются две переменные на одном и том же множестве объектов или наблюдений).

Сущность дисперсионного анализа заключается в расчленении общей дисперсии изучаемого признака на отдельные компоненты, обусловленные влиянием конкретных факторов, и проверке гипотез о значимости влияния этих факторов на исследуемый признак. Сравнивая компоненты дисперсии друг с другом посредством F—критерия Фишера, можно определить, какая доля общей вариативности результативного признака обусловлена действием регулируемых факторов.

Исходным материалом для дисперсионного анализа служат данные исследования трех и более выборок:, которые могут быть как равными, так и неравными по численности, как связными, так и несвязными. По количеству выявляемых регулируемых факторов дисперсионный анализ может быть однофакторным (при этом изучается влияние одного фактора на результаты эксперимента), двухфакторным (при изучении влияния двух факторов) и многофакторным (позволяет оценить не только влияние каждого из факторов в отдельности, но и их взаимодействие).

Дисперсионный анализ относится к группе параметрических методов и поэтому его следует применять только тогда, когда доказано, что распределение является нормальным.

Дисперсионный анализ используют, если зависимая переменная измеряется в шкале отношений, интервалов или порядка, а влияющие переменные имеют нечисловую природу (шкала наименований).

35. Понятие корреляцию Линейный коэффициент корреляции Пиросона: оценка достоверности, интерпретация

Корреляция (корреляционная зависимость) — статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения значений одной или нескольких из этих величин приводят к систематическому изменению значений другой или других величин. Математической мерой корреляции двух случайных величин служит корреляционное отношение либо коэффициент корреляции (или). В случае если изменение одной случайной величины не ведёт к закономерному изменению другой случайной величины, но приводит к изменению другой статистической характеристики данной случайной величины, то подобная связь не считается корреляционной, хотя и является статистической.

Коэффициент корреляции Пирсона характеризует существование линейной зависимости между двумя величинами.

Корреляция представляет собой меру зависимости переменных. Наиболее известна корреляция Пирсона. При вычислении корреляции Пирсона предполагается, что переменные измерены, как минимум, в интервальной шкале. Некоторые другие коэффициенты корреляции могут быть вычислены для менее информативных шкал. Коэффициенты корреляции изменяются в пределах от -1.00 до +1.00. Обратите внимание на крайние значения коэффициента корреляции. Значение -1.00 означает, что переменные имеют строгую отрицательную корреляцию. Значение +1.00 означает, что переменные имеют строгую положительную корреляцию. Отметим, что значение 0.00 означает отсутствие корреляции.

Наиболее часто используемый коэффициент корреляции Пирсона называется также линейной корреляцией, т.к. измеряет степень линейных связей между переменными.

Корреляция Пирсона (далее называемая просто корреляцией) предполагает, что две рассматриваемые переменные измерены, по крайней мере, в интервальной шкале. Она определяет степень, с которой значения двух переменных " пропорциональны" друг другу. Важно, что значение коэффициента корреляции не зависит от масштаба измерения. Например, корреляция между ростом и весом будет одной и той же, независимо от того, проводились измерения в дюймах и фунтах или в сантиметрах и килограммах. Пропорциональность означает просто линейную зависимость. Корреляция высокая, если на графике зависимость " можно представить" прямой линией (с положительным или отрицательным углом наклона).

36. Корреляционное отношение: назначение, оценка достоверности, установление криволинейности связи

При нелинейной кор. связи нелинейным изменениям одного признака соответствуют в среднем неравномерным, но подчиняющимся определенным закономерностям схемам другого признака.

Нелинейная связь возникает при заметном отклонении одного или обоих признаков от нормального распределения.

Для измерения нелинейной зависимости используют корреляционные отношения. Они принимают значение от 0 до 1.

Направленность связи опред. по кор. решетке или по графику.

До 0, 3 – слабая связь

0, 3 – 0, 5 – средняя сила

0, 5 – 0, 7 – значительная

0, 7 – 0, 9 – сильная

Выше 0, 9 – очень сильная

Кор. отношения описывают связь между признаками как двухсторонную

Первое кор. отношение показывает зависимость X от Y, второе – Y от X

Таким образом, для пары признаков могут быть рассчитаны два кор. отношения – прямое и обратное.

Как правило, отношения не совпадают. Чем сильнее связь, и чем ближе она к линейной, тем сильнее совпадают их значения. Как правило, на практике рассчитывают одно кор. отношение (исходя из их значимости).

Достоверность опред по Стьюденту или Фишеру.

Коэф. линейности – если достоверен, то связь криволинейна, если недостоверен – то прямолинейна.

37. Ранговый коэффициент корреляции Спирмена, множественный и частный коэффициенты корреляции

Существующие между явлениями формы и виды связей весьма разнообразны по своей классификации. Предметом статистики являются только такие из них, которые имеют количественный характер и изучаются с помощью количественных методов. Рассмотрим метод корреляционно-регрессионного анализа, который является основным в изучении взаимосвязей явлений.

Данный метод содержит две свои составляющие части — корреляционный анализ и регрессионный анализ. Корреляционный анализ — это количественный метод определения тесноты и направления взаимосвязи между выборочными переменными величинами. Регрессионный анализ — это количественный метод определения вида математической функции в причинно-следственной зависимости между переменными величинами.

Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0, 1 до 0, 3; умеренная — от 0, 3 до 0, 5; заметная — от 0, 5 до 0, 7; высокая — от 0, 7 до 0, 9; весьма высокая (сильная) — от 0, 9 до 1, 0. Она используется далее в примерах по теме.

38. Корреляции и причинность. Влияние неоднородности выборки и выбросов на коэффициент корреляции

КОРРЕЛЯЦИИ КОЭФФИЦИЕНТ -числовая характеристика совместного распределения двух случайных величин, выражающая их взаимосвязь. К. к. 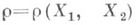для случайных величин Х ₁ и Х ₂ с математич. ожиданиями и ненулевыми дисперсиями

определяется равенством

К. к. для Х ₁ и Х ₂ совпадает с ковариацией для нормированных величин К. к. симметричен относительно X₁ и Х ₂ и инвариантен относительно изменения начала отсчета и масштаба. При этом Значение К. к. как одной из возможных мер взаимосвязи определяется следующими его свойствами: 1) если величины Х ₁ и Х ₂ независимы, то (обратное утверждение в общем случае неверно), о величинах, для к-рых говорят, что они некоррелированы; 2) тогда и только тогда, когда величины связаны линейной функциональной зависимостью:

Трудность интерпретации r как меры взаимозависимости заключается в том, что равенство r=0 может иметь место как для независимых, так и для зависимых случайных величин, в общем случае для независимости необходимо и достаточно равенство нулю их максимального коэффициента корреляции. Таким образом, К. к. не исчерпывает все виды связи между случайными величинами и является лишь мерой линейной зависимости. При этом степень линейной зависимости характеризуется следующим образом: величина

дает линейное представление X₂ по Х ₁, наилучшее в том смысле, что

39. Назначение регрессионного анализа, эмпирическая линия регрессии

40. Парная регрессия: расчёт параметров уравнения, графическая интерпретация, лианеризация

Парная регрессия (bivariate regression) — это метод установления математической (в форме уравнения) зависимости между одной метрической зависимой (критериальной) переменной и одной метрической независимой переменной (предиктором). Во многом этот анализ аналогичен определению простой корреляции между двумя переменными. Однако, для того чтобы вывести уравнение, мы должны одну переменную представить как зависимую, а другую — как независимую.

Парная регрессия.

• Прямой • Гиперболы • Параболы

Выбор уравнения регрессии.

1) можно определить зависимость графически;

2) если результативный и факторный признак возрастают одинаково, примерно в арифметической прогрессии – связь линейная; а при обратной связи –гиперболическая; если результативный признак увеличивается в арифметической прогрессии, а факторный - значительно быстрее, то используется параболическая или степенная регрессии.

Расчет параметров уравнения регрессии

(a 0, a1, a 2) осуществляется МНК (в основе которого

лежит предложение о независимости наблюдений исследуемой совокупности).

Основной принцип МНК: Линейная зависимость. Коэффициент эластичности. Криволинейная зависимость (парная регрессия). 1)Уравнение параболы второго порядка: 2) Уравнение гиперболы:

25. Вследствие разнообразия биологических объектов выборочная совокупность не может точно охарактеризовать генеральную. Всегда будут присутствовать расхождения или ошибки, которые называются ошибками репрезентативности (от лат. represento – представляю). Они возникают при оценке целого по его части. Эти ошибки не зависят от исследователя, их нельзя избежать, но можно и нужно учитывать в процессе статистической обработки результатов, например, для нахождения генеральных параметров достоверности.

Ошибка средней арифметической

Эта ошибка определяется по формуле:

, из которой видно, что чем больше разнообразие признака (величина σ), тем больше ошибка.

Если бы все объекты были одинаковы, то есть разнообразие было бы равно нулю, то и ошибка была бы равна нулю (m = 0). В этом случае даже один экземпляр точно характеризовал бы всю генеральную совокупность.

Ошибка также зависит от численности выборки n: чем больше численность, тем меньше ошибка. Определив ошибку репрезентативности m, можно найти генеральную среднюю по формуле:

Точное значение генеральной средней найти невозможно, поскольку число объектов стремится к бесконечности. С помощью данной формулы с определенной степенью вероятности находятся две границы: максимального и минимального значений. Эти значения называются доверительными интервалами, то есть такими, которым можно доверять.

Если доверительные интервалы определены с вероятностью 95% или 0, 95, то с вероятностью 5% (100% – 95%) или 0, 05 генеральная средняя может быть меньше минимального и больше максимального значений. Значение 5% (или 0, 05) называется уровнем значимости. Чаще всего в биологических и экологических исследованиях результат определяется с вероятностью 95% или 0, 95. Такой вероятности соответствует tst = 2.

Для уточнения стандартных значений t можно воспользоваться таблицей 1. В ней степень вероятности, выраженная в долях единицы, обозначается B. Всего представлено 4 степени вероятности. Из данных, приведенных в таблице видно, что при значениях ν больше 28, при вероятности 95% t = 2. Если значения ν меньше, то величина t постепенно увеличивается. При работе со средними арифметическими ν = n - 1. Этот показатель называется числом степеней свободы.

Коэффициент вариации (Coefficient of variation) — это отношение стандартного отклонения к среднему арифметическому, выраженное в процентах. Коэффициент вариации - это показатель относительной изменчивости переменной. Коэффиициент вариации имеет смысл только в случае, когда переменную измеряют по относительной шкале.

41. Парная регрессия: оценка достоверности параметров уравнения, адекватности модели, итоговые статистики

42. Множественная линейная регрессия: ограничения, уравнение, обоснование расчётов, анализ влияния факторов по коэффициентам регрессии и частным коэффициентам корреляции

Y=A+B1X+B2Z+B3Q

Коэффициент регрессии получают при решении систем нормальных уравнений.

Условия применения множественной линейной регрессии:

1. зависимые и независимые переменные должны распределяться нормально.

2. признаки должны быть независимы друг от друга (если нет, коэф. корреляции больше 0, 75(0, 8))

3. в готовой модели должно использоваться не более 8 факторов (переменных).

4. при расчете уравнения желательно, чтобы для отображения факторов использовались одноразрядные числа, при том если переменная выражена 4х-5 и более разрядным числом, то требуется уменьшить разряд этой переменной. (1945 – 45, 1941 – 41).

Если коэф. регрессии положителен, то при увеличении независимой переменной увеличивается и зависимая переменная.

Если коэф. регрессии отрицателен, то при увеличении зависимой переменной уменьшается независимая.

Коэф. регрессии показывает насколько изменится зависимая переменная при изменении независимой на ед.

Для изучения влияния независимых переменных на изменчивость зависимой переменной коэф. регрессии использовать нельзя, для этого используется частный коэф. корреляции.

Коэф. множественной корреляции рассчитывается для линиализованного уравнения, поэтому для каждой модели он свой.

43. Множественная линейная регрессия: оценка достоверности параметров уравнения, адекватности модели, итоговые статистики. Множественная нелинейная регрессия

После того, как рассчитали коэффициент регрессии определяют достоверны ли они с помощью t критерия Стьюдента, для этого коэф. регрессии делят на его ошибку.

tвыч больше tтаб, то коэф. регрессии достоверен.

tвыч меньше tтаб, не достоверно при заданном уровне значимости – модель непригодна.

При дальнейшем расчете модели фактор коэф. регрессии который недостоверен отбрасывается.

Оценка адекватности модели проводится путем сравнения дисперсии зависимой переменной, объясняемой с помощью модели и дисперсии не объясняемой моделью.

Множественная нелинейная регрессия (если нарушается 1е условие применения) чтобы превратить нелинейное уравнение в линейное проведя процедуру линеализации.

Y=A+B1Xв квадрате+B2Zв кубе+B3Qв четвертой

Хв квадрате = Х штрих Zв кубе = Z штрих Qв четвертой = Q штрих

Y=A+B1штрих +B2Zштрих +B3Qштрих

Y=AXв степени b1*Zв степени b2*Qв степени b3

Логарифм Y=логарифм A + b1*логарифм X + b2*логарифмZ + b3*логарифм Q

44. Классификация рядов динамики

Основным понятием в анализе динамических процессов является ряд динамики. Это последовательность значений статистического показателя, упорядоченного в порядке возрастания временного параметра (фактора времени).

Каждый ряд динамики содержит ряд элементов:

- значение времени

- соответствующее ему значение ряда (величина статистического показателя)

В качестве показателя времени в рядах динамики могут указываться определенные моменты времени, либо отдельные периоды (сутки, месяцы, годы).

Исходя из характера параметра ряда, ряды динамики бывают:

- моментные – уровни ряда характеризуют значения показателей по сост. на определенные моменты времени.

- интервальные – уровни ряда характеризуют значения показателей за определенный интервал.

Отличительной особенностью интервальных рядов абсолютных величин является возможность суммировать уровни, следующие друг за другом по периодам, поскольку их можно рассматривать как виток за длительный период.

Уровни рядов моментов рядов динамики суммировать не имеет смысла, поскольку суммирование будет включать одну и ту же величину, но разность уровней имеет определенный смысл.

Уровни динамики могут представлять собой относительные, абсолютные, и средние величины. Во 2-ом и 3-ем случае ряды динамики называются «производными».

Уровни этих рядов вычисляются на основе абсолютных показателей.

По полноте времени, отражаемого в рядах динамики, можно разделить на неполные и полные.

В полных рядах даты (периоды) следуют друг за другом с равными интервалами

В неполных рядах – последовательности времени в разных интервалах не соблюдаются.

45. Правила построения рядов динамики

Правила построения рядов динамики:

1) интервал между соседними уровнями ряда должен быть достаточного, и, желательного, одинакового размера.

Слишком большой интервал может скрыть существующие закономерности в динамике показателя, в результате, временной ряд может быть слишком коротким для некоторых видов анализа.

Недостаточно большой интервал увеличивает количество вычислений и приводит к обнаружению деталей, засоряющих общую тенденцию.

Размер интервала определяется, исходя из цели конкретного исследования.

2) уровни ряда должны быть сопоставимы, в противном случае измерение ряда динамики неправомерно.

Причины несопоставимости – изменение границ территории, к которой отнесёны те или другие показатели.

В большинстве случаев удаётся устранить несопоставимость путём перерасчёта более ранних значений показателей.

Процедура приведения уровней динамики к сопоставимому виду с помощью доп. Расчётов называется смыканием рядов динамики.

3) Аномальные значения (выбросы) должны исключаться из расчётов.

Уровни рядов динамики могут содержать аномальные (слишком большие или малые значения), появляющиеся либо в результате в сборе, передачи информации, либо являются реальным отображением процесса.

46. Средняя хронологическая

Для интервального ряда – y с черточкой сверху = y₁ + y₂ + y₃ +… +y_n / n

Где у – уровень ряда

Для одномоментного ряда:

y с черточкой сверху = 0, 5y₁ + y₂ + y₃ +… +0, 5y_n / n

47. Методы выравнивания рядов: укрупнение интервалов, средняя скользящая

Для выявления основных тенденций развития экологических процессов используются следующие методы выравнивания (сглаживания) рядов:

1) метод интервалов - используется в случае, если показатели за короткие промежутки времени, в силу влияния различных факторов, действующих на них, то повышаются, то понижаются. Из-за этого не видна основная тенденция развития изучаемого явления.

2) Метод скользящей средней – при данном методе уровни рядов заменяются средними уровнями, рассчитанных для последовательно-подвитных (скользящих) укрупненных интервалов, охватывающих М уровней рядов.

М – период, за который проводится расчёт средней скользящей.

48. Методы выравнивания рядов: аналитическое выравнивание

Для выявления основных тенденций развития экологических процессов используются следующие методы выравнивания (сглаживания) рядов:

Аналитическое выравнивание – более сложный метод обработки рядов с целью устранения случайных колебаний и выявления тренда.

Выравнивание уровня ряда по аналитическим формулам

Суть этого выравнивания заключается в замене эмпирических, т.е. фактических уровней теоретическими, которые рассчитаны по определенному уравнению.

При этом каждый фактический уровень рассматривается как сумма 2-ух составляющих – систематической, отражающей тренд, и выраженной опред. уравнением.

2 – ая составляющая – случайная величина, вызывающая колебания уровней вокруг тренда.

Задачи аналитического выравнивания:

- определение на основе аналитических данных вида математической функции, способной наиболее адекватно отразить тенденцию развития исследуемого показателя.

- нахождение по эмпирическим данным параметра указанной функции.

- расчёт по найденному уравнению теоретических (выровненных) уровней.

49. Выбор функции для динамической модели

В аналитических выравниваниях наиболее часто используют следующие функции:

- линейная функция

y = a₀ + a₁ * t (t – время, a₀ и a₁ – регрессионные коэффициенты)

- показательная функция

y = a₀ * a₁^t

- гиперболическая функция

y = a₀ + a₁ / t

- парабола 2-ого порядка

- ряд Фурье

Выбор той или иной функции осуществляется на основании графического изображения эмпирических данных, дополняемого содержательным анализом особенностей развития исследуемого показателя и специфики разных ф-й и их возможности отразить те или иные нюансы развития.

В качестве вспомогательных используются механические приёмы сглаживания (между интервалом и скользящей средней)

Частично устраняя случайные колебания, они помогают более точно определить тренд и выбрать адекватную модель. Если возможно использовать несколько моделей, то выбирают модель с наибольшим коэффициентом детерминации и с достоверным коэф. регрессии.

50. Автокорреляция в рядах динамики

Во многих рядах динамики можно наблюдать зависимость t-го уровня (y_t) от y_t-l (от предшествующего)

Например, урожай семян хвойной древесной породы за опред. год зависит, при прочих равных условиях, от урожая за предшествующие годы.

Урожайность с.х. культур в отдельные годы также может быть связана с урожайностью в предшествующие периоды.

Зависимость между последовательными (соседними) уровнями ряда динамики называется автокорреляцией.

В частности, если установить наличие автокорреляции, то эту зависимость можно выразить уровнем авторегрессии.

В отдельных случаях приходится устранять влияние автокорреляции на связь между исследуемыми показателями.

Измерить автокорреляцию между уровнями ряда можно с помощью коэф. автокорреляции, исчисляемого по формуле парного линейного коэф. корреляции Пирсона.

Коэф. корреляции можно рассчитывать между средними уровнями, либо между уровнями, сдвинутыми на любое число едениц времени.

Этот сдвиг, называемый временным лагом, определяет порядок коэффициента автокорреляции.

51. Проверка адекватности динамической модели. Критерий Дарбина-Уотсона

Применение модели в целях анализа и прогнозирования явлений возможно только после проверки адекватности, т.е. соответствию модели исследуемому процессу. Проверка адекватности модели строится на анализе остаточной компоненты.

Остаточная компонента получается после выделения из исследуемого ряда систематической составляющей, т.е. тренда и периодической составляющей., если периодическая составляющая присутствует во временном ряду.

Остаточная составляющая – это отклонение фактических значений временного ряда от расчетных значений.

Принято считать, что модель адекватна описываемому процессу, если остаточная последовательность представляет собой случайную компоненту ряда, то есть удовлетворяет следующим свойствам:

- с-во случайности колебаний уровня ряда

- соответствие остаточной компоненты нормальному закону с нулевым математическим ожиданием

- независимость значений остатков уровня ряда между собой

- если вид функций, описывающих систем. составляющую, выбран неудачно, то последовательность значения рядов остатков могут не соблюдать св-во независимости, так как могут коррелировать между собой. В этом случае говорят, что имеет место автокорреляция остатков.

Существует несколько способов обнаружения автокорреляции остатков:

1) критерий Дарбина – Уотсона

d = ∑ ⁿ_T=2 (e_t – e_t-1) / ∑ ⁿ_T=1 e_{t2 (квадрат)}

где

e_t – остаток текущего уровня ряда

e_t-1 – остаток предыдущего ряда

Применение критерия основано на сравнении расчетного значения статистики d с пороговыми значениями d_u и d_L

Граничное значение определяется по таблице, зависит от числа наблюдений и уровня значимости.

При сравнении расчётных значений с табличными возможны следующие варианты:

- если d расчётное меньше d нижнего d_L, то считается, что есть автокорреляция

- если d больше d_u, то считается, что автокорреляции нет

- если d находится в интервале между d_u и d_L, то вывод об отсутсвии или наличии автокорреляции подтвердить нельзя.

Если исследуется гипотеза о наличии автокорреляции, то с граничными значениями связывается величина 4-d, при условии, что d> 2

4-d < d_L – в этом случае имеет место отриц. автокорреляция

4-d > d_u – отриц. автокорреляции нет

Если 4-d в интервале между d_u и d_L, то нельзя сделать опред. вывод