
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Итерационные методы решения систем линейных алгебраических уравнений.
|
|
Решения, получаемые с помощью прямых методов, обычно содержат погрешности, вызванные округлениями при выполнении операций над числами. Рассмотрим методы, позволяющие уточнить решение, полученное с помощью прямого метода, либо самостоятельно получить это решение.
Первым шагом в итерационном методе является преобразование исходной системы  к виду
к виду
 , (3.1)
, (3.1)
где матрицы  и вектор
и вектор  определяются по матрице
определяются по матрице  и вектору
и вектору  . При этом обе системы являются эквивалентными, т.е. их решения совпадают. Вторым шагом является расстановка индексов в (3.1) и задание нулевого приближения, т.е.
. При этом обе системы являются эквивалентными, т.е. их решения совпадают. Вторым шагом является расстановка индексов в (3.1) и задание нулевого приближения, т.е.
 , (3.2)
, (3.2)
где  - заданный вектор. Оценка погрешности
- заданный вектор. Оценка погрешности  - го приближения определяется соотношением
- го приближения определяется соотношением
 , (3.3)
, (3.3)
где  - точное решение исходной системы.
- точное решение исходной системы.
Оценка (3.3) при заданном  позволяет осуществлять остановку итерационного процесса.
позволяет осуществлять остановку итерационного процесса.
Различные итерационные методы отличаются выбором матриц  и вектора
и вектора  .
.
Если  , то метод построения последовательных приближений (3.2) принято называть методом простых итераций. Известен следующий результат о сходимости метода простых итераций: если норма матрицы
, то метод построения последовательных приближений (3.2) принято называть методом простых итераций. Известен следующий результат о сходимости метода простых итераций: если норма матрицы  меньше единицы, то последовательные приближения
меньше единицы, то последовательные приближения
 (3.3)
(3.3)
сходятся к единственному решению системы  со скоростью геометрической прогрессии при произвольном векторе нулевого приближения
со скоростью геометрической прогрессии при произвольном векторе нулевого приближения  . Наиболее целесообразным в качестве компонент
. Наиболее целесообразным в качестве компонент  взять приближенные значения неизвестных, полученные грубой прикидкой либо прямыми методами.
взять приближенные значения неизвестных, полученные грубой прикидкой либо прямыми методами.
Таким образом, процесс сходится, если выполняется одно из условий:
 .
.
Если  < 1, то можно дать оценку погрешности метода простой итерации:
< 1, то можно дать оценку погрешности метода простой итерации:
 . (3.4)
. (3.4)
Оценка (3.4) называется априорной оценкой погрешности итерационного процесса, т.к. не проводя вычислений по  и
и  можно оценить погрешность
можно оценить погрешность  -го приближения
-го приближения  .
.
Можно показать, что если элементы матрицы  удовлетворяют одному из условий
удовлетворяют одному из условий
 ,
,
то процесс итерации сходится к точному решению системы  при любом
при любом  . Оценка погрешности этого приближенного решения
. Оценка погрешности этого приближенного решения  дается одной из формул:
дается одной из формул:


Приведение исходной системы  к виду
к виду 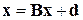 можно осуществить различными способами. Если диагональные элементы матрицы
можно осуществить различными способами. Если диагональные элементы матрицы  не равны нулю, т.е.
не равны нулю, т.е.  , то исходную систему можно записать в виде
, то исходную систему можно записать в виде
 . (3.5)
. (3.5)
В этом случае элементы матрицы  определяются следующим образом:
определяются следующим образом:
 . (3.6)
. (3.6)
Пример 3. Решить систему линейных уравнений

методом итераций с погрешностью, не превышающей  =0.01.
=0.01.
Решение. Используя выражения (3.5), (3.6) получим:
 .
.
Нормы матрицы  =0.82 и
=0.82 и  . Следовательно, выполнены условия сходимости алгоритма простой итерации. В дальнейшем, для определенности, будем использовать норму
. Следовательно, выполнены условия сходимости алгоритма простой итерации. В дальнейшем, для определенности, будем использовать норму  . Полагая в качестве нулевого приближения вектор
. Полагая в качестве нулевого приближения вектор  , выполним несколько последовательных шагов итерационного процесса в соответствии с выражением (3.3). Результаты расчетов приведены в таблице:
, выполним несколько последовательных шагов итерационного процесса в соответствии с выражением (3.3). Результаты расчетов приведены в таблице:
Таблица 3.1

| |||||||

| 2.114 | 3.157 | 3.632 | 3.848 | 3.946 | 4.011 | 4.024 |

| -0.15 | 0.324 | 0.541 | 0.640 | 0.685 | 0.715 | 0.721 |

| 1.913 | 0.870 | 0.395 | 0.179 | 0.081 | 0.016 | 0.003 |

| 4.483 | 3.014 | 2.027 | 1.363 | 0.916 | 0.414 | 0.187 |
Данные таблицы показывают, что требуемая точность вычислений  =0.01 достигается при
=0.01 достигается при  =16.
=16.
|
|