
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Построение математической модели трехуровневой иерархической системы: предприятие - отрасли - регион.
|
|
Математическая модель, как было уже замечено ранее, является одним из методов прогнозирования. В отличие от других методов прогнозирования, модель представляет не только более точные количественные характеристики, точность которых в последнее время еще повышается за счет применения более совершенной вычислительной и компьютерной техники, но и более объемно и полно, отражает структуру исследуемого объекта к взаимосвязи, т.е. дает более полное представление об объекте, направлении его развития. В приложении к региону в качестве математической модели предлагается векторная задача линейного программирования (ВЗЛП), моделирующая интересы-цели отдельных предприятий, отраслей и региона в целом. Математическая модель представлена как трехуровневая иерархическая система (предприятия - отрасль - регион):
Opt Fr(X(t))={opt F1(Xr(t)) = {fкп (Xп(t)), к=  п, п=
п, п=  o, o=
o, o=  r }, (13.1.1)
r }, (13.1.1)
opt F2(Xr(t))={fко(Xo(t))= 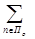 fкп(Xп(t)), к=
fкп(Xп(t)), к=  o, Ko=
o, Ko=  Kп, o=
Kп, o=  r }, (13.1.2)
r }, (13.1.2)
opt F3(Xr(t))={fк(Xr(t))=  fко(Xo(t)), к=
fко(Xo(t)), к=  r, Kr=
r, Kr= 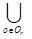 Ko }}, (13.1.3)
Ko }}, (13.1.3)

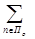
 å aijxj(t) £ bi, iÎ M, (13.1.4)
å aijxj(t) £ bi, iÎ M, (13.1.4)
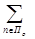
 aijxj(t) £ bi, i Î Mo, o=
aijxj(t) £ bi, i Î Mo, o=  r, (13.1.5)
r, (13.1.5)
 aijxj(t)£ bi, i Î Mп, п=
aijxj(t)£ bi, i Î Mп, п=  o, o=
o, o=  r, (13.1.6)
r, (13.1.6)
xj(t)£ uj(t), j=  п, п=
п, п=  o, o=
o, o=  r, " rÎ R, (13.1.7)
r, " rÎ R, (13.1.7)
где 1) Xr(t) ={Xо(t)= {Xп(t)= {Xj (t), j=  п}, п=
п}, п=  o, o=
o, o=  r} " rÎ R - вектор неизвестных определяет объемы продукции, выпускаемой в регионе, в его отраслях, которые представлены пÎ Пo предприятиями соответственно, здесь Nп, Пo, Or - множество индексов видов продукции, выпускаемых на предприятиях; предприятий, входящих в отрасль; отраслей, входящих в исследуемый регион соответственно.
r} " rÎ R - вектор неизвестных определяет объемы продукции, выпускаемой в регионе, в его отраслях, которые представлены пÎ Пo предприятиями соответственно, здесь Nп, Пo, Or - множество индексов видов продукции, выпускаемых на предприятиях; предприятий, входящих в отрасль; отраслей, входящих в исследуемый регион соответственно.
2) Критерий региона. Он состоит из трех векторных критериев, определяющих цель развития региона: а) Векторный критерий:
F1(Xr(t))={fkп(X(t))=  cjkxj(t), k=
cjkxj(t), k=  п, п=
п, п=  o, o=
o, o=  r}, " rÎ R -
r}, " rÎ R -
определяет величину компонент k=  п техническо-экономических показателей (ТЭП) любого из предприятий пÎ Пo; cik - коэффициент, характеризующий единицу j-го вида продукции по k-му ТЭП;
п техническо-экономических показателей (ТЭП) любого из предприятий пÎ Пo; cik - коэффициент, характеризующий единицу j-го вида продукции по k-му ТЭП;
б) Векторный критерий:
F2(Xr(t))={fко(Xo(t))= 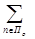
 cjkxj (t), к=
cjkxj (t), к=  o, Ko=
o, Ko=  Kп, o=
Kп, o=  r},
r},
представляет цели функционирования каждой отрасли.
Векторный критерий F2(Xr(t)) из (13.1.2), с одной стороны, функционально зависит от объемов продукции, выпускаемой отраслью в целом Xo, с другой, от ТЭП предприятий:
fко(Xo(t))=f (fкп(Xп(t)), к=  o, (13.1.8)
o, (13.1.8)
Предполагая линейную зависимость в (13.1.8), получим:
fко(Xo(t))= 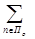 cкпfкп(Хп(t)), к=
cкпfкп(Хп(t)), к=  o, Ko=
o, Ko=  Kп, o=
Kп, o=  r, (13.1.9)
r, (13.1.9)
где cкп, пÎ П - коэффициенты агрегации ТЭП предприятий.
в) Векторный критерий:
F3(Xr(t))={fк(Х(t))= 
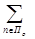
 cjkxj(t), к=
cjkxj(t), к=  r, Kr=
r, Kr= 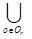 Ko},
Ko},
каждая компонента которого представляет ТЭП региона. Векторный критерий fк(Х(t)), функционально зависит от ТЭП отрасли:
fк(Х(t)) = f(fко(Xo(t)), к=  o). (13.1.10)
o). (13.1.10)
Предполагая линейную зависимость в (13.1.10), получим
fк(Х(t))=  cok fко (Хo(t)), к=
cok fко (Хo(t)), к=  r, Kr=
r, Kr= 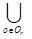 Ko, (13.1.11)
Ko, (13.1.11)
где cоk - коэффициент агрегации отраслей, Кп, Ko, Kr- множество индексов (число) критериев предприятий, отрасли и региона в целом соответственно.
3) Ограничения: а) накладываемые на деятельность региона в целом (13.1.4), связаны с финансовыми и дефицитными ресурсами. Эти ресурсы регион распределяет между отраслями; б) накладываемые на деятельность отрасли oÎ O (13.1.5), связаны с природными ресурсами, перераспределением трудовых ресурсов; в) ограничения, накладываемые на деятельность предприятий (13.1.6), (материальные и трудовые ресурсы, производственные фонды): г) (13.1.7) - ограничения, связанные с рыночной потребностью в j-ом виде продукции, производимой в регионе.
|
|