
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Типовые задачи прогнозирования
|
|
Модель межотраслевого баланса используется в краткосрочном и среднесрочном прогнозировании (индикативном планировании) для многовариантных расчетов сбалансированного развития экономики региона. Выделим три типовые задачи. [51].
1. Определение сбалансированных выпусков отраслей, обеспечивающих задаваемые варианты конечного спроса(КС) -Y. Для решения данной задачи используется система уравнений:
X = (I - A)-1Y, (12.6.20)
RX  B, (12.6.21)
B, (12.6.21)
Xj  Мj, j =
Мj, j =  . (12.6.22)
. (12.6.22)
Меняя значения векторов Y={yj, j =  }, получим валовые выпуски отраслей - X={xj, j =
}, получим валовые выпуски отраслей - X={xj, j =  }. При этом учитываются ограничения по производственным ресурсам (12.6.21) и мощностям (12.6.22).
}. При этом учитываются ограничения по производственным ресурсам (12.6.21) и мощностям (12.6.22).
Варианты конечного спроса должны соответствовать определенным целям экономического развития региона: увеличение и улучшение структуры конечного потребления домохозяйств, расширение государственных расходов, переход на более интенсивный инвестиционный режим и т.д.
Пример 9. Определение сбалансированных выпусков отраслей
2. Определение объемов конечного спроса исходя из заданных выпусков.
Для решения данной задачи используется система уравнений:
Y = (I - A)X, (12.6.23)
RX  B, (12.6.24)
B, (12.6.24)
Xj  Мj, j =
Мj, j =  . (12.6.25)
. (12.6.25)
Величина Y={yj, j =  } находится путем подстановки заданных величин X={xj, j =
} находится путем подстановки заданных величин X={xj, j =  } в каждое уравнение. Предпочтительный вектор Y находится путем сопоставления серии векторов Х0.
} в каждое уравнение. Предпочтительный вектор Y находится путем сопоставления серии векторов Х0.
Пример 10. Определение объемов конечного спроса, исходя из заданных выпусков.
3. Расчеты сбалансированных объемов и конечного спроса смешанным составом неизвестных.
Анализ ситуации в структуре экономики региона позволяет выявить, что в одних отраслях объемы выпуска зависят от спроса, а в других - лимитируются производственными возможностями. Поэтому в прогнозных расчетах наряду с типовыми задачами 1 и 2 целесообразно использовать задачу, в которой по одним отраслям неизвестными являются величины хi, а по другим - yi. Сформулируем задачу прогнозных расчетов по модели межотраслевого баланса со смешанным составом переменных.
Пусть все отрасли разбиваются на две группы:
отрасли (их число - m), по которым неизвестными являются выпуски - вектор Х1, а задаются величины конечного спроса - вектор Y1 = D1;
отрасли (их число (n-m)), по которым задаются выпуски - вектор X2 = Q2, а неизвестными являются объемы КС - вектор Y2. Соответственно матрица А после перегруппировки отраслей приводится к блочному виду: А =  . Решение системы уравнений МОБ относительно X1 и Y2 возможно в следующей последовательности. Вначале решается подсистема порядка m:
. Решение системы уравнений МОБ относительно X1 и Y2 возможно в следующей последовательности. Вначале решается подсистема порядка m:
(I - A11)X1 = D1 + A12Q2, (12.6.26)
Находится вектор Х1, который подставляется в подсистему порядка (n-m):
Y2 = (I - A22)Q2 - A21X1, (12.6.27)
Каждое уравнение в этой подсистеме содержит только по одной неизвестной (yi) и решается независимо.
Пример 11. Расчеты сбалансированных объемов и конечного спроса смешанным составом неизвестных.
12.7. Информационные методы моделирования экономики региона на основе межотраслевого баланса[6]
Одним из методов определения эффективности работы отраслей края является составление и исследование (моделирование) межотраслевого баланса региона.
В ходе экономического моделирования решались следующие задачи:
1. Рассчитывался межотраслевой баланс Приморского края за 2004 г. по данным статистической отчетности, [72];
2. В соответствии с основными соотношениями и свойствами моделирассчитывались матрица прямых и полных затрат, а по ограничениям имеющихся трудовых ресурсов - коэффициенты полных трудовых затрат;
3. Проведен анализ взаимосвязей выпусков, производственных ресурсов и конечного спроса в крае и представлены типовые задачи прогнозирования;
4. На основании расчетов была построена и проанализирована модель межотраслевых зависимостей цен и добавленной стоимости, с изучением межотраслевых зависимостей конечного спроса и добавленной стоимости;
5. Был проведен анализ межотраслевой модели с открытыми внешними связями и изучено их влияние на экономику Приморского края.
6. Проведен расчет межотраслевой модели, представленной в виде оптимизационной задачи [48].
7. Проведен расчет межотраслевой модели, представленной в виде векторной задачи математического программирования [55]
Каждый этап представлен примерами, теоретическая часть которых рассмотрена в предыдущем разделе.
12.7.1. Построение и анализ модели межотраслевого баланса экономики (на примере Приморского края 2004 года)
Пример 1. Формирование межотраслевого баланса Приморского края.
Дано. Межотраслевой баланс экономики Приморского края за 2004 год, составлен на основе статистических данных и представлен в разрезе шести групп отраслей (секторов): «Промышленность», «Сельское хозяйство», «Строительство», «Лесное хозяйство», «Услуги», «Транспорт» (табл. 12.2).
Сектор «Промышленность» включает следующие отрасли: электроэнергетика, угольная промышленность, черная металлургия, цветная металлургия, горно-химическая промышленность, рыбное хозяйство, машиностроение и металлообработка, деревообрабатывающая и целлюлозно-бумажная промышленность, промышленность строительных материалов, легкая промышленность, пищевая промышленность.
Таблица 12.2
Межотраслевой баланс экономики Приморского края за 2004 г., мл. руб.
| Выпуск Затраты | Промежуточное потребление | Конечное использование | Всего
Xi, i= 
| ||||||||||
| Промышлен. | С/х | Строительство | Лесн. хоз-во | Услуги | Транспорт | Итого AX | Конеч. потребление | Вал. накопление | Тов. запасы | Экспорт | Итого Y | ||
| Промышлен. | |||||||||||||
| С/х | |||||||||||||
| Строительство | |||||||||||||
| Лес. хоз-во | |||||||||||||
| Услуги | |||||||||||||
| Транспорт | |||||||||||||
| Итого | |||||||||||||
| Опл.труда–Z1 | |||||||||||||
| Налоги–Z2 | |||||||||||||
| Амортизац.–Z3 | |||||||||||||
| Прибыль–Z4 | |||||||||||||
| ВДС – Z | |||||||||||||
Всего ресурс.
Xj, j= 
| |||||||||||||
| Занято, тыс.ч. | 61, 1 | 3, 6 | 83, 2 | 534, 7 | 974, 6 |
Сектор «Услуги» включает отрасли: связь, торговля, общественное питание, материально-техническое снабжение и сбыт, информационно-вычислительное обслуживание, операции с недвижимым имуществом, общая коммерческая деятельность по обеспечению функционирования рынка, жилищное хозяйство, коммунальное хозяйство и бытовое обслуживание, здравоохранение, физическая культура, социальное обеспечение, образование, культура и искусство, наука и научное обслуживание, финансы, кредит, страхование и пенсионное обеспечение, управление, геология и разведка недр, геодезическая и гидрометеорологическая служба.
Сельское хозяйство, строительство, лесное хозяйство и транспорт выделены в отдельные сектора для того, чтобы проследить динамику их развития и определить их вклад и социально-экономическое положение Приморского края.
Пример 2. Расчет коэффициентов прямых затрат.
Исходными данными для построения межотраслевого баланса являются данные Госкомстата России [16]. В модель межотраслевого баланса экономики Приморского края за 2004 год изображенного в таблице 13.1 введем математические переменные: Х1 – выпуск сектора «промышленность», Х2 – выпуск сельского хозяйства, Х3 – выпуск отрасли «строительство», Х4 – выпуск лесного хозяйства, Х5 – выпуск услуг, Х6 – выпуск транспорта.
Соответственно, у1, у2, у3, у4, у5, у6 – конечный спрос отраслей;
 х11 х12 х13 х14 х15 х16
х11 х12 х13 х14 х15 х16
х21 х22 х23 х24 х25 х26
х31 х32 х33 х34 х35 х36 промежуточное потребление отраслей.
х41 х42 х43 х44 х45 х46
х51 х52 х53 х54 х55 х56
х61 х62 х63 х64 х65 х66
Суть коэффициентов промежуточного потребления заключается в следующем: например, коэффициент х11 показывает, какой объем выпуска промышленности был потрачен в промышленности при производстве продукции; коэффициент х12 показывает объем продукции промышленности, потраченный в сельском хозяйстве и т.д. Отсюда по строкам первого квадранта межотраслевого баланса «Промежуточное потребление», представляющий выпуск продукции каждой отрасли показано, как он (выпуск) распределяется между всеми отраслями, т.е. изображены взаимосвязи отраслей экономики региона.
Требуется определить.
1) Построить на EXCEL межотраслевой баланс, на основе табл. 13.1.
2) Рассчитать коэффициенты прямых затрат по формуле aij = xij / Xi.
3) Выполнить проверку расчета коэффициентов прямых затрат.
4) Рассчитать коэффициенты полных затрат по формуле В=(I-A)-1.
5) Выполнить проверку расчета коэффициентов полных затрат.
Решение.
В базовой модели МОБ используется допущение о пропорциональной зависимости между затратами и объемом производства, т.е. вводятся линейные однородные функции производственных затрат.
Рассчитаем на основе МОБ (12.6.4) матрицу коэффициентов прямых затрат А={aij}, где aij - коэффициенты прямых затрат продукции произведенной i-ой отраслью идущей на производство единицы продукции j-ой отрасли. Коэффициенты матрицы А получены путем деления промежуточного потребления на валовой выпуск: aij = xij / Xi. В результате получим матрицу А:
А =  X =
X = 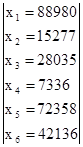 , Y=
, Y=  .
.
К ней добавим вектор выпуска продукции Х=АX+Y и вектор конечного использования Y=(I-А)*X, где

 1 0 0 0 0 0
1 0 0 0 0 0
0 1 0 0 0 0
I= 0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0
0 0 0 0 0 1 - единичная матрица.
Для проверки коэффициентов aij составим систему уравнений материального межотраслевого баланса, которая примет следующий вид:
Х1=0, 28х1+0, 44х2+0, 307х3+0, 075х4+0, 121х5+0, 082х6+у1;
Х2=0, 075х1+0, 042х2+0, 012х3+0, 076х4+0, 009х5+0, 014х6+у2;
Х3=0, 014х1+0, 063х2+0, 04х3+0, 087х4+0, 011х5+0, 019х6+у3;
Х4=0, 0005х1+0, 003х2+0, 0017х3+0, 004х4+0, 0002х5+0, 0004х6+у4;
Х5=0, 174х1+0, 087х2+0, 199х3+0, 373х4+0, 056х5+0, 145х6+у5;
Х6=0, 056х1+0, 068х2+0, 2611х3+0, 229х4+0, 012х5+0, 02х6+у6,
или
0, 72х1-0, 44х2-0, 307х3-0, 075х4-0, 121х5-0, 082х6=у1; (12.7.1)
-0, 75х1+0, 95х2-0, 012х3-0, 076х4-0, 009х5-0, 014х6=у2; (12.7.2)
-0, 014х1-0, 063х2+0, 967х3-0, 087х4-0, 011х5-0, 019х6=у3; (12.7.3)
-0, 0005х1-0, 003х2-0, 0017х3+0, 995х4-0, 0002х5-0, 0004х6=у4; (12.7.4)
-0, 174х1-0, 087х2-0, 199х3-0, 373х4+0, 943х5-0, 145х6=у5; (12.7.5)
-0, 056х1-0, 068х2-0, 2611х3-0, 229х4-0, 012х5+0, 979х6=у6, (12.7.6)
Пример 3. Расчет суммы коэффициентов прямых материальных затрат в матрице межотраслевого баланса Приморского края.
SummaKoefStolb=[0.5370 0.7056 0.8226 0.8468 0.2119 0.2819]
Матрица А является продуктивной, поскольку суммы коэффициентов aij по столбцам составляют: промышленность – 0, 537; сельское хозяйство – 0, 7056; строительство – 0, 8226; лесное хозяйство – 0, 8468; услуги – 0, 2119; транспорт – 0, 2819. Как видно, все они меньше единицы. Это является достаточным условием продуктивности матрицы коэффициентов прямых затрат.
Пример 4. Расчет матрицы коэффициентов полных затрат.
Экономический смысл коэффициентов bij, образующих матрицу B=(I-A)-1 состоит в том, что они определяют объем выпуска отрасли i, необходимый для получения единицы конечного спроса отрасли j. Коэффициенты полных затрат bij дают ценную информацию о структурных зависимостях между компонентами конечного спроса (потребление, накопление, вывоз т. д.) и необходимыми для их обеспечения объемами выпусков.
Матрица будет иметь следующий вид:
В=(I-A)-1 = 
Коэффициенты полных затрат существенно превышают коэффициенты прямых затрат. Сумма коэффициентов полных затрат по столбцам SummaB_KoefStolb =[1.9210 2.3253 2.3782 2.3937 1.3796 1.4687] показывают потребности в валовом выпуске на единицу конечного спроса каждой отрасли. Наибольший прирост валового выпуска дает увеличение конечного спроса на продукцию отрасли выпуск лесного хозяйства (мультипликатор равен 2, 3937).
В соответствии с (12.6.6) систему уравнений условного межотраслевого баланса можно представить в виде:
x1 = 1.4798y1 + 0.7521y2+0.5756y3+0.3389y4+0.2073y5+0.1778y6,
x2 = 0.0164y1+ 1.0566y2+0.0276y3+0.0943y4+0.0134y5+0.0192y6,
x3 = 0.0283y1+ 0.0872y2+1.0631y3+0.1153y4+0.0175y5+0.0274y6,
x4 = 0.0010y1+0.0047y2+0.0025y3+1.0055y4+0.0005y5+0.0007y6,
x5 = 0.2973y1+0.2799y2+0.3853y3+0.5403y4+1.1086y5+0.2011y6,
x6 =0.0982y1+0.1448y2+0.3242y3+0.2994y4+0.0323y5+1.0425y6.
Величины xi находятся путем подстановки в уравнение значений yi.
Например:
x1=1.479*53388+0.7521*3520+0.5756*5607+0.3389*220+0.2073*35451+0.1778*16861=88980,
x2=0.016*53388+1.0566*3520+0.0276*5607+0.0943*220+0.0134*35451+0.0192*16861=15277,
x3=0.028*53388+0.0872*3520+1.0631*5607+0.1153*220+0.0175*35451+0.0274*16861=28035,
x4=0.001*53388+0.0047*3520+0.0025*5607+1.0055*220+0.0005*35451+0.0007*16861=7336,
x5=0.297*53388+0.2799*3520+0.3853*5607+0.5403*220+1.1086*35451+0.2011*16861=72358,
x6=0.098*53388+0.1448*3520+0.3242*5607+0.2994*220+0.0323*35451+1.0425*16861=42136.
В системе Matlab эти уравнения примут вид: X=B*Y.
Анализируя модель межотраслевого баланса, определим пропорции отношений конечного спроса к валовому выпуску в процентном выражении:
Конечный спрос (промышленность)=  =
=  =40%.
=40%.
В итоге получим: промышленность направляла на конечный спрос 40% своего выпуска, сельское хозяйство – 77%, строительство – 80%, лесное хозяйство – 97%, услуги – 50, 7%, транспорт – 46, 8%.
Используя матрицу коэффициентов полных затрат, можно установить распределение выпусков отраслей, необходимых для обеспечения их конечного спроса (табл. 13.2).
Рассматривая отдельно компоненты конечного спроса, можно вывести следующие соотношения: промышленность направляла на валовое накопление основных фондов около 4% своего выпуска, сельское хозяйство – 4, 8%, строительство – 13, 8%, лесное хозяйство –7%, услуги – 1, 3, транспорт – 15, 5%.
Таблица 13.2
Распределение выпуска отраслей на обеспечение их конечного спроса, %
| Отрасли | Пром-ть | С/х | Строительство | Лесное хоз-во | Услуги | Транспорт |
| Пром-ть | 43, 5 | 9, 4 | 15, 0 | 2, 1 | 21, 0 | 9, 0 |
| С/х | 3, 2 | 72, 0 | 1, 5 | 5, 7 | 15, 0 | 2, 6 |
| Строительство | 25, 3 | 6, 1 | 31, 0 | 12, 2 | 14, 7 | 10, 7 |
| Лесное хоз-во | 13, 5 | 3, 4 | 19, 8 | 37, 2 | 6, 1 | 20, 0 |
| Услуги | 9, 7 | 12, 7 | 17, 2 | 6, 3 | 48, 6 | 5, 5 |
| Транспорт | 14, 5 | 7, 1 | 16, 8 | 5, 6 | 11, 2 | 44, 8 |
| Итого |
Распределение выпуска, идущего на конечное потребление: промышленность – 22% выпуска, сельское хозяйство – 60%, строительство – 41, 5%, лесное хозяйство –67%, услуги – 35, 7, транспорт – 22%.
Пример 5. Расчет полных затрат труда в межотраслевом балансе.
Анализируя модель межотраслевого баланса и распространив предположение о пропорциональности затрат и объемов производства на множество ограниченных ресурсов, можно рассчитать коэффициенты прямых, полных и косвенных трудовых затрат.
Таким образом, коэффициенты прямых трудовых затрат, определяемые отношением числа занятых в данной отрасли и ее валовым выпуском, примут соответствующий вид:
t=[Tz(1)/X(1) Tz(2)/X(2) Tz(3)/X(3) Tz(4)/X(4) Tz(5)/X(5) Tz(6)/X(6)]
t = (2.2477 6.0221 2.1794 0.4907 1.1498 12.6899).
SuTz=sum(Tz) =974600.
Коэффициенты полных трудовых затрат представляют собой суммы затрат живого труда (прямые затраты) и овеществленного труда (косвенные затраты) на единицу произведенной продукции. Используя матрицу коэффициентов полных затрат В и неравенство r(I-A)-1≤ R, получим: T=t*B, где Т – матрица коэффициентов полных трудовых затрат.
T = (5.0748 10.4047 8.3345 6.4952 2.2694 14.0353).
Коэффициенты косвенных трудовых затрат равны: T1 = T-t
T1 = (2.8271 4.3826 6.1551 6.0045 1.1196 1.3454)
Отношение полных трудовых затрат к прямым:
T2 =Kz=[Tj(1)/t(1) Tj(2)/t(2) Tj(3)/t(3) Tj(4)/t(4) Tj(5)/t(5) Tj(6)/t(6)].
T2 = (2.2578 1.7278 3.8242 13.2358 1.9737 1.1060)
В таблице 13.3 изображено распределение занятости между выпусками продукции.
Таблица 13.3
Распределение занятости между выпусками и конечным спросом отраслей, %
| Отрасли | На выпуск продукции | На конечный спрос |
| Промышленность | 54, 9 | |
| Сельское хозяйство | 9, 4 | |
| Строительство | 6, 3 | |
| Лесное хозяйство | 0, 4 | |
| Услуги | 8, 5 | |
| Транспорт | 20, 5 | |
| Итого |
Пример 6. Распределение выпуска на обеспечение конечного спроса отраслей.
Неотъемлемой частью анализа модели МОБ региона является установление зависимостей выпусков отраслей и затрат производственных ресурсов от отраслевой структуры конечного спроса. По статистическим данным Приморского края вектор-столбец отраслевой структуры конечного спроса имеет вид:

 α = 0.3470 0.1146 0.2186 0.0694 0.3598 0.2466 Т
α = 0.3470 0.1146 0.2186 0.0694 0.3598 0.2466 Т
Вектор-столбец выпусков, необходимых для получения общего объема конечного спроса рассчитывается по формуле: β = (I-A)-1*α или β = В*α:



 1.4769 0.1291 0.1814 0.0279 0.01684 0.0842 0.3470
1.4769 0.1291 0.1814 0.0279 0.01684 0.0842 0.3470
0.0955 1.0566 0.0506 0.0453 0.0637 0.0530 0.1146
β = 0.0898 0.0475 1.0631 0.0301 0.0450 0.0412 * 0.2186
0.0122 0.0098 0.0095 1.0055 0.0046 0.0038 0.0694
0.3650 0.0591 0.1490 0.0547 1.1070 0.1170 0.3598
0.2073 0.0524 0.2156 0.0521 0.0554 1.0424 0.2466
Таким образом, на 1000 рублей общего объема КС требуется производить продукции отрасли «промышленность» на 347 рублей, отрасли «сельское хозяйство» - на 114, 6 рублей, отрасли «строительство» - 218, 6 рублей, «лесное хозяйство» - 69, 4 рубля, «услуги» - 359, 8 рублей, «транспорт» - 246, 6, а валовой выпуск должен составить 1356 рублей.
Такие же параметры можно вычислить по данным таблицы МОБ, деля выпуски отраслей на общий объем КС. Однако предыдущая формула более универсальна – она позволяет находить коэффициенты β при меняющемся векторе α, что часто используется в экономическом анализе.
Для определения потребности в трудовых ресурсах на единицу общего объема конечного спроса, необходимо использовать следующее произведение: g = T*α.

 g = (0.0057 0.0074 0.0033 0.0006 0.0042 0.0144) *
g = (0.0057 0.0074 0.0033 0.0006 0.0042 0.0144) *

 0.3470 0.008 0.1146 0.2186 0.0694 0.3598 0.2466 т = 0.008
0.3470 0.008 0.1146 0.2186 0.0694 0.3598 0.2466 т = 0.008
Можно также получить из таблицы межотраслевого баланса, путем деления общей занятости на общий объем конечного спроса 974, 6/139091, 8. Отсюда потребность в трудовых ресурсах на единицу общего объема конечного спроса составляет 0, 008 или 8 человек на 1000 рублей конечного спроса.
Таким образом, составление и изучение межотраслевого баланса, а также расчет с помощью него различных экономических показателей, дает возможность анализировать и прогнозировать экономическую ситуацию в регионе.
Пример 7. Потребность в трудовых ресурсах на единицу общего объема конечного спроса.
|
|