
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Модель процесса обучения как цепь Маркова
|
|
Рассмотрим еще один пример вероятностного моделирования информационного процесса. На рисунке 6.7 представлена цепь Маркова, моделирующая процесс прохождения обучаемым фрагмента некоторого учебного курса и содержащая десять узлов, соответствующих различным шагам процесса обучения [21 ].
В модели на рисунке 6.7 выделены следующие состояния: S1 – изучение первого раздела (модуля) теоретического материала; S2, S3 – ответы на вопросы по первому разделу; S4 – изучение материала второго раздела (по этому разделу не предусмотрен контроль); S5 - изучение теоретического материала третьего раздела; S6 – S9 - ответы на вопросы по третьему разделу; S10 – завершение изучения третьего раздела. Из рисунка видно, что состояния S1 – S9 относятся к множеству невозвратных состояний, S10 - поглощающее состояние.
| S1 |
| S3 |
| S2 |
| S5 |
| S6 |
| S7 |
| S8 |
| S9 |
| S10 |
| S4 |
| 0, 9 |
| 0, 25 |
| 0, 2 |
| 0, 2 |
| 0, 22 |
| 0, 45 |
| 0, 25 |
| 0, 45 |
| 0, 65 |
| 0, 7 |
| 0, 7 |
| 0, 3 |
| 0, 2 |
| 0, 65 |
| 0, 22 |
| 0, 22 |
| 0, 75 |
| 0, 7 |
| 0, 15 |
| 0, 1 |
| 0, 1 |
| 0, 1 |
| 0, 1 |
| 0, 12 |
| 0, 1 |
| 0, 1 |
| 0, 1 |
| 0, 1 |
Рисунок 6.7 Цепь Маркова, моделирующая процесс прохождения фрагмента учебного курса
Заданы оценки трудоемкостей прохождения каждого узла:
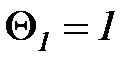 час,
час, 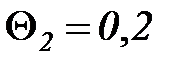 час,
час, 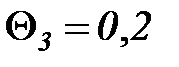 час,
час,  час,
час,
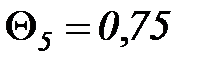 час,
час, 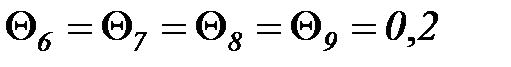 час.
час.
Матрица вероятностей переходов 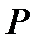 имеет вид:
имеет вид:

Начальное распределение вероятностей 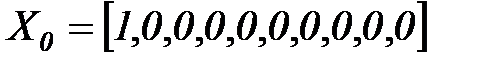 означает, что процесс обучения всегда стартует из первого состояния.
означает, что процесс обучения всегда стартует из первого состояния.
Средние значения числа пребываний процесса в множестве невозвратных состояний, вычисленные по формуле (6.29), задаются следующей матрицей:

Средняя трудоемкость процесса:
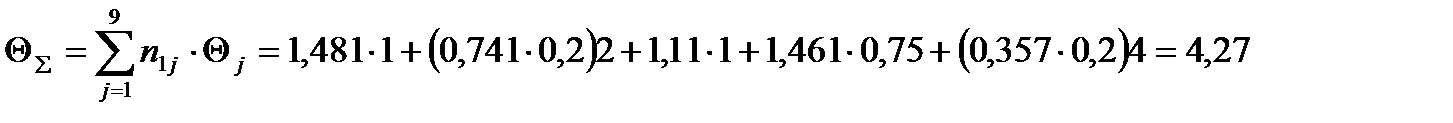 часов.
часов.
Вычислив матрицу дисперсий D по формуле (6.31) и взяв значения элементов первой строки, соответствующей стартовому состоянию процесса, получим среднеквадратичное отклонение трудоемкости процесса от средней
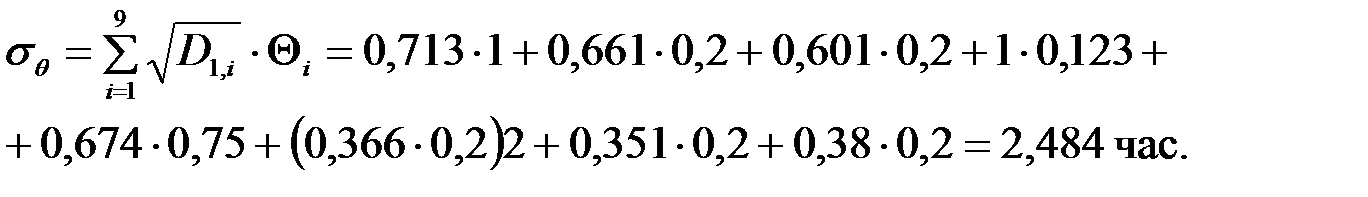
На рисунке 6.7 приведен график распределения вероятностей прохождения отдельных этапов курса, рассчитанный по формуле (6.29). Из него, в частности видны вероятности завершения процесса за заданное число шагов (переход в состояние S10). Из рисунка 6.6 видно, что минимальное число шагов, необходимое для завершения фрагмента курса, равно 5. Вероятность такого исхода, согласно рисунку 6.88, равна 0, 337, а достаточно надежное завершение курса наступает на 9 – 13 шагах.
 Рисунок 6.8 Вероятности пребывания процесса в каждом из состояний
Рисунок 6.8 Вероятности пребывания процесса в каждом из состояний
6.7 Непрерывно-стохастические модели (Q – модели)
Как отмечалось в начале данной главы, наиболее известным классом Q –моделей являются модели массового обслуживания. Задачи массового обслуживания возникают в тех случаях, когда требования на выполнение работ поступают в случайные моменты времени, а осуществление этих работ, называемое обслуживанием, производится одним или несколькими обслуживающими устройствами. Длительность выполнения отдельных требований также является случайной величиной. Системы, осуществляющие обслуживание поступающих требований в указанном режиме, называют системами массового обслуживания.
Устройство, способное в любой момент времени обслужить лишь одно требование, называют каналом обслуживания. При наличии нескольких каналов, способных одновременно обслужить ряд требований, говорят о многоканальной системе.
Характерной особенностью задач массового обслуживания является возникновение несоответствия между скоростью поступления требований и скоростью обслуживания, в результате этого – либо некоторые устройства простаивают, либо возникают очереди на обслуживание. С подобными ситуациями приходится сталкиваться постоянно: люди стоят в очередях у касс и прилавков магазинов, в залах регистрации аэропортов; самолеты ждут, когда освободится взлетная полоса; владельцы автомобилей ждут обслуживания в автоцентрах и т.д. При этом принципиальный интерес представляют следующие характеристики системы массового обслуживания:
· длина очереди в различные моменты времени и ее средняя длина,
· общая продолжительность нахождения требования в системе обслуживания (ожидание в очереди и само обслуживание),
· доля времени, в течение которого обслуживающие устройства не были заняты.
Для получения математической модели системы массового обслуживания необходимо иметь:
· описание входящего потока требований,
· описание способа, каким выполняется обслуживание,
· описание дисциплины очереди, то есть указание того, каким образом требования поступают из очереди на обслуживание (варианты: живая очередь – первым пришел, первым обслужился и ушел; обслуживание с учетом приоритетов; обслуживание с отказами, когда длина очереди ограничена, и если очередь заполнена, то новые требования не принимаются).
Математическая теория систем массового обслуживания достаточно хорошо разработана, однако при исследовании реальных систем удобнее использовать специальные программные средства, позволяющие исследовать поведение систем при различных условиях.
Одной из самых известных в мире универсальных сред моделирования является система моделирования общего назначения GPSS (GENERAL PURPOSE SIMULATING SYSTEM) [7, 8]. Она предназначена для построения статистических (имитационных, на основе метода Монте-Карло) моделей дискретных сложных систем различной физической природы. Общим для систем, исследование которых может проведено с помощью GPSS, является наличие различных случайных факторов, существенным образом влияющих на смену состояний в системе. При этом предполагается, что множество состояний исследуемой системы является дискретным (конечным или счетным); смена состояний происходит в некоторые моменты времени. Интервалы между моментами смены состояний могут быть как случайными, так и детерминированными величинами. В течение всего интервала времени между моментами смены состояний исследуемая система состояния не меняет.
Существенной особенностью GPSS является ориентация на построение моделей таких систем, в которых возможно возникновение очередей различного рода. К таким системам относятся всевозможные системы массового обслуживания (СМО), вычислительные системы (ВС), транспортные - в том числе и железнодорожные - системы и т.д.
С помощью средств GPSS экспериментатор имеет возможность описать как алгоритм функционирования исследуемой системы, так и воздействие случайных факторов на систему. Таким образом, GPSS может рассматриваться и как некоторый язык описания сложных систем.
Составив описание, экспериментатор получает возможность постановки различных экспериментов, в ходе которых многократно воспроизводятся случайные ситуации, соответствующие возможным случаям воздействия внешних факторов на исследуемую систему, находящуюся в различных состояниях.
В процессе моделирования с помощью ЭВМ случайных ситуаций накапливается информация о качестве функционирования исследуемой системы в виде конкретных реализаций численных значений показателей качества функционирования. Розыгрыш случайных ситуаций продолжается до тех пор, пока объем выборки не станет достаточным для вычисления статистически достоверных оценок показателей качества функционирования.
На основании оценок качества функционирования системы, полученных в результате эксперимента с моделью, может быть проведен поиск как наилучших условий работы, так и наилучшей структуры исследуемой системы. Для решения задач оптимизации GPSS допускает стыковку с алгоритмическим языком FORTRAN-4; в этом случае программа задания начальных условий моделирования, определения направления движения в допустимой области варьирования изменяемых параметров системы пишется на языке FORTRAN, а модель системы строится на основе элементов (объектов) GPSS. Кроме того, с помощью FORTRAN-надстройки над GPSS-моделью удается существенно упростить, сделать более гибкой и саму GPSS-модель.
Следует отметить, что система GPSS была создана достаточно давно и поэтому не обладает такими эргономическими свойствами, к которым привыкли современные пользователи. В частности отсутствует возможность визуальной разработки моделей, не очень удобно представление результатов моделирования. Тем не менее, освоив эту систему, можно получить достаточно мощный инструмент моделирования. Поэтому в настоящем курсе предусмотрено выполнение лабораторных работ с использованием программы GPSS.
6.8 Сетевые модели (N – модели)
Возможности сетевых моделей мы рассмотрим на примере раскрашенных сетей Петри (Coloured Petri Nets – CPN). Особенность этой методологии состоит в том, что она моделирует системы в терминах «условия – события», что позволяет исследовать динамику работы системы. Модели на основе CPN («событийные модели») в настоящее время встраиваются в универсальные системы моделирования информационных систем таких как ARIS, IDEF и другие. Для автономного использования методологии CPN разработан специальный язык моделирования – Coloured Petri Net Modeling Language (CPN ML) и созданы соответствующие программные средства [14, 15, 17, 18].
Методология CPN близка к структурным методам моделирования систем, однако в отличие от многих из них, она базируется на хорошо разработанном математическом аппарате и поэтому допускает проведение аналитических и имитационных исследований. В настоящем пособии дается и краткое и по возможности неформализованное описание этой методологии ориентированное на синтаксис языка Паскаль. Полное и строгое описание CPN содержится в трехтомной моно-графии Курта Йенсена [18].
Как следует из названия, модель динамической системы в методологии CPN представляет собой сеть – двудольный ориентированный мультиграф. Сеть содержит узлы двух типов – позиции и переходы, связанные дугами. При этом позиции моделируют наличие в системе определенных ресурсов, необходимых для наступления события. Различные виды ресурсов условно обозначаются разными «цветами», что объясняет название методологии. Переходы моделируют сами события. Наступление какого-либо события в системе изменяет условия, что может привести к новым событиям. Дуги моделируют причинно-следственные связи в системе. Последовательность условий и событий во времени и есть модель динамики системы.
6.8.1 Мультимножества
Одним из важных понятий, используемых в теории CPN для описания ресурсов, является понятие мультимножества.
Формально мультимножеством  на непустом множестве
на непустом множестве 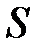 называется функция
называется функция 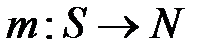 , где
, где  - множество натуральных чисел.
- множество натуральных чисел.
Иными словами, мультимножество  состоит из элементов множества
состоит из элементов множества 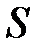 , каждый из которых может быть повторен
, каждый из которых может быть повторен 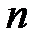 раз (
раз (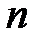 переменная целого типа). мультимножество может быть представлено в виде кортежа, в котором перечислены входящие в него элементы с указанием их кратности. Указатель кратности – выражение целого типа – ставится перед названием элемента множества и отделяется от него кавычкой. Отсутствие какого либо элемента из
переменная целого типа). мультимножество может быть представлено в виде кортежа, в котором перечислены входящие в него элементы с указанием их кратности. Указатель кратности – выражение целого типа – ставится перед названием элемента множества и отделяется от него кавычкой. Отсутствие какого либо элемента из 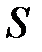 в мультимножестве эквивалентно его присутствию с нулевой кратностью. Мультимножество на
в мультимножестве эквивалентно его присутствию с нулевой кратностью. Мультимножество на 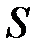 можно представить суммой
можно представить суммой
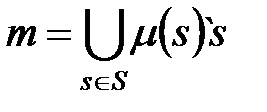
где  – число появлений (кратность) элемента
– число появлений (кратность) элемента 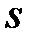 в мультимножестве
в мультимножестве  .
.
Пример: пусть 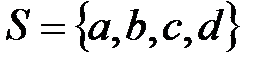 – множество элементов и
– множество элементов и 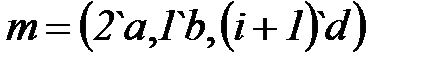 – мультимножество на
– мультимножество на  . Последняя запись означает, что
. Последняя запись означает, что  состоит из двух элементов
состоит из двух элементов  , одного элемента
, одного элемента 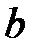 , нуля (ни одного) элементов
, нуля (ни одного) элементов 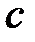 и
и  элементов
элементов 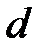 , где
, где 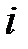 – переменная типа
– переменная типа 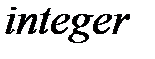 .
.
Рассмотрим операции над мультимножествами.
1. Сложение мультимножеств.
Пусть 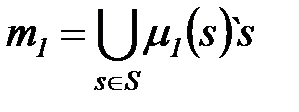 ,
, 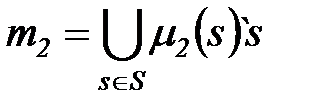 .
.
Тогда  .
.
2. Умножение мультимножества на скаляр.
Пусть 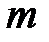 мультимножество,
мультимножество, 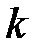 - скаляр типа
- скаляр типа 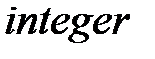 .
.
Тогда  .
.
3. Сравнение мультимножеств.
Мы будем говорить, что 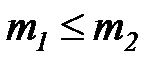 ,
,
если 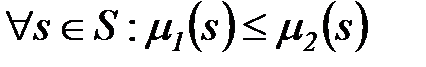 .
.
4. Вычитание мультимножеств. если 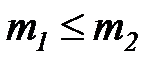 , то можно определить разность мультимножеств:
, то можно определить разность мультимножеств:
 .
.
6.8.2 Формальное определение CPN
раскрашенная сеть Петри CPN – это кортеж, состоящий из девяти элементов:
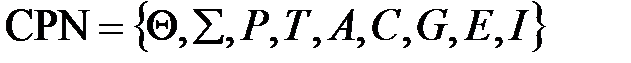 . (6.38)
. (6.38)
Рассмотрим элементы определения (6.38).
1. 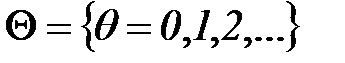 – множество дискретных моментов времени (шагов), в которые происходит функционирование сети. Номер шага есть переменная целого типа:
– множество дискретных моментов времени (шагов), в которые происходит функционирование сети. Номер шага есть переменная целого типа:
var teta: Integer;
2. 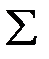 – конечное множество непустых типов, называемое цветами. Типы имеют общее название
– конечное множество непустых типов, называемое цветами. Типы имеют общее название  и задаются аналогично тому, как это принято в языках программирования. Например:
и задаются аналогично тому, как это принято в языках программирования. Например:
 ; – перечисляемый тип, здесь
; – перечисляемый тип, здесь 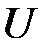 - имя цветного множества,
- имя цветного множества,  ,
, 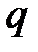 ,
, 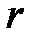 – входящие в него цвета;
– входящие в него цвета;
 ; – целый тип;
; – целый тип;  ; – прямое произведение типов.
; – прямое произведение типов.
При описании переменных, используемых в сети, указывают их принадлежность к типу, например:
 ;
;  ;
; 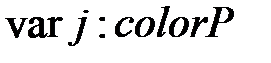 .
.
В последнем примере переменная  состоит из пары элементов
состоит из пары элементов  , где элемент
, где элемент 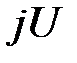 принадлежит типу
принадлежит типу 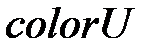 , а
, а  - типу
- типу 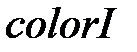 .
.
3.  – конечное множество позиций. Это множество может быть представлено перечисляемым типом:
– конечное множество позиций. Это множество может быть представлено перечисляемым типом:
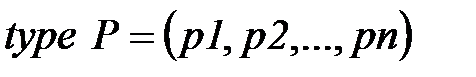 ; (6.39)
; (6.39)
а для работы с ним вводится переменная 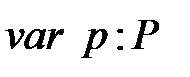 .
.
С каждой позицией может быть связана определенная маркировка, которая учитывает наличие в данной позиции различных типов ресурсов. Маркировка позиции 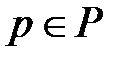 представляет собой мультимножество, например, следующего вида:
представляет собой мультимножество, например, следующего вида:
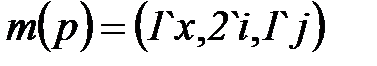 .
.
Здесь  ,
, 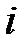 ,
,  - переменные указанных в п. 2 цветовых типов, определяющие различные виды ресурсов, а цифры, стоящие перед кавычками – количество фишек соответствующего типа, в позиции
- переменные указанных в п. 2 цветовых типов, определяющие различные виды ресурсов, а цифры, стоящие перед кавычками – количество фишек соответствующего типа, в позиции 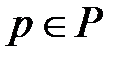 .
.
Совокупность маркировок всех позиций называется маркировкой сети:
 .
.
В языке Паскаль мультимножество, определяющее маркировку позиции, может быть представлено, например, типом – множество, состоящим из записей вида
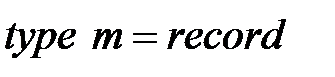 (6.40)
(6.40)
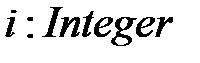 ;
; 
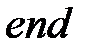 ;
;
Операции над мультимножествами можно определить соответствующими процедурами. Аналогично определяется мультимножество, задающее маркировку сети.
4. 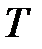 – конечное множество переходов, которое можно представить перечисляемым типом
– конечное множество переходов, которое можно представить перечисляемым типом
 ; (6.41)
; (6.41)
и соответствующей переменной:
 .
.
5. 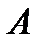 - конечное множество дуг, связывающих между собой позиции и переходы. В языке CPN ML указываются все дуги с помощью выражений вида:
- конечное множество дуг, связывающих между собой позиции и переходы. В языке CPN ML указываются все дуги с помощью выражений вида: 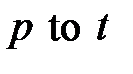 и
и  , где
, где 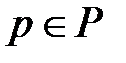 ,
, 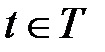 . Такая нотация введена для того, чтобы можно было пару элементов
. Такая нотация введена для того, чтобы можно было пару элементов 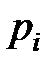 ,
,  соединить несколькими дугами с различными свойствами.
соединить несколькими дугами с различными свойствами.
В этих выражениях первый элемент указывает начало дуги, второй элемент – конец дуги.
множество 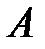 имеет структуру
имеет структуру 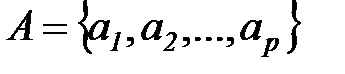 , где дуги
, где дуги 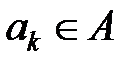 определяются одним из видов выражений:
определяются одним из видов выражений:
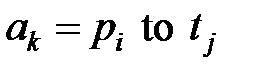 или
или 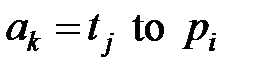 ,
, 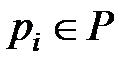 ,
, 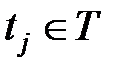 ,
,
Поскольку дуги имеют два вида: от позиции к переходу (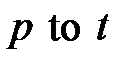 ) и от перехода к позиции (
) и от перехода к позиции (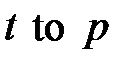 ), то множество
), то множество  можно представить в виде суммы непересекающихся множеств:
можно представить в виде суммы непересекающихся множеств: 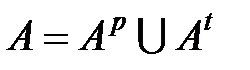 ,
, 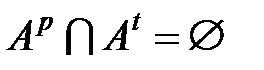 , где множество
, где множество  содержит элементы вида
содержит элементы вида 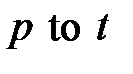 , а множество
, а множество 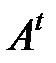 - элементы вида
- элементы вида  .
.
Элементы множеств 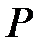 ,
,  ,
, 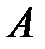 не пересекаются:
не пересекаются:
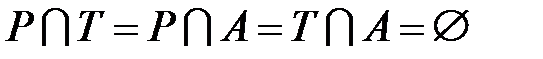 .
.
6. 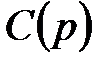 – цветовая функция, определяющая множество типов цветов, разрешенных для каждой позиции. Например, запись
– цветовая функция, определяющая множество типов цветов, разрешенных для каждой позиции. Например, запись

означает, что цвета типа 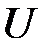 разрешены для позиций
разрешены для позиций  , а цвета типа
, а цвета типа 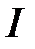 разрешены для всех остальных позиций из
разрешены для всех остальных позиций из  .
.
7. 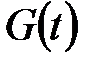 – блокировочная (спусковая) функция, описывающая дополнительные условия, которые должны быть выполнены для срабатывания перехода
– блокировочная (спусковая) функция, описывающая дополнительные условия, которые должны быть выполнены для срабатывания перехода  . Эта функция представляет собой предикат, составленный из переменных, принадлежащих типам цветов
. Эта функция представляет собой предикат, составленный из переменных, принадлежащих типам цветов  . Например, функция
. Например, функция

принимает истинное значение для перехода 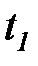 если переменная
если переменная 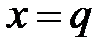 , а во всех остальных случаях она ложь. Таким образом, для того, чтобы было разрешено срабатывание перехода
, а во всех остальных случаях она ложь. Таким образом, для того, чтобы было разрешено срабатывание перехода 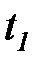 требуется выполнение дополнительного условия
требуется выполнение дополнительного условия  на входной дуге к
на входной дуге к 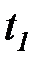 . Если эта функция не определена, то по умолчанию предполагается истинной.
. Если эта функция не определена, то по умолчанию предполагается истинной.
8. 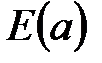 – функция, задающая выражения на дугах
– функция, задающая выражения на дугах  . Эта функция для каждой дуги
. Эта функция для каждой дуги  определяет мультимножество, состоящее из элементов, описанных в множестве цветов
определяет мультимножество, состоящее из элементов, описанных в множестве цветов 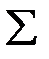 . Мы будем говорить, что это мультимножество помечает дугу. Введение в CPN функции
. Мы будем говорить, что это мультимножество помечает дугу. Введение в CPN функции 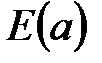 является развитием понятия кратности дуг в формализме обыкновенных СП.
является развитием понятия кратности дуг в формализме обыкновенных СП.
Рассмотрим примеры задания функции 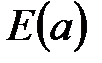 .
.
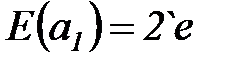 – дуга
– дуга 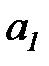 помечается двумя фишками типа
помечается двумя фишками типа  ;
;
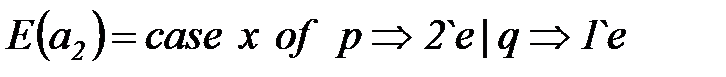 - дуга
- дуга 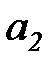 помечается двумя фишками типа
помечается двумя фишками типа 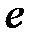 , если переменная
, если переменная 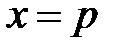 и одной фишкой типа
и одной фишкой типа  , если
, если  .
.
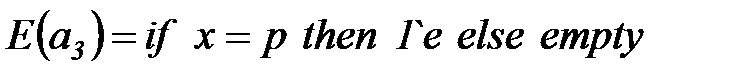 – дуга
– дуга  помечается одной фишкой типа
помечается одной фишкой типа  , если
, если  , иначе не помечается.
, иначе не помечается.
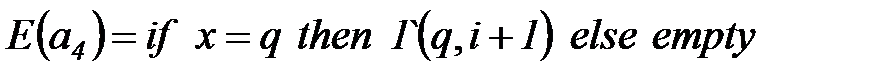 – дуга
– дуга 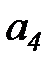 помечается одной фишкой типа
помечается одной фишкой типа  (см. пример в п. 2), если
(см. пример в п. 2), если  и не помечается в противном случае.
и не помечается в противном случае.
Отсутствие выражения для какой-либо дуги означает, что дуга не помечена.
9.  – функция инициализации сети CPN. Эта функция по аналогии с обыкновенными СП задает начальную маркировку (разметку) сети
– функция инициализации сети CPN. Эта функция по аналогии с обыкновенными СП задает начальную маркировку (разметку) сети 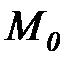 , т.е. для каждой позиции
, т.е. для каждой позиции  указывает цветовое мультимножество, обозначаемое
указывает цветовое мультимножество, обозначаемое  .
.
Например, 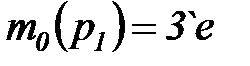 ;
; 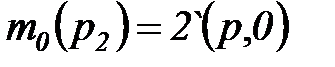 ;
; 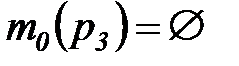 – начальные маркировки позиций, их совокупность
– начальные маркировки позиций, их совокупность  – начальная маркировка сети.
– начальная маркировка сети.
6.8.3 Функционирование CPN
Рассмотрим работу раскрашенных сетей Петри. Функционирование CPN состоит в срабатывании переходов и происходящих вследствие этого изменениях маркировок.
Мы будем говорить, что переход 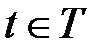 может сработать, если выполняется условие:
может сработать, если выполняется условие:
 . (6.42)
. (6.42)
В первой скобке выражения (6.36) происходит поэлементное сравнение мультимножества, являющегося маркировкой позиции 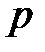 с мультимножеством, которым помечены дуги, ведущие от
с мультимножеством, которым помечены дуги, ведущие от 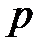 к
к  . Суммирование мультимножеств
. Суммирование мультимножеств 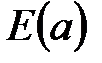 связано с тем, что, как отмечалось в п.8 определения CPN, два узла могут быть соединены несколькими дугами, и суммирование производится по всем таким дугам.
связано с тем, что, как отмечалось в п.8 определения CPN, два узла могут быть соединены несколькими дугами, и суммирование производится по всем таким дугам.
Во второй скобке записано условие отсутствия блокировки перехода  (см. п. 7 определения).
(см. п. 7 определения).
Если условие срабатывания перехода 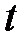 выполняется, то он может сработать, при этом говорят, что выполнится шаг работы CPN. Отсчет шагов производится в дискретном времени
выполняется, то он может сработать, при этом говорят, что выполнится шаг работы CPN. Отсчет шагов производится в дискретном времени 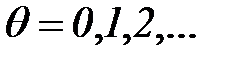 . Поэтому маркировку отдельных позиций
. Поэтому маркировку отдельных позиций 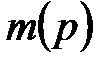 и сети в целом
и сети в целом  мы будем также привязывать ко времени и записывать соответственно в виде
мы будем также привязывать ко времени и записывать соответственно в виде 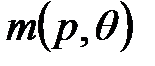 и
и 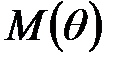 .
.
Изменение маркировки узла 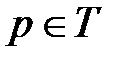 при осуществлении шага работы CPN рассчитывается по формуле:
при осуществлении шага работы CPN рассчитывается по формуле:
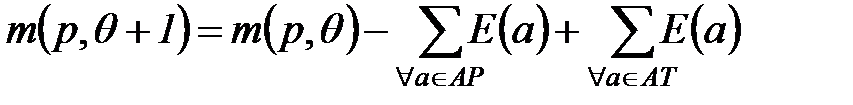 . (6.43)
. (6.43)
В выражении (6.43) все слагаемые являются мультимножествами, и вычисления производятся в соответствии с правилами сложения и вычитания мультимножеств. Знаки суммирования мультимножеств используются в формуле по причине, которая уже пояснена выше: каждая пара узлов может быть связана несколькими дугами, а каждая дуга  помечена отдельным выражением
помечена отдельным выражением 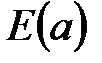 .
.
Если на некотором шаге 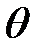 выполняются условия срабатывания нескольких переходов, то в зависимости от задачи исследования CPN мы можем разрешить сработать всем переходам (при построении дерева всех возможных маркировок), либо дать такую возможность только одному из них на основе некоторых дополнительных условий (например, приоритетов).
выполняются условия срабатывания нескольких переходов, то в зависимости от задачи исследования CPN мы можем разрешить сработать всем переходам (при построении дерева всех возможных маркировок), либо дать такую возможность только одному из них на основе некоторых дополнительных условий (например, приоритетов).
Формальное определение сети Петри, приведенное выше, полностью определяет ее функционирование. Однако при решении конкретных задач моделирования часто удобнее и нагляднее использовать графическое представление этих сетей.
Теоретико-графовым представлением сети Петри является двудольный ориентированный мультиграф сети Петри.
Этот граф в соответствии с приведенным выше определением содержит:
- позиции (места), обозначаемые кружками, маркировка которых моделирует наличие определенных условий в системе;
- переходы, обозначаемые планками, срабатывания которых моделируют события в системе;
- ориентированные дуги (стрелки), соединяющие позиции с переходами и переходы с позициями.
Кроме того, в дополнение к формальному описанию CPN на графе для наглядности могут быть указаны следующие элементы:
- маркировка, условно обозначаемая количеством ресурсов (фишек) внутри позиций;
- выражения на дугах;
- выражения для блокировочных функций на переходах.
6.8.4 CPN с временным механизмом
Существует ряд задач моделирования, в которых необходимо учитывать не только последовательность событий, но и время их наступления, а также продолжительность. Для этой цели предусмотрено расширение возможностей раскрашенных сетей Петри путем введения временного механизма (так называемых timed CPN [18]). В несколько упрощенном виде сущность такого расширения описана ниже.
А. В модель системы вводятся часы, показывающие глобальное время  . Обычно это время считается дискретным, т.е. означает номер такта, выдаваемого тактовым генератором системы моделирования. Глобальное время
. Обычно это время считается дискретным, т.е. означает номер такта, выдаваемого тактовым генератором системы моделирования. Глобальное время  отличается от времени
отличается от времени  , которое содержится в определении (6.49), поскольку
, которое содержится в определении (6.49), поскольку 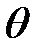 есть номер шага работы CPN, а
есть номер шага работы CPN, а  изменяется независимо от работы сети.
изменяется независимо от работы сети.
Б. Ресурсы, перемещаемые в сети (фишки) могут получить временные метки. Такие ресурсы в общем виде задаются мультимножествами с временными метками (timed multi-sets), однако мы эту теорию не рассматриваем. Отметим лишь, что при описании множества цветов добавляются пометки timed, а переменные соответствующего типа снабжаются знаками @ (по-английски читается at, т.е. «во время»). Это означает, что переменная привязана к глобальному времени. После значка @ в квадратных скобках указывается значение глобального времени, в течение которого возможно использование данных фишек для срабатывания переходов, для которых они являются входными. При этом запись вида @[500] говорит о том, что фишка «включается» в момент 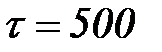 и далее готова для работы в сети, а запись @[500, 600] означает, что фишка может использоваться в диапазоне глобального времени
и далее готова для работы в сети, а запись @[500, 600] означает, что фишка может использоваться в диапазоне глобального времени 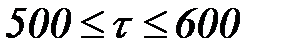 .
.
Приведем пример:
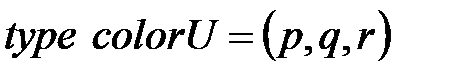 ;
;
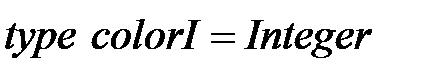 ;
;
 ;
;
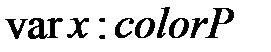 .
.
Возможное значение мультимножества определяемого переменной x:
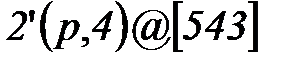 . Приведенная запись означает, что переменная x содержит 2 фишки (мультимножества), каждая которых содержит два ресурса: цвета p из цветового множества colorU и целочисленный ресурс, равный 4. Эта переменная «включается» в момент
. Приведенная запись означает, что переменная x содержит 2 фишки (мультимножества), каждая которых содержит два ресурса: цвета p из цветового множества colorU и целочисленный ресурс, равный 4. Эта переменная «включается» в момент 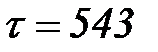 .
.
В. Каждый переход, на вход которого поступают фишки, имеющие временные метки, получает дополнительное условие срабатывания: он может сработать только в том случае, если системное время удовлетворяет всем условиям на входных фишках.
В свою очередь, при срабатывании переход может увеличить временную метку фишки, т.е. смоделировать задержку в работе системы. Величина задержки определяется специальным выражением, связанным с переходом, и имеющим вид  , где
, где  - время задержки, задаваемое числом или функцией.
- время задержки, задаваемое числом или функцией.
Пусть в сети на рисунке 6.9 начальная маркировка такова: 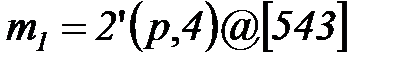 ,
,  . Выражения на дугах показаны на схеме. Глобальное время
. Выражения на дугах показаны на схеме. Глобальное время 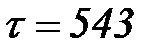 . Переход
. Переход 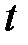 может сработать, при этом он осуществит задержку передачи фишек в
может сработать, при этом он осуществит задержку передачи фишек в 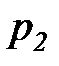 на 12 единиц времени в соответствии с выражением на
на 12 единиц времени в соответствии с выражением на 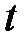 . Таким образом, после срабатывания
. Таким образом, после срабатывания 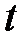 получим маркировку:
получим маркировку: 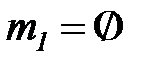 ,
,  .
.
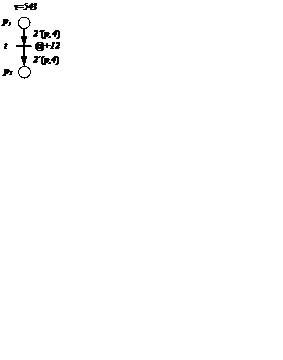
Рисунок 6.9 Сеть Петри с временными метками.
6.8.5 Пример модели информационного процесса
Проиллюстрируем возможности рассмотренной теории на примере модели процесса обучения. Рассмотрим процесс прохождения под управлением автоматизированной обучающей системы интерактивного одного модуля учебного курса. Процесс прохождения учащимся учебного модуля заключается в следующем. Из базы учебных модулей извлекается очередная порция теоретического материала, которую предлагается освоить обучаемому. После того, как обучаемый окончил изучения этого материала, система приступает к тестированию. Из базы тестов выбирается тестовый материал и предъявляется обучаемому, который готовит и вводит в систему ответы на тестовые задания. Эти ответы анализируются системой оценивания, которая принимает решение:
· ответы верные, в этом случае изучение данного модуля завершается, и возможен переход к следующему модулю;
· ответы неточные, в этом случае обучаемый должен изучить дополнительный материал и затем пройти повторное тестирование;
· ответы абсурдные, в этом случае обучаемый должен изучить материал модуля с самого начала.
Модель этого процесса в виде сети Петри представлена на рисунке 6.10. Эта сеть, в соответствии с приведенным выше описанием, содержит два множества узлов: множество позиций 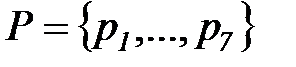 (обозначены кружками) и множество переходов
(обозначены кружками) и множество переходов 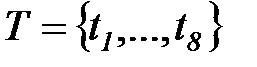 (обозначены планками). Узлы соединены дугами двух видов: от позиций к переходам и от переходов к позициям.
(обозначены планками). Узлы соединены дугами двух видов: от позиций к переходам и от переходов к позициям.
Маркировка позиций моделирует выполнение условий, а переходы при своем срабатывании – наступление событий.

Рисунок 6.10. Сеть Петри, моделирующая изучение отдельного модуля
Для простоты изложения ограничимся только одним видом ресурсов целочисленного типа, которому соответствует единственное цветовое множество:
Color INT=intrger и соответствующей переменной var s: INT.
Смысл введенного ресурса следующий: если в позиции pi имеется хотя бы одна фишка (т.е. маркировка 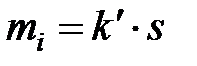 ,
,  ), то срабатывание выходного перехода возможно. Описанная сеть называется обыкновенной сетью Петри, с изучения таких сетей началась разработка рассматриваемой теории.
), то срабатывание выходного перехода возможно. Описанная сеть называется обыкновенной сетью Петри, с изучения таких сетей началась разработка рассматриваемой теории.
В этом случае выражения на всех дугах имеют один и тот же вид:  , что означает передачу по дуге единичного целочисленного ресурса. Поэтому на рисунке выражения на дугах не показаны.
, что означает передачу по дуге единичного целочисленного ресурса. Поэтому на рисунке выражения на дугах не показаны.
Рассмотрим смысл условий и событий, происходящих в системе.
Условия, моделируемые позициями:
p1 - изучение модуля возможно,
p2 - основной материал модуля выбран,
p3 - выбор теста возможен,
p4 - тест выбран,
p5 - оценивание ответа произведено,
p6 - дополнительный материал модуля выбран,
p7 - переход к следующему модулю возможен,
pM - база основных учебных модулей,
pD - база дополнительных материалов,
pT - база тестовых материалов,
pJ – журнал учета пройденных модулей.
События, моделируемые переходами:
t1 - изучение основного материала модуля начинается,
t2 - изучение основного материала модуля завершается,
t3 - тестирование начинается,
t4 - тестирование завершается,
t5 - изучение дополнительного материала начинается,
t6 - изучение дополнительного материала завершается,
t7 - повторное изучение модуля начинается,
t8 - изучение модуля завершается.
Начальная маркировка позиций, как показано на рисунке, выглядит следующим образом:
 ,
, 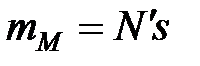 ,
, 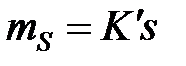 ,
, 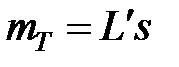 . (6.44)
. (6.44)
Здесь M - количество модулей в курсе, N - количество дополнительных разделов, L - количество тестов. Предполагается, что M< N< < L.
Все остальные позиции в начальный момент не содержат ресурсов, т.е. имеют нулевую маркировку.
Поясним работу сети. В соответствии с правилами функционирования сети Петри (п. 6.8.3) на первом шаге может сработать переход t1 (что соответствует событию: изучение основного материала модуля начинается). При этом будет изъято по одной фишке из позиций pM и p1 , и одна фишка будет помещена в позицию p2. Выполнится соответствующее условие, и появится возможность сработать переходу t2. Описанный процесс продолжится, аналогичным образом сработают переходы t2, t3 и t4. После выполнения условия p5 - оценивание ответа произведено, возможно разветвление процесса по трем направлениям, т.е. может произойти одно из трех описанных выше событий, которые моделируются переходами t5, t7, t8. При срабатывании перехода t8 и попадании фишки 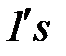 в позицию p7 моделируемый процесс завершается. Кроме того, помещается фишка
в позицию p7 моделируемый процесс завершается. Кроме того, помещается фишка  в позицию
в позицию  , что соответствует фиксации этого факта в журнале учета АОС.
, что соответствует фиксации этого факта в журнале учета АОС.
6.8.6 Вложенные сети Петри
Рассмотрим еще одно расширение сетей Петри, которое может оказаться полезным при моделировании процессов, в которых происходит взаимодействие отдельных подсистем с системой и между собой. Речь идет о так называемых вложенных сетях Петри (Nested Petri Nets – NPN) [19].
Появление указанной разновидности сетей Петри связано с желанием исследователей иметь инструмент для адекватного и удобного представления систем со сложной иерархической и мультиагентной структурой.
Вложенные сети Петри представляют собой расширение стандартного формализма сетей Петри, в котором фишки, представляющие локальные ресурсы в позициях системной сети, сами могут быть сложными объектами с сетевой структурой и моделироваться сетями Петри нижнего уровня – их мы также будем называть сателитными сетями.
Структурно такая сеть состоит из системной сети SN и набором сетей-фишек (сателлитов) ENi, i=1,..., n. При этом между некоторыми переходами системной сети и переходами сетей-фишек может быть установлена связь, разрешающая только их совместное срабатывание. Такие переходы называются помеченными.
Функционирование сетей, входящих в NPN, в значительной мере совпадает с функционированием ранее рассмотренных сетей Петри. Отличие составляют механизмы синхронизации работы сетей Петри различного уровня. В связи с этим в NPN различают следующие четыре вида шагов срабатывания.
Системно-автономный шаг, который соответствует срабатывнию непомеченного перехода в системной сети SN.
Сателитно-автономный шаг, который соответствует срабатыванию непомеченного перехода в сети-фишке ENi..
Шаг горизонтальной синхронизации, при котором одновременно срабатывают переходы в сетях-фишках ENi, помеченные одинаковыми метками.
Шаг вертикальной синхронизации, при котором одновременно срабатывают переходы в системной сети SN и сетях-фишках ENi, имеющие одинаковые метки.
Разумеется, при этом предполагается, что во всех сетях все участвующие в работе переходы являются активными, т.е. в их входных позициях имеются необходимые для срабатывания ресурсы.
Проиллюстрируем возможности вложенных сетей Петри для получения модели процесса обучения. В предыдущем разделе была рассмотрена модель процесса интерактивного обучения, показанная на рисунке 6.8. В этой модели каждый обучаемый моделировался одной фишкой, обозначаемой переменной var s: STUDENT, которая соответствует целочисленному коду обучаемого. При этом информация об истории прохождении курса конкретным студениом теряется после того, как процесс обучения завершен. Кроме того, в модели на рисунке 6.8 не прослеживается процесс обучения в динамике, отсутсвует возможность дифференцированного оценивания успешности обучения. Также не предусмотрена возможность неудачного завершения курса, поскольку число попыток изучения материала и тестирования не ограничено
Функциональность системы можно повысить, если моделировать поведение каждого обучаемого с помощью отдельной сети Петри. Тогда фишка, обозначаемая переменной s, станет сетью ENs, где s – код обучаемого, как принято в п. 6.8.5.
При этом получится вложенная сеть Петри, которая состоит из системной сети SN (она изображена на рисунке 6.10) и набора сателлитных сетей ENs (s=1, 2, …). Один из возможных вариантов сети ENs представлен на рисунке 6.11.
Кратко поясним работу вложенной сети. На рисунке 6.9 позиции обозначены буквами qi, i = 1, …, 10. Смысл позиций q1, …, q6 совпадает со смыслом позиций p11, …, p16 на рисунке 6.8, остальные позиции относятся к оценке успешности обучения. Переходы t1, t11, …, t17 на обоих рисунках имеют один и тот же смысл. При этом черта над обозначением перехода на рисунке 6.9 означает наличие вертикальной синхронизации: одноименные переходы могут сработать только одновременно. Это означает синхронизацию следующих действий:
· приход обучаемого в систему (срабатывание перехода t1), создание в системной сети SN сателлитной сети ENs в виде фишки s; в свою очередь, в сателлитной сети переменная s относится к цветовому множеству STUDENT;
· выбор учебного модуля и начало процесса обучения – срабатывание переходов t11;
· завершение процесса обучения и выбор тестов – срабатывание переходов t13;
· завершение процесса тестирования и переход к оцениванию – срабатывание переходов t14;
· принятие решения по результатам тестирования – срабатывание переходов: t15 - изучение дополнительного материала, t16 - завершение изучения модуля, t17 – повторное изучение всего материала.
Кроме описанных событий сеть ENs позволяет оценить количество баллов, набранных учащимся в процессе изучения модуля. Для этого введены дополнительные ресурсы, задаваемые цветовыми множествами:
Color BALL = integer,
Color FAILURE = boolean
и соответствующие переменные:
var β: BALL, var γ: FAILURE.
Переменная  означает количество баллов, набранных учащимся при выполнении модуля. Первоначально в позиции q9 находится 100 баллов, а затем при каждой неудаче маркировка этой позиции уменьшается: при необходимости изучения дополнительного материала – на b1 баллов, а при необходимости повторного изучения всего курса – на b2 баллов. При успешном завершении процесса обучения срабатывает переход t5, и в позицию q10 передается набранное учащимся количество баллов – число b.
означает количество баллов, набранных учащимся при выполнении модуля. Первоначально в позиции q9 находится 100 баллов, а затем при каждой неудаче маркировка этой позиции уменьшается: при необходимости изучения дополнительного материала – на b1 баллов, а при необходимости повторного изучения всего курса – на b2 баллов. При успешном завершении процесса обучения срабатывает переход t5, и в позицию q10 передается набранное учащимся количество баллов – число b.
Минимальное число баллов, при котором возможна положительная оценка, составляет b0 баллов. Если текущее значение величины  окажется меньше b0, то процесс обучения признается неудачным, и переменная
окажется меньше b0, то процесс обучения признается неудачным, и переменная 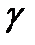 принимает значение true, которое передается в позицию q10 при срабатывании перехода t5. Все остальные переходы при этом оказываются заблокированными.
принимает значение true, которое передается в позицию q10 при срабатывании перехода t5. Все остальные переходы при этом оказываются заблокированными.
В рассмотренном примере использована только вертикальная синхронизация, которая заключается в требовании одновременного срабатывания переходов в сетях SN и Es. Возможно предусмотреть и горизонтальную синхронизацию между сетями Es, что позволило бы моделировать совместную работу учащихся, например, при выполнении коллективного проекта. Однако в данном примере мы такой вариант модели не рассматриваем.
if b< b0 then 1` g else empty
1`s
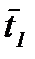
1`s
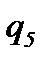
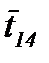
1`s
1`s

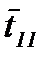
1`s
1`s


1`s
1`s


1`s
1`s
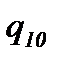
1`s
1`s; b`b
t5
q9
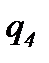
1`s
1`s
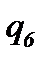

1`s
1`s
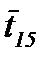
1`s
1`s
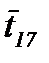
1`s
1`s

1`s
1`s
t3
t2
t4
q0
q1
if b³ b0 then (b-b2)`b else empty
if b³ b0 then b`b else empty
m0=100`b
m0=1`s
if b³ b0 then (b-b1)`b else empty
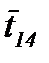
1` g
Рисунок 6.11. Вложенная сеть Es
|
|