Невырожденные матрицы

Основные понятия

Пусть А- квадратная матрица п-го порядка

Квадратная матрица А называется невырожденной, если определитель . В противном случае матрица А называется вырожденной.

Матрица называется обратной матрице А, если выполняется условие

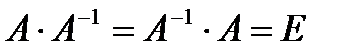
где Е- единичная матрица того же порядка, что и матрица А. Матрица имеет те же размеры, что и матрица А.

Обратная матрица

Всякая невырожденная матрица имеет обратную.

,

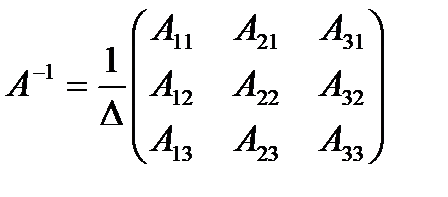
Пример 3.1. Найти

Найдем алгебраические дополнения

, , , , ,

, , ,

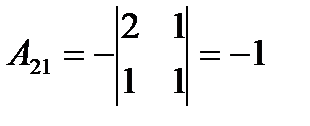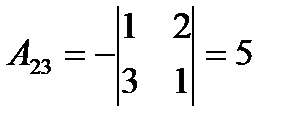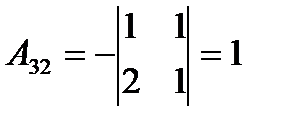Проверка: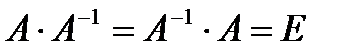

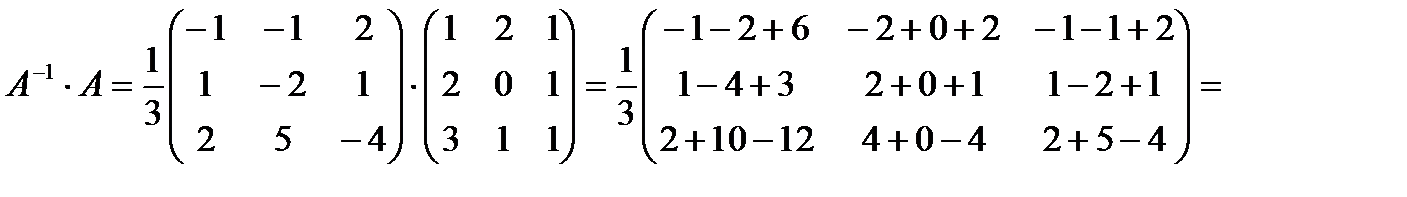
Лекция 2

Системы линейных уравнений

Основные понятия

Система линейных алгебраических уравнений, содержащей т уравнений и п неизвестных, называется система вида

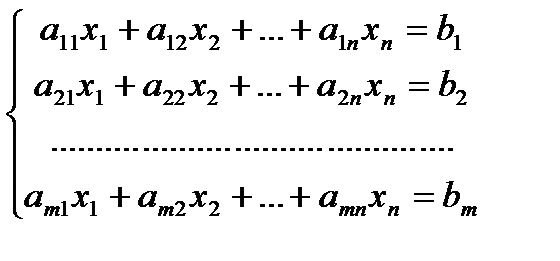
где числа 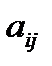, называются коэффициентами системы, числа 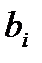- свободными членами. Подлежат нахождению числа .

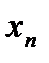Такую систему удобно записывать в матричной форме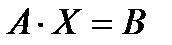

Здесь А – матрица коэффициентов системы, называемая основной матрицей:

- вектор – столбец из неизвестных 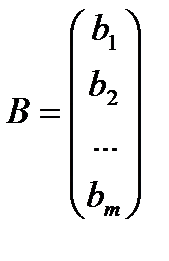- вектор – столбец из свободных членов

Произведение матриц 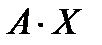определенно, так как в матрице А столбцов столько же строк в матрице Х (п штук).

Расширенной матрицей системы называется матрица 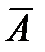системы, дополненная столбцом свободных членов

Решением системы называется п значений неизвестных при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы – столбца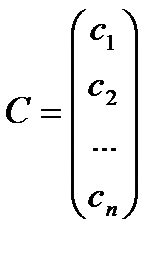

Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она имеет ни одного решения.

Решить систему – это значить выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.