Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Несобственные интегралы 1го рода
|
|

Геометрический смысл несобственного интеграла I рода: Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.
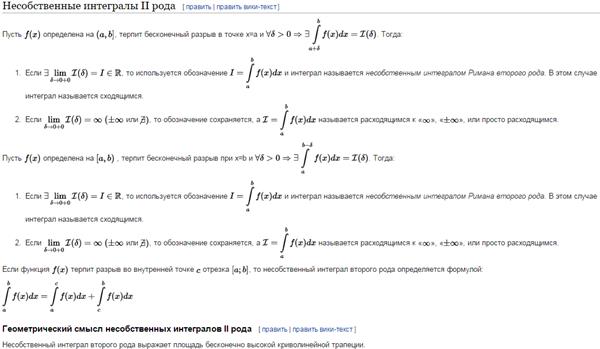

18. Применение интегралов при вычислении площади фигур. Пусть границами криволинейной трапеции являются прямые x=a, x=b, ось абсцисс и параметрически заданная кривая 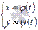 , причем функции
, причем функции 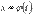 и
и 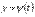 непрерывны на интервале
непрерывны на интервале 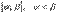 ,
, 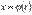 монотонно возрастает на нем и
монотонно возрастает на нем и  .
.
Тогда площадь криволинейной трапеции находится по формуле  . Эта формула получается из формулы площади криволинейной трапеции
. Эта формула получается из формулы площади криволинейной трапеции 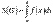 подстановкой
подстановкой 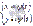 :
:
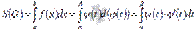
Если функция 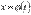 является монотонно убывающей на интервале
является монотонно убывающей на интервале 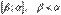 , то формула примет вид
, то формула примет вид 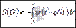 .
.
Если функция 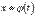 не является основной элементарной, то для выяснения ее возрастания или убывания может потребоваться теория из раздела возрастание и убывание функции на интервале.
не является основной элементарной, то для выяснения ее возрастания или убывания может потребоваться теория из раздела возрастание и убывание функции на интервале.
Параметрическое представление эллипса с центром в начале координат и полуосями a и b имеет вид 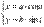 . Если действовать так же, как и в разобранном примере, то получим формулу длявычисления площади эллипса
. Если действовать так же, как и в разобранном примере, то получим формулу длявычисления площади эллипса  .
.
Окружность с центром в начале координат радиуса R через параметр t задается системой уравнений 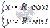 . Если воспользоваться полученной формулой площади эллипса, то сразу можно записать формулу для нахождения площади круга радиуса R:
. Если воспользоваться полученной формулой площади эллипса, то сразу можно записать формулу для нахождения площади круга радиуса R: 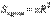 .
.
Аналогично можно показать, что площадь астроиды  находится как
находится как 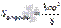 , а площадь фигуры, ограниченной линией
, а площадь фигуры, ограниченной линией 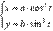 , вычисляется по формуле
, вычисляется по формуле 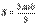 .
.

Матрицы. Основные понятия. Действия над матрицами.
Матрица — математический объект, представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задает размер матрицы. Хотя исторически рассматривались, например, треугольные матрицы, в настоящее время говорят исключительно о матрицах прямоугольной формы, так как они являются наиболее удобными и общими. Для матрицы определены следующие алгебраические операции:
* сложение матриц, имеющих один и тот же размер;
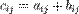
{\displaystyle \ c_{ij}=a_{ij}+b_{ij}}* умножение матриц подходящего размера (матрицу, имеющую n столбцов, можно умножить справа на матрицу, имеющую n строк);
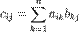
* в том числе умножение на матрицу вектора (по обычному правилу матричного умножения; вектор является в этом смысле частным случаем матрицы);
* умножение матрицы на элемент основного кольца или поля (то есть скаляр).
20.Определители: основные понятия. Свойства определителей. Вычисление определителей.
Определи́ тель (или детермина́ нт) — одно из основных понятий линейной алгебры. Определитель квадратной матрицы A размеров n x n, заданной над коммутативным кольцом R, является элементом кольца R, вычисляемым двумя способами:
Через аксиоматическое построение (определение на основе свойств).
Понятие определителя может быть введено на основе его свойств. А именно, определителем вещественной матрицы называется функция det: Rn x n => R, где
det(A) – кососимметрическая функция строк (столбцов) матрицы А.
det(A) –косолинейная функция строк (столбцов) матрицы А.
det(E) = 1, где E – единичная n x n-матрица
Через перестановки. Для матрицы n x n вычисляется 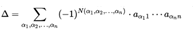
Где a1, a2,.., an – перестановка чисел от 1 до n
N(a1, a2,..., an) – число инверсий в перестановке, суммирование проводится по всем перестановкам порядка n. Таким образом, в определитель входит n! слагаемых, которые также называют «членами определителя».
Найти определитель матрицы A
| A = |
|
| det(A) = |
| = 5·1 - 7·(-4) = 5 + 28 = 33 |
| ∆ = |
| = |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 - a13·a22·a31 - a11·a23·a32 - a12·a21·a33
21. Невырожденные матрицы: основные понятия. Ранг матрицы.
Невырожденная матрица (иначе неособенная матрица) ― квадратная матрица, определитель которой отличен от нуля. В противном случае матрица называется вырожденной. Для квадратной матрицы M над полем невырожденность эквивалентна каждому из следующих условий:
M обратима, то есть существует обратная матрица;
строки (столбцы) матрицы M линейно независимы;
ранг матрицы равен её размерности.
Ранг матрицы — наивысший из порядков миноров этой матрицы, определитель которых отличен от нуля. Ранг матрицы — Размерность образа линейного оператора, которому соответствует матрица.
Рангом матрицы  называется ранг её системы строк или столбцов.
называется ранг её системы строк или столбцов.
Обозначается 
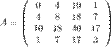 На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.
На практике для нахождения ранга матрицы используют следующее утверждение: ранг матрицы равен количеству ненулевых строк после приведения матрицы к ступенчатому виду.
Задание. Найти ранг матрицы. Решение. С помощью элементарных преобразований над ее строками приведем матрицу  к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
к ступенчатому виду. Для этого вначале от третьей строки отнимем две вторых:
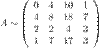 От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых:
От второй строки отнимаем четвертую строку, умноженную на 4; от третьей - две четвертых: 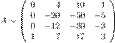
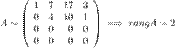 Ко второй строке прибавим пять первых, к третьей - три третьих:
Ко второй строке прибавим пять первых, к третьей - три третьих: 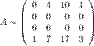 Меняем местами первую и вторую строчки:
Меняем местами первую и вторую строчки:
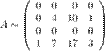 Далее четвертую и первую строки:
Далее четвертую и первую строки:
|
|