Оптимизация режимов механической обработки для дискретных значений параметров v и s

Особенностью оптимизации режимов резания для большинства видов обработки на металлорежущих станках является необходи­мость определения дискретных значений параметров v и s, которые могут принимать конкретные значения из диапазона, определяемого кинематикой станка. Для построения математической модели про­цесса резания в этом случае используются ранее установленные зависимости для технических ограничений (10.3)–(10.4), (10.12), (10.14), (10.15). Однако, учитывая, что оценочные функции для частных критериев – максимальной производительности из формулы (8.9), минимальной себестоимости из (8.13) и компромиссного критерия

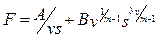, (10.21)

где 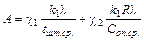; ; 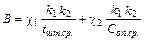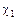, 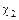- весовые коэффициенты, устанавливаемые на основе экспертных оценок; 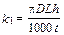; ; 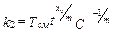представляются в виде выражения F=F(v, s), все технические ограничения должны выражаться также через значения скорости резания v и подачу s.

Исключая технические ограничения по кинематике станка, можно получить следующие выражения:

1) ограничения по стойкости режущего инструмента

;

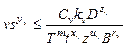2) ограничения по мощности электродвигателя главного дви­жения станка

;

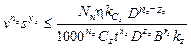3) ограничения по заданной производительности станка

;

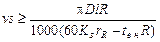4) ограничения по прочности режущего инструмента

;

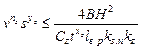5) ограничения по жесткости режущего инструмента

;

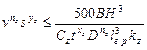6) ограничения по жесткости заготовки

;

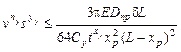7) ограничения по прочности механизма станка

;

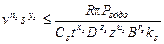8) ограничения по требуемой шероховатости поверхности

.

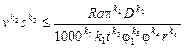Обозначим правые части неравенства соответственно , , …, .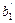

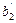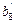В качестве компромиссной целевой функции принимаем

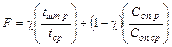(10.22)

где 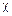– весовой коэффициент, определяющий долю влияния в функ­ции F критерия оптимальности t_шт.р и изменяющийся от 0 до 1;

; ;

; ;

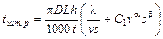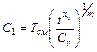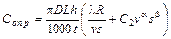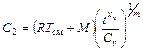t_cp, C_on.cp – средние арифметические значения t_шт, C_on на множестве значений пар (v_i, s_j).

Нетрудно заметить, что компромиссная целевая функция (10.22) в зависимости от коэффициента 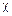может быть приведена к частному критерию оптимальности. Так, при значении 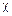=0 она преобразуется в критерий «минимальная себестоимость», а при 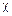=1 – критерий «максимальная производительность».

Из приведенного выше анализа поведения компромиссной целе­вой функции F в области технических ограничений видно, что алго­ритм определения оптимальных значений v и s должен обеспечить нахождение точки касания целевой функции с одним из ограниче­ний или точкой пересечения ограничения. Это достигается перебо­ром значений v_i и s_j.

Перебор производится для значений v₁, v₂,..., v_I. Для каждого v_i перебором дискретных значений s_j, начиная с наибольшего s_l (что сокращает число точек перебора, так как оптимальные значения s лежат, как правило, в правой области технических ограничений), ищется максимальное s_ji, удовлетворяющее ограничению

s_ji £ M,

где .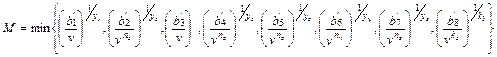

В полученной точке дискретных значений скорости (числа оборотов) и подачи вычисляется оценочная функция F(v_i, s_ji). Далее выби­рается минимум из значений F(v_i, s_ji), для 1£ i£ I. Вышеописанный алгоритм представлен на рис. 10.3.

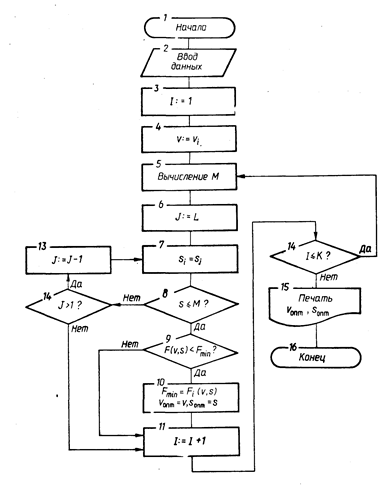
Рис.10.3. Схема алгоритма оптимизации режимов механической обработки для дискретных значений параметров v и s