Тема 3. Линейные операторы. Квадратичные формы.

Задача 7. Дана матрица линейного оператора в : .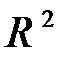

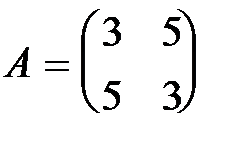1) Найти собственные значения и собственные векторы линейного оператора (матрицы).

2) Привести квадратичную форму, заданную матрицей 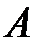в 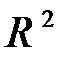, к каноническому виду, а также найти ортонормированный базис, в котором она имеет этот вид.

3).Определить, является ли квадратичная форма знакоопределенной.

4) Построить линии уровня квадратичной формы.

Решение.

1) Определение. Пусть в 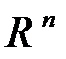задан линейный оператор (матрица) 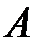, вектор 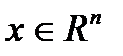, , 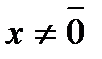удовлетворяющий условию 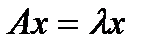(1), где 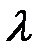- некоторое число, называется собственным вектором линейного оператора, а 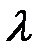- собственным значением (или числом) линейного оператора.

Если 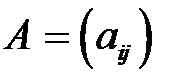- матрица линейного оператора в некотором базисе, а координаты собственного вектора 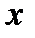в этом базисе 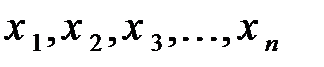, то записывая соотношением (1) в координатной форме, получим:

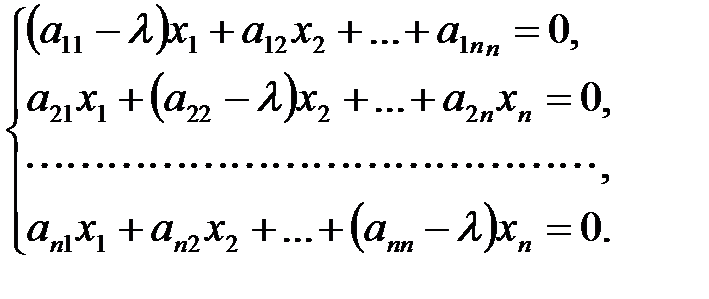(2)

Для отыскания собственного вектора, необходимо найти ненулевые решения этой однородной системы уравнений, которые существуют тогда и только тогда, когда

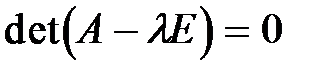. (3)

Уравнение (3) называется характеристическим уравнением, его корни являются собственными значениями линейного оператора (матрицы) 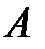. Подставляя это число в (2), найдем ненулевое решение этой системы, которое определяет искомый собственный вектор.

Составим характеристическое уравнение (3) для заданной матрицы :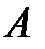

.

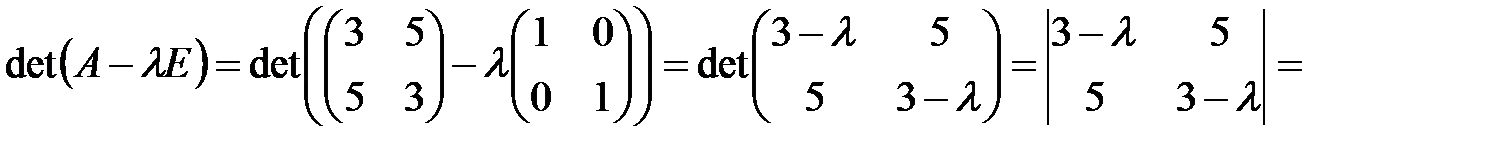
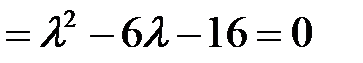Отсюда корни 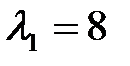, 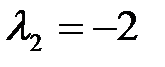– собственные значения линейного оператора.

Найдем собственные векторы, соответствующие числу 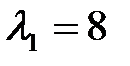. При 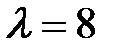система (2) имеет вид:

.

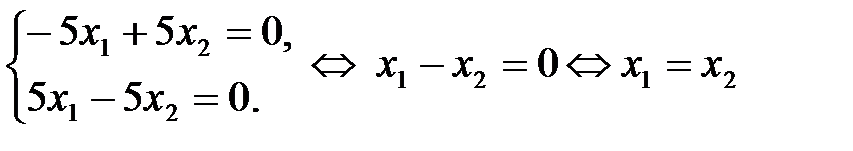Общее решение этой системы 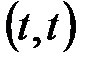, где 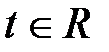, т.е. собственные векторы, соответствующие собственному числу 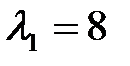имеют вид:

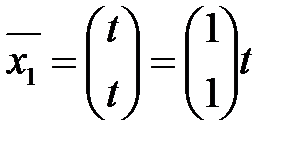, где , .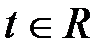

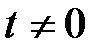Например, при 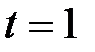один из них: .

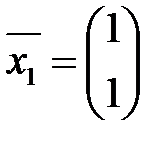Аналогично найдем собственные векторы, соответствующие числу 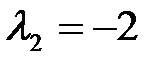. Система (2) при 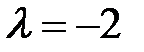имеет вид:

.

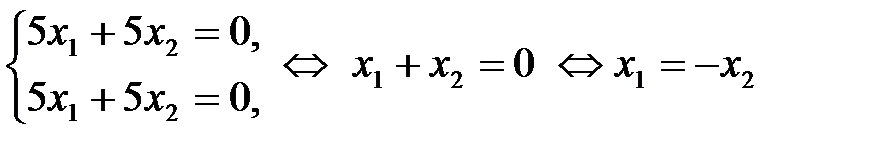Общее решени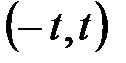е , где 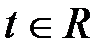. Отсюда собственные векторы, соответствующие собственному числу 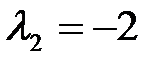имеют вид:

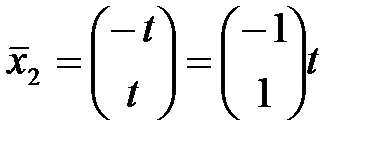, где , .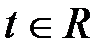

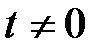Например, .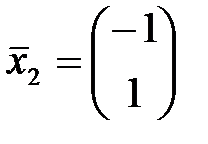

2) Определение. Рассмотрим в 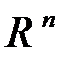произвольную симметричную матрицу (линейный оператор) , пусть 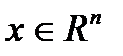- произвольный вектор. Квадратичной формой от n переменных называется скалярная функция вида:

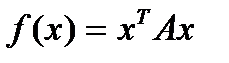. (4)

В пространстве 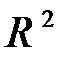она имеет вид:

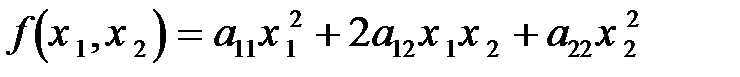, (5)

где .

Теорема. Пусть 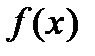– квадратичная форма в евклидовом пространстве 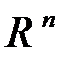и 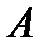– самосопряженный оператор, соответствующий этой форме. Тогда в 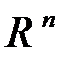существует ортонормированный базис 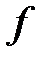, в котором 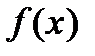приводится к каноническому виду:

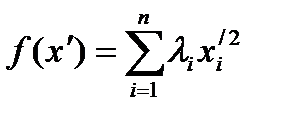, (6)

где 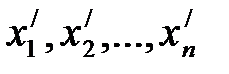– координаты вектора 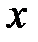в базисе 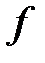, этот базис можно взять из нормированных собственных векторов оператора 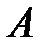с учетом кратности.

Из доказательства этой теоремы следует, что элементами этой диагональной матрицы будут собственные значения матрицы A:

. (7)

В 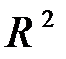канонический вид квадратичной формы (5):

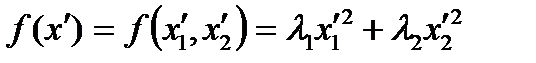, (8)

где - координаты вектора 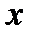в указанном ортонормированном базисе .

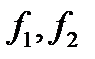Для заданной матрицы A квадратичная форма имеет вид:

.

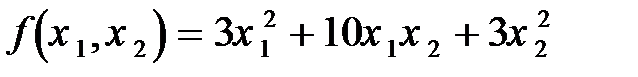Учитывая решение в пункте 1 (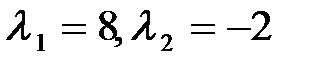) в силу указанной теоремы в новом базисе 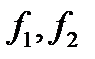квадратичная форма примет вид:

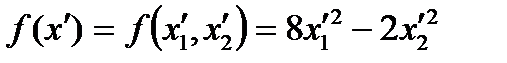- канонический вид.

Найдем ортонормированный базис, в котором она имеет этот вид. В пункте 1 мы нашли, что в качестве собственных векторов можно взять

, .

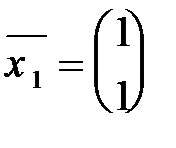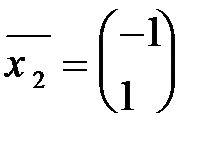Пронормируем их, для этого найдем:

.

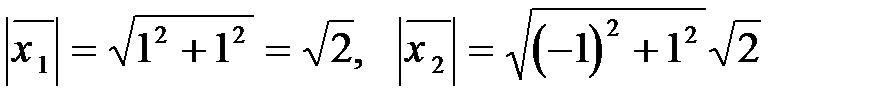Тогд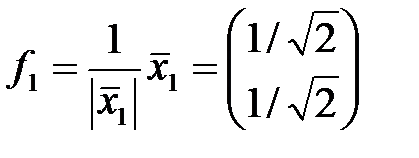а

, а .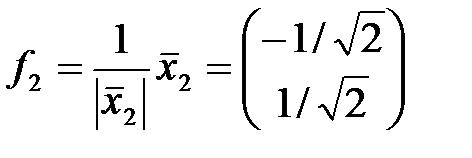

Легко убедиться, что 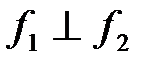, т.к. 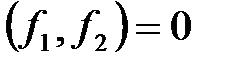и 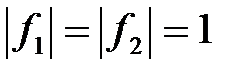. Построим векторы:

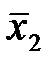
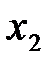
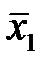
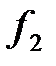
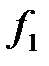
^{-1 0 1}

3) Определение. Квадратичная форма называется положительно определенной, если

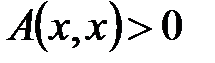
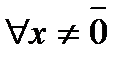(9)

и отрицательно определенной, если

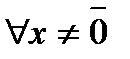. (10)

Положительные и отрицательные формы иногда называют знакопостоянными.

Теорема. Квадратичная форма положительно (отрицательно) определена, если и только если положительны (отрицательны) все соответствующие собственные значения соответствующего форме оператора.

Итак, положительная (отрицательная) определенность формы в общем случае легко устанавливается путем ее приведения к диагональному виду. Однако в отдельных случаях имеет большой интерес и непосредственный признак знакопостоянства формы. Из них мы рассмотрим так называемый критерий Сильвестра.

Критерий Сильвестра. Пусть 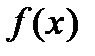– квадратичная форма в евклидовом пространстве 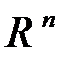и 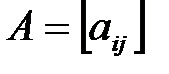– матрица соответствующего оператора в некотором базисе. Тогда:

а) 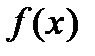положительно определена, если и только если все угловые миноры матрицы 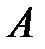положительны, т.е.

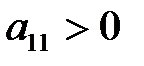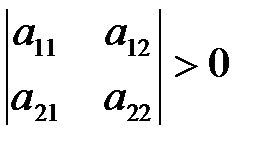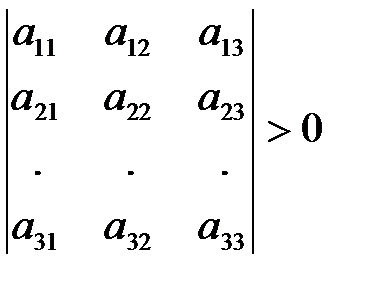, , , и т.д.

б) 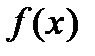отрицательно определена, если и только если знаки угловых миноров чередуются, начиная со знака минус, т.е.

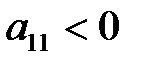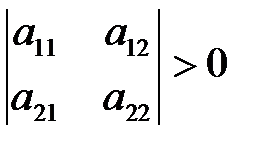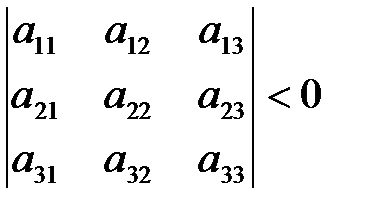, , и т.д.

Т.к. 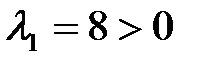, , 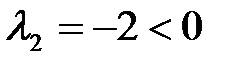то по теореме, квадратичная форма знаконеопределена. Тот же вывод можно сделать и по критерию Сильвестра, т.к. .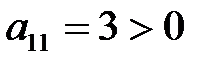

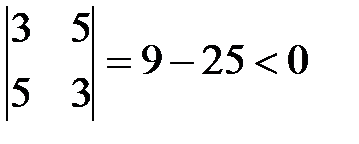4) Определение. Линия, заданная уравнением:

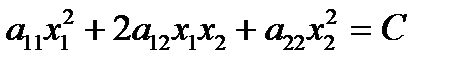, где СÎ R,

называется линией уровня квадратичной формы.

Согласно выше приведенной теореме, в ортонормированном базисе, составленном из нормированных собственных векторов матрицы A, линия уровня (9) имеет вид:

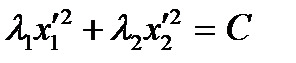, (10)

где 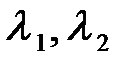- собственные значения матрицы A.

Построим линии уровня квадратичной формы для заданной матрицы A, есл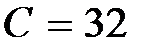и и .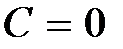

Согласно решению в пункте 2, она имеет канонический вид:

.

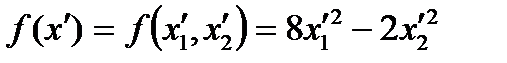При 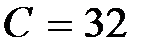линия уровня задается уравнением:

.

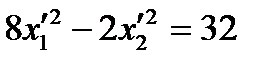Преобразуем его:

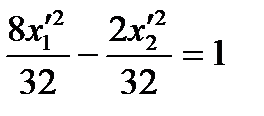или .

Это уравнение гиперболы в системе координат 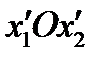, 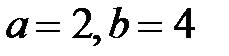- полуоси гиперболы, 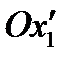- действительная ось, 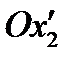- мнимая ось.

При 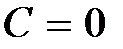линия уровня задается уравнением:

.

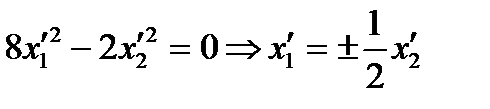Это уравнения прямых линий в системе координат 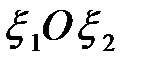(асимптоты рассмотренной выше гиперболы).
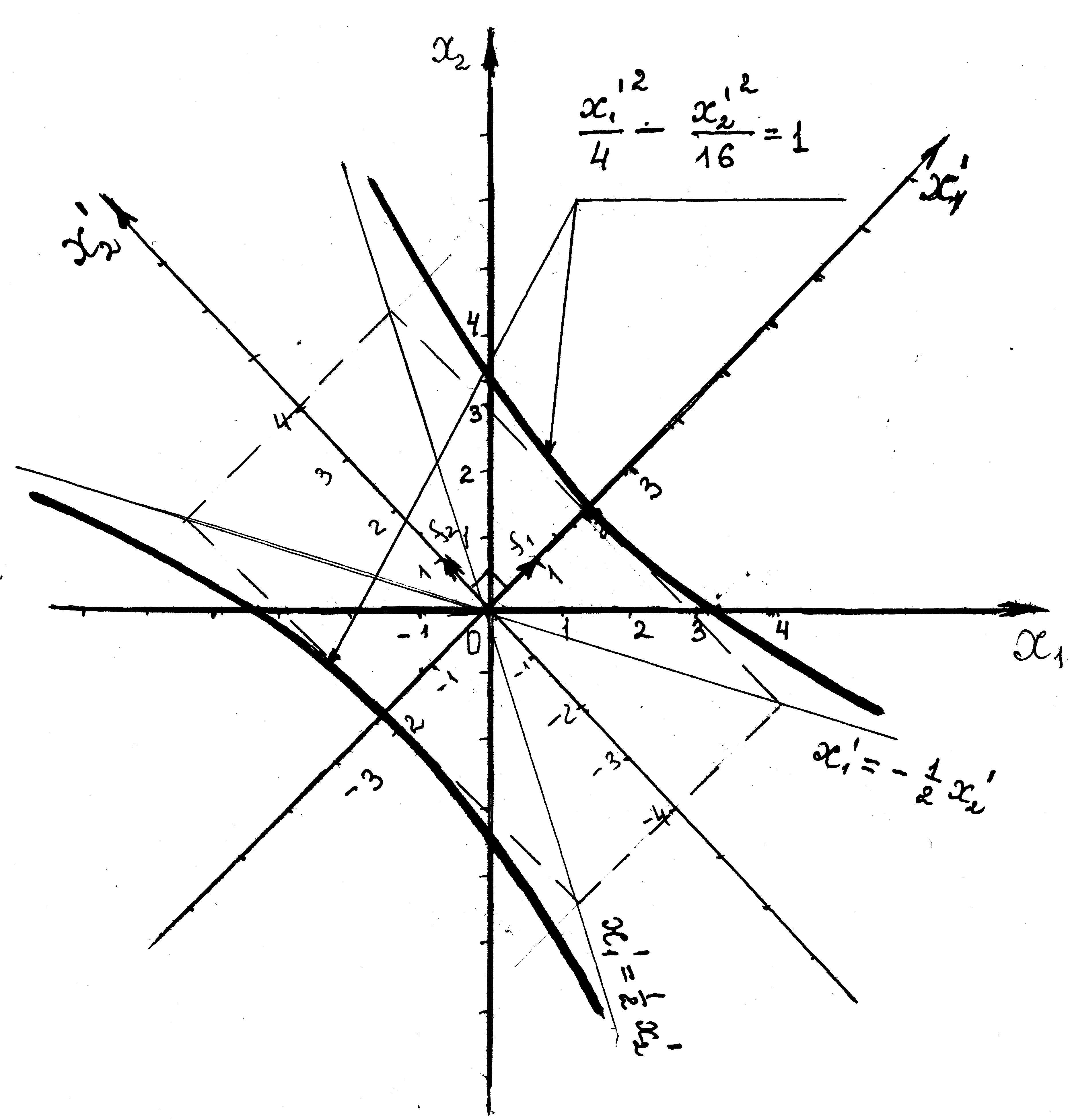