
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Решение. Матрица данной системы такова, что диагональные элементы близки к единице, а все остальные – значительно меньше единицы
|
|
Матрица данной системы такова, что диагональные элементы близки к единице, а все остальные – значительно меньше единицы. Поэтому для применения метода итераций естественно записать систему в виде
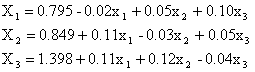
Условия сходимости для полученной системы выполнены

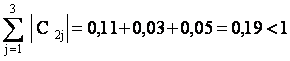
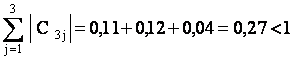
Берем в качестве начального вектора х(0) столбец свободных членов, округлив его элементы до двух знаков после запятой:
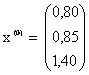
Далее последовательно находим при k = 1
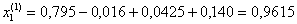
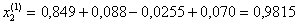
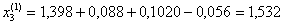
при k = 2
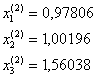
при k = 3

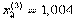
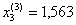
Значения неизвестных при k =2 и k = 3 отличны не более чем на 0, 003, поэтому, если в качестве приближенных значений неизвестных взять  ,
, 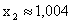 ,
,  то погрешность этих приближенных значений не превзойдет
то погрешность этих приближенных значений не превзойдет 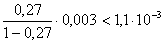
Метод отделения корней уравнений
В данной задаче 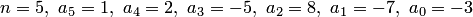 . Согласно теореме 3.1 уравнение имеет пять корней. Поскольку
. Согласно теореме 3.1 уравнение имеет пять корней. Поскольку 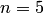 , то по следствию из теоремы 3.2 уравнение имеет по крайней мере один действительный корень.
, то по следствию из теоремы 3.2 уравнение имеет по крайней мере один действительный корень.
Оценим модули корней по теореме 3.3. Так как
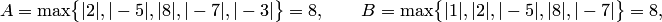
то 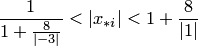 или
или 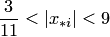 , т.е. все корни лежат внутри данного кольца. По следствию из теоремы 3.3 это означает, что положительные корни удовлетворяют неравенству
, т.е. все корни лежат внутри данного кольца. По следствию из теоремы 3.3 это означает, что положительные корни удовлетворяют неравенству 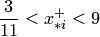 , а отрицательные — неравенству
, а отрицательные — неравенству 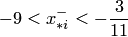 .
.
Применим теоремы 3.4 и 3.5 для уточнения приведенных результатов. Найдем верхнюю границу положительных корней. Так как 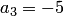 — первый отрицательный коэффициент в последовательности
— первый отрицательный коэффициент в последовательности 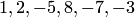 , то
, то  , а
, а 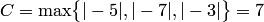 — наибольшая из абсолютных величин отрицательных коэффициентов. Следовательно,
— наибольшая из абсолютных величин отрицательных коэффициентов. Следовательно,  .
.
Найдем нижнюю границу положительных корней. Составим уравнение:
или 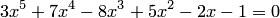 (старший коэффициент должен быть положительным). Для этого уравнения
(старший коэффициент должен быть положительным). Для этого уравнения 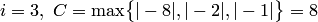 , поэтому
, поэтому 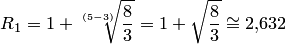 . Отсюда
. Отсюда 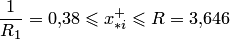 .
.
Уточним границы отрицательных корней. Составим уравнение:
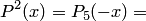 или
или  .
.
Для этого уравнения 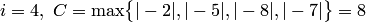 , поэтому
, поэтому 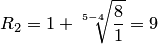 . Составим уравнение
. Составим уравнение
или  . Для этого уравнения
. Для этого уравнения 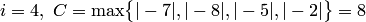 , поэтому
, поэтому 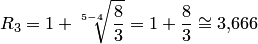 . Отсюда находим:
. Отсюда находим:  . Заметим, что данный результат совпадает с полученным ранее.
. Заметим, что данный результат совпадает с полученным ранее.
Исследуем структуру корней уравнения. Так как квадрат каждого некрайнего коэффициента больше произведения двух его соседних коэффициентов, то по теореме 3.7 необходимое условие действительности всех корней уравнения выполняется.
На основе теоремы 3.6 определим число положительных и отрицательных корней. Выписываем коэффициенты многочлена 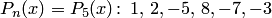 . Так как число перемен знака
. Так как число перемен знака 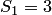 , то число положительных корней равно трем или меньше на четное число, т.е. равно 1. Далее выписываем коэффициенты многочлена
, то число положительных корней равно трем или меньше на четное число, т.е. равно 1. Далее выписываем коэффициенты многочлена 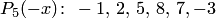 . Так как число перемен знаков
. Так как число перемен знаков 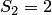 , то число отрицательных корней равно двум или меньше на четное число, т.е. их вообще нет.
, то число отрицательных корней равно двум или меньше на четное число, т.е. их вообще нет.
Метод касательных
Найти корень уравнения 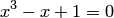 упрощенным методом Ньютона.
упрощенным методом Ньютона.
Корень уравнения отделен в примере 3.2: 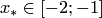 .
.
1. Выберем начальное приближение 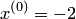 и зададим
и зададим 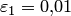 и
и 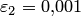 .
.
2, 3. Выполним расчеты по формуле (3.19):
Результаты расчетов приведены в табл. 3.15.
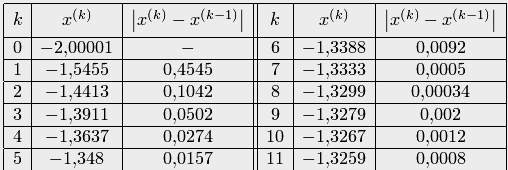
При  получено решение
получено решение  , а при
, а при  — решение
— решение 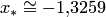 . Очевидно, по сравнению с методом Ньютона сходимость замедляется
. Очевидно, по сравнению с методом Ньютона сходимость замедляется
Метод половинного деления
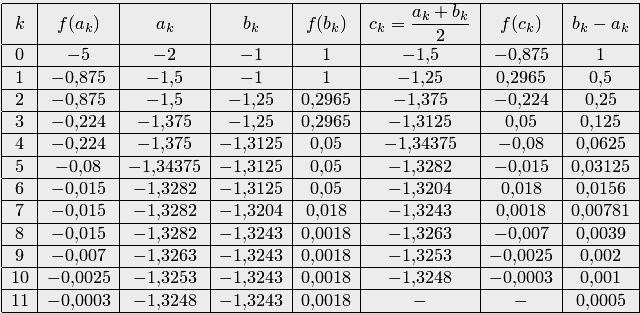
В примере 3.3 были отделены корни уравнения. Уточним корень, лежащий на отрезке 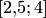 . Результаты расчетов поместим в табл. 3.2.
. Результаты расчетов поместим в табл. 3.2.
В результате найден интервал 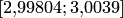 и приближенное значение корня
и приближенное значение корня 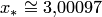 .
.
Метод половинного деления
Метод хорд
Найти корень уравнения 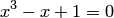 методом хорд с точностью
методом хорд с точностью 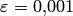 .
.
Рассмотрим задачу нахождения корня на отрезке 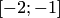 (см. пример 3.2). Так как
(см. пример 3.2). Так как 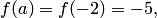
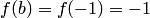 , a
, a 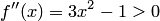 на отрезке
на отрезке 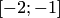 , то
, то 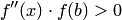 и, следовательно, имеем второй случай (см. рис. 3.7, б).
и, следовательно, имеем второй случай (см. рис. 3.7, б).
Положим 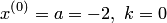 . Тогда по формуле (3.8) получаем
. Тогда по формуле (3.8) получаем
Так как 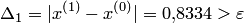 , то положим
, то положим 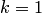 и продолжим процесс:
и продолжим процесс:
Так как 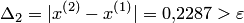 , то положим
, то положим 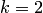 и продолжим процесс:
и продолжим процесс:
Поскольку 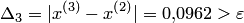 , положим
, положим 
Так как 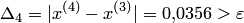 , положим
, положим 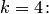
Поскольку 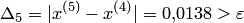 , положим
, положим 
Так как 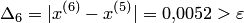 , положим
, положим 
Поскольку 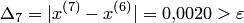 , положим
, положим 
Так как 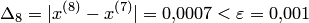 , то корень уравнения
, то корень уравнения 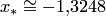 . Из анализа поведения
. Из анализа поведения  следует, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
следует, что сходимость метода хорд линейная, однако более быстрая, чем сходимость метода половинного деления.
Вывод
|
|