Передавальна функція гідроакустичного каналу

Дослідження впливу каналу зв'язку на проходження сигналу здійснюється за допомогою передавальної функції, що представляє собою оператор, що перетворить вхідний вплив лінійної системи у вихідну реакцію. Передавальна функція гідроакустичного каналу залежить від просторових координат, частоти і часу.

Сенс акустичної передавальної функції К полягає в наступному: якщо тональний сигнал з амплітудою S1 випромінюється в точці, координати якої визначаються радіус вектором, то сигнал, прийнятий в момент часу т в точці, яка визначається радіусом-вектором, буде мати вигляд

S ₂ = S ₁· К (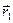, , 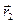ω, t)·℮ ^{iω t} (2.3)

Поглинання - вид втрат з іншим законом зміни в залежності від відстані в порівнянні з втратами при розширенні фронту хвилі.

Згідно класичної гідродинамічної теорії при поширенні акустичних хвиль у водному середовищі спостерігається поглинання звуку за рахунок дисипації енергії в в'язкої рідини. Фізична сутність вузького поглинання пов'язана з виникненням механічних напружень при деформаціях зсуву шарів рідини і незворотнім перенесенням імпульсу між ними.

Зміщена напруга пропорційно коефіцієнту динамічної (першої) в'язкості. Поширення механічної хвилі в середовищі супроводжується не тільки деформаціями зсуву, а й всебічного стиснення. При цьому порушується термодинамічна рівновага, що викликає дисипативні релаксаційні процеси, які прагнуть до відновлення цієї рівноваги. Інтенсивність процесів дисипації енергії характеризує коефіцієнт об'ємної (другий) в'язкості [4].

В'язке поглинання є домінуючим в прісній воді. У морі воно має суттєве значення лише на ультразвукових частотах. Поглинання звуку в морській воді на частотах від 5 до 50 кГц у багато разів більше, ніж у прісній, і пояснюється релаксаційною теорією Мандельштамма і Леонтовича взаємодії між молекулами рідини і розчинених у ній солей.

Релаксаційна теорія поглинання звуку є подальшим розвитком класичної і більш повно роз'яснює питання про поглинання звуку в частині, що віднесена класичною теорією до об'ємної (другий) в'язкості. Згідно релаксаційної теорії про коефіцієнт об'ємної в'язкості не можна говорити як про таку константі, оскільки її величина виявляється залежною від частоти [5].

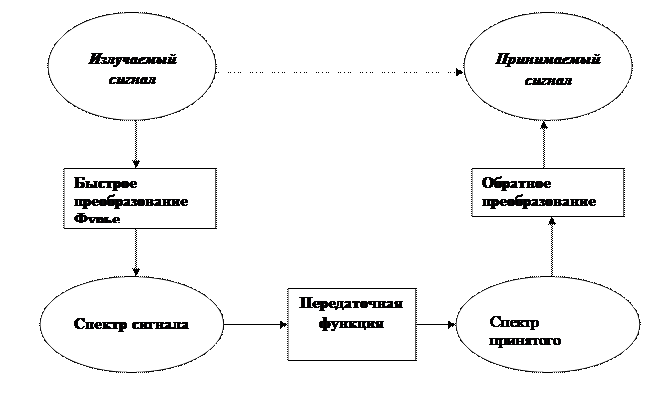
Рис.2.5 Схема розрахунку передавального тракту

Розглянемо рівняння Нав'є-Стокса, представлене у вигляді [5, 8]

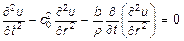, (2.4)

де u = u (r, t) - оригінал змінної, під якою можна розуміти, наприклад, звуковий тиск; с ₀ – постійна швидкість звуку; ρ – щільність води; b = (4/3)· η +ξ, η, ξ – коефіцієнти динамічної та об'ємної в'язкості відповідно; r = | 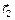- | – координата, відрахувавши від джерела u (0, t).

Перетворимо рівняння (2.4) за Лапласом при нульових початкових умовах:

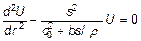. (2.5)

Тут U = U (R, S) - зображення функції і = і (г, г); S = iω - комплексна частота.

Позначимо

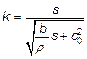. (2.6)

Рішення рівняння (2.5) шукаємо у вигляді:

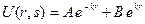(2.7)

Якщо в (4) В ¹ 0, то при r ® ¥ U ® ¥, що не відповідає умові випромінювання і не має фізичного сенсу. Звідси В = 0. Для визначення константи А застосовуємо граничні умови для місця розташування джерела сигналу і (0, т), а з урахуванням перетворення Лапласа для його зображення U (0, s). Тут r= 0, отже, U (0, s) = A і рівняння (2.7) прийме вигляд

U (r, s) = U (0, s)·℮ ^{- kr} (2.8)

Передавальна функція, відповідна рішенням (2.8) рівняння (2.4), має вигляд

К ₀(s) = U (r, s) / U (0, s) = ℮ ^{- kr} . (2.9)

Замінюючи s на iω, уявімо вираз (2.5) для коефіцієнта K у вигляді

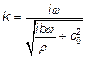
. (2.10)

З фізичних міркувань ясно, що затухання хвилі не повинно бути занадто сильним, інакше замість поширення коливань виникне аперіодичний процес. Отже, амплітуда хвилі на відстанях порядку довжини хвилі r ≈ λ повинна змінюватися слабо, тобто exp(-kλ) ≈ 1 или kλ < < 1. При розгляді малов’язких рідин, до яких відноситься вода, допущення kλ < < 1 відповідає умові:

b2ω 2/c04 ρ 2 < < 1, (2.11)

яка виконується навіть для надвисоких частот акустичних коливань ω ~ 2π •108 с-1. При виконанні умови (2.6) можливо розкласти (2.10) в ряд в околиці одиниці і, обмежуючись першими двома членами, записати [5, 8]

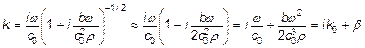. (2.11)

З (2.11) видно, що коефіцієнт до, що має фізичний зміст хвильового числа при поширенні акустичної хвилі в звуковбирною середовищі можна представити у вигляді двох доданків - хвильового числа ідеальної рідини до0 = ω / С0 і показника загасання

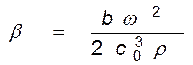. (2.12)

З формули (2.12) видно, що з точки зору класичної гідродинамічної теорії показник загасання має квадратичну залежність від частоти.