
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Полная производная сложной функции
|
|
Пусть в области 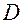 задана функция двух переменных:
задана функция двух переменных:
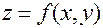 , (11)
, (11)
у которой переменные 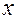 и
и 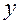 являются функциями одной переменной
являются функциями одной переменной 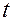 :
:
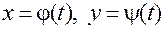
 . (12)
. (12)
Тогда 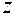 является сложной функцией одной независимой переменной
является сложной функцией одной независимой переменной 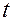 с промежуточными переменными
с промежуточными переменными 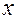 и
и 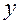 :
:
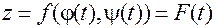 (13)
(13)
(рис. 10).
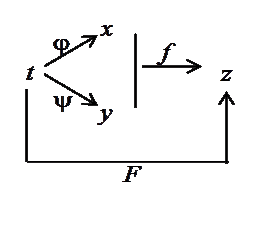
Рис. 10
Рассмотрим задачу нахождения производной 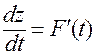 этой сложной функции на основании уравнений (11 и (12) без использования явной записи (13).
этой сложной функции на основании уравнений (11 и (12) без использования явной записи (13).
Теорема. Пусть 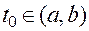 , и выполняются два условия: удовлетворяет двум условиям:
, и выполняются два условия: удовлетворяет двум условиям:
1. В окрестности точки 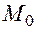
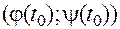 существуют частные производные
существуют частные производные 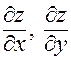 , непрерывные в самой точке
, непрерывные в самой точке 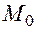 .
.
2. Функции  дифференцируемы в точке
дифференцируемы в точке 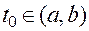 .
.
Тогда сложная функция 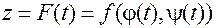 дифференцируема в точке
дифференцируема в точке 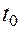 , и для ее производной справедлива формула:
, и для ее производной справедлива формула:
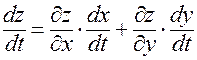 . (14)
. (14)
Доказательство. Придадим независимой переменной 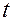 в точке
в точке 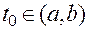 приращение
приращение 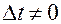 ; оно вызовет приращения
; оно вызовет приращения 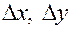 промежуточных переменных
промежуточных переменных 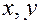 , которые в свою очередь вызовут приращение
, которые в свою очередь вызовут приращение 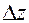 сложной функции
сложной функции 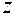 . В силу непрерывности частных производных (условие 1) к приращению
. В силу непрерывности частных производных (условие 1) к приращению 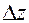 применима формула (4):
применима формула (4):
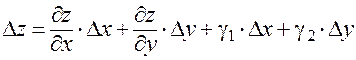 ,
,
откуда, деля на 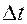 , получаем:
, получаем:
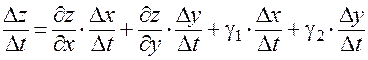 . (15)
. (15)
Здесь 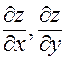 — постоянные величины для фиксированной точки
— постоянные величины для фиксированной точки  . Далее, функции
. Далее, функции 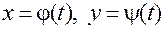 , будучи дифференцируемыми в точке
, будучи дифференцируемыми в точке 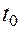 , являются также и непрерывными в этой точке, так что
, являются также и непрерывными в этой точке, так что
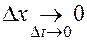 ,
, 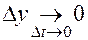 ,
,
а тогда и величины 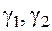 в представлении (15) также стремятся к нулю.
в представлении (15) также стремятся к нулю.
Переходя в равенстве (15) к пределу при 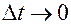 , получаем:
, получаем:
 ,
,
и далее, на основании свойств предела:
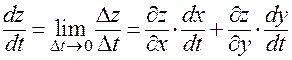 .
.
Пример. Пусть 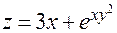 , где
, где 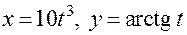 . Тогда
. Тогда
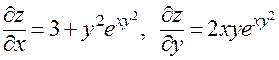 .
.
Далее,
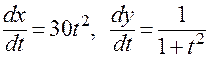 .
.
Поэтому
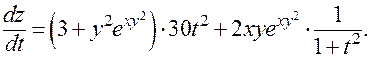
Рассмотрим теперь случай, когда у функции двух переменных 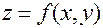 одна из переменных, например
одна из переменных, например 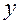 , является функцией другой:
, является функцией другой: 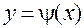 . Тогда
. Тогда 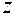 оказывается сложной функцией от
оказывается сложной функцией от 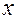 с двумя промежуточными переменными
с двумя промежуточными переменными 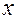 и
и 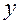 .
.
Этот случай сводится к последней теореме, если считать, что обе промежуточные переменные являются функциями одной независимой переменной 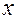 , которая в этом последнем случае играет роль переменной
, которая в этом последнем случае играет роль переменной 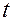 :
:
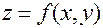 , (16)
, (16)
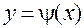 , (17)
, (17)
так что
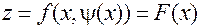 , (18)
, (18)
причем функция 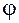 в общей схеме (12) является «тождественной»:
в общей схеме (12) является «тождественной»: 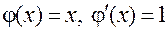 .
.
Формула (14) при этом преобразуется к виду:
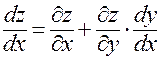 . (19)
. (19)
Отметим, что полная производная 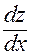 в левой части (19) определяется функцией (18), а частная производная
в левой части (19) определяется функцией (18), а частная производная 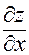 в первом слагаемом правой части ― функцией (16).
в первом слагаемом правой части ― функцией (16).
Пример. Пусть 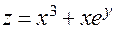 , причем
, причем 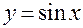 . Тогда
. Тогда
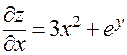 ,
, 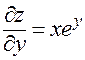 ,
, 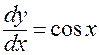 .
.
Поэтому
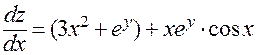 .
.
|
|