Основные понятия теории оптимизации

Задача оптимизации заключается в том, что заданы множество Х и функция f(x), определенная на X; требуется найти точки минимума или максимума функции f(x) на X. Общий вид задачи оптимизации может быть сформулирован следующим образом:
f(x) → min, x ∈ X.
h_k(x) = 0, k=1,..., K
g_j(x) ≥ 0, j=1,..., J
При этом f будем называть целевой функцией, X - допустимым множеством, любой элемент x ∈ X - допустимой точкой задачи, h_k(x) - ограничениями типа равенства, а g_j(x) - ограничениями типа неравенств.
Необходимо дать понятие минимума, т.е. той точки, которая является решением оптимизационной задачи
Определение. Глобальным минимумом f(x) называется точка x* такая что: f(x*) ≤ f(x) для любого x∈ X.
Если мы заменим слово " минимум" на " максимум", а в неравенстве поменяем знак, то мы получим определение глобального максимума.
Точки минимума или максимума еще называют экстремальными точками, а задачи - экстремальными задачами.
Различают задачи безусловной оптимизации и задачи условной оптимизации. Задача безусловной оптимизации имеет вид:
f(x) → min, x ∈ X.
Рассмотрим методы решения задач безусловной оптимизации.
^ Задачи безусловной оптимизации для функций одной переменной
Согласно наиболее простому определению, функция 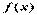представляет собой правило, которое позволяет каждому значению 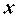поставить в соответствие единственное значение 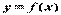. В этом случае носит название независимой переменной, а 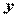- зависимой переменной.
Ряд физических процессов можно описать (или построить модели этих процессов) с помощью непрерывных функций, т.е. функций, которые обладают свойством непрерывности в каждой точке , принадлежащей областям их определения.
Определение. Функция f, определенная на выпуклом множестве X⊂ Rⁿ, называется выпуклой, если
f( λ x¹ + (1- λ )x²) ≤ λ f(x¹) + (1- λ )f(x²)

при всех x¹, x² ∈ X, λ ∈ [0, 1].
Определение. Функция называется вогнутой, если функция -f является выпуклой.
Рисунок: Пример выпуклой и вогнутой функции.
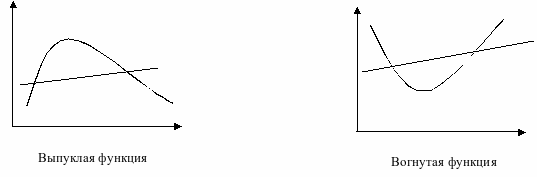