
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Глава 5
|
|
ПОГРЕШНОСТИ АНАЛИТИЧЕСКИХ
ОПРЕДЕЛЕНИЙ И ИХ ОЦЕНКА
Наряду с аналитическими характеристиками, такими как селективность (разрешающая способность), предел обнаружения, интервал определяемых содержаний, продолжительность и трудоемкость определений, методы анализа оценивают метрологическими параметрами. К ним относят правильность, воспроизводимость (точность) н сходимость результатов анализа. Изучение метрологических параметров методов анализа является самостоятельной задачей важнейшего раздела аналитической химии, выделяемого под названием хемометрики. Совместное рассмотрение аналитических и метрологических характеристик позволяет оценить информативность метода и сравнить методы анализа, выбрать наиболее адекватный метод. Математическая обработка результатов анализа, проводимая с целью расчета и оценки метрологических параметров, основана на применении математической статистики и, в частности, дисперсионного, факторного и регрессионного анализа.
5.1. ВИДЫ ПОГРЕШНОСТЕЙ
Целью определения того или иного компонента в пробе является установление его истинного содержания —  . Однако эта задача может быть решена на практике лишь с тем или иным приближением, так как величина единичного определения
. Однако эта задача может быть решена на практике лишь с тем или иным приближением, так как величина единичного определения  , полученная в результате выполнения анализа, всегда отличается от истинной
, полученная в результате выполнения анализа, всегда отличается от истинной 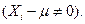 Эту разницу между найденным и истинным результатами называют абсолютной погрешностью (ошибкой), или единичным отклонением
Эту разницу между найденным и истинным результатами называют абсолютной погрешностью (ошибкой), или единичным отклонением 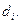 Абсолютные погрешности выражают в единицах измеряемых величин. Погрешность может быть выражена и в относительных величинах (в %):
Абсолютные погрешности выражают в единицах измеряемых величин. Погрешность может быть выражена и в относительных величинах (в %):
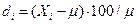
В соответствии с математической статистикой единичный результат может отличаться от истинного в принципе на любую величину, поэтому для уменьшения неопределенности всегда выполняют серию из n параллельных определений, а результат выражают в виде среднего арифметического значения  , которое является математическим ожиданием
, которое является математическим ожиданием  для выборки из n вариант:
для выборки из n вариант:
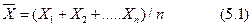
При этом  в
в  раз более точен по сравнению с
раз более точен по сравнению с  . Так как истинное значение
. Так как истинное значение  определяемого содержания обычно неизвестно, то результат анализа
определяемого содержания обычно неизвестно, то результат анализа  сравнивают с действительным значением a этой величины. За действительное значение измеряемой величины обычно принимают рассчитанное содержание определяемого компонента (в случае анализа химически чистого вещества), его содержание в стандартном образце или результат определения, полученный при помощи стандартного метода анализа.
сравнивают с действительным значением a этой величины. За действительное значение измеряемой величины обычно принимают рассчитанное содержание определяемого компонента (в случае анализа химически чистого вещества), его содержание в стандартном образце или результат определения, полученный при помощи стандартного метода анализа.
В аналитической практике выделяют три разновидности погрешностей, которые могут искажать результаты анализов при проявлении причин различной природы: случайные погрешности, систематические погрешности и промахи. Случайные погрешности обусловлены неявными факторами, меняющимися от опыта к опыту, и характеризуют понятие воспроизводимости метода (методики) анализа. Систематическая погрешность обусловлена причинами известной природы (или же причинами, которые могут быть выявлены при детальном рассмотрении методики). Ей соответствует понятие «правильность метода анализа». Понятие «точность» объединяет воспроизводимость и правильность метода анализа. Разница между случайными и систематическими отклонениями (di) заключается в том, что первые могут принимать различные значения с различными знаками, и для выборки достаточно большого объема число положительных отклонений должно быть равно числу отрицательных, вторые постоянны как по значению, так и по знаку, хотя постоянство их по значению может быть абсолютным или относительным. Наконец, третий вид погрешности — промах — представляет собой отклонение, которое резко отличается по значению от других отклонений выборки и причиной которого является невнимательность или некомпетентность аналитика. Промахи и систематические ошибки, присутствующие в выборке результатов анализа, выявляются в результате ее статистической обработки.
Результаты химического анализа, наряду с результатами любых других измерений, могут рассматриваться как случайные. Случайными могут считаться и присущие этим результатам погрешности. Свойства случайных величин описываются законами математической статистики, в соответствии с которыми выборка вариант, состоящая из результатов анализа или их погрешностей, характеризуется определенной вероятностью Р и объемом n, или кратностью анализа.
Выборка — дискретная, конечнозначная и ограниченная величина с неравномерным распределением составляющих ее вариант. Дискретность обусловливается точностью результата, конечнозначность — ограниченным значением n и интервалом определяемых концентраций (например, от О до 100%). Для малых выборок неравномерность распределения вариант неочевидна, однако при n≥ 20-30 можно заметить, что большая их доля группируется около среднего арифметического, а значительные отклонения от него редки. Причем чем больше отклонение, тем реже оно встречается, т.е. тем меньше его вероятность. То же самое можно отнести и к интервалу возможных значений случайных величин.
Математические ожидания ( ) для выборок различных объемов не совпадают точно так же, как и доли вариант в них, имеющих одинаковые знаки отклонений. Различие между случайной и систематической погрешностями становится несколько условным. Так, систематические погрешности, выявленные на фоне меньшей выборки, могут стать случайными на фоне большей, т. е. можно считать, что различие между систематической и случайной погрешностями зависит от их соотношения, вероятностей и объема выборки.
) для выборок различных объемов не совпадают точно так же, как и доли вариант в них, имеющих одинаковые знаки отклонений. Различие между случайной и систематической погрешностями становится несколько условным. Так, систематические погрешности, выявленные на фоне меньшей выборки, могут стать случайными на фоне большей, т. е. можно считать, что различие между систематической и случайной погрешностями зависит от их соотношения, вероятностей и объема выборки.
Первичной задачей статистической обработки результатов анализа является оценка надежности среднего арифметического  , проверка наличия или отсутствия погрешности и выявление, а затем и исключение промахов. Последующая задача статистической обработки результатов заключается в улучшении метрологических характеристик метода анализа, в сравнении методов анализа и т.д., т.е. она носит исследовательский характер. Статистические исследования могут, например, проводиться в следующих направлениях.
, проверка наличия или отсутствия погрешности и выявление, а затем и исключение промахов. Последующая задача статистической обработки результатов заключается в улучшении метрологических характеристик метода анализа, в сравнении методов анализа и т.д., т.е. она носит исследовательский характер. Статистические исследования могут, например, проводиться в следующих направлениях.
1. С целью уменьшения случайной погрешности (улучшение воспроизводимости) результатов анализа. Для этого могут быть проведены оценки погрешностей отдельных этапов анализа, выявлены этапы с максимальными погрешностями, изучены условия проведения отдельных этапов анализа и предложены их варианты с меньшими погрешностями, что в конечном счете приведет к уменьшению ошибки результата анализа в целом.
2. С целью устранения систематических погрешностей (улучшение правильности).
3. С целью сравнения качества работы (по точности результатов анализа) двух приборов, аналитиков, лабораторий при определении того или иного компонента в веществе по стандартной методике анализа, т.е. для проверки сходимости результатов анализа.
4. С целью сравнения результатов различных методов анализа. Практическим результатом метрологических исследований является усовершенствование известных методов анализа, аттестация новых, выбор адекватного метода для конкретного объекта, аттестация стандартных образцов, приборов, качества работы аналитиков или аналитических лабораторий.
5.2. ОЦЕНКА СЛУЧАЙНЫХ ОТКЛОНЕНИЙ
Случайные отклонения результатов, характеризующие воспроизводимость методов анализа, являются статистическими величинами и определяются неявными факторами, изменяющимися от опыта к опыту. Воспроизводимость зависит от объема выборки и может быть точно найдена только при  Необходимо также отметить, что
Необходимо также отметить, что  при отсутствии систематической погрешности. Оценка воспроизводимости выборки, состоящей из nвариант, может быть проведена различными способами.
при отсутствии систематической погрешности. Оценка воспроизводимости выборки, состоящей из nвариант, может быть проведена различными способами.
1. Среднее отклонение — среднее арифметическое отдельных отклонений:

2. Отклонение от медианы. Медиана М представляет собой тот единичный результат выборки, по отношению к которому число меньших и больших значений равно. Если число вариант четное, то медиану находят как среднее арифметическое значение из двух центральных величин. Медиана лучше характеризует центр распределения малой выборки, чем среднее арифметическое, так как не испытывает влияния одной или двух больших ошибок, если они располагаются по одну сторону от нее.
Отклонение от моды. Мода — значение величины, наиболее часто встречающейся в выборке. Она пригодна для выборок относительно небольших объемов и для чисел, содержащих 2 или 3 значащие цифры. При симметричном распределении мода тождественна с  и М.
и М.
Диапазон выборки, или размах варьирования  , который представляет собой разницу между максимальным и минимальным значениями.
, который представляет собой разницу между максимальным и минимальным значениями.
Дисперсия и стандартное отклонение результатов. Эти критерии применяют наиболее часто для оценки воспроизводимости, так как имеют теоретическое обоснование и являются наиболее точной ее характеристикой. Стандартное отклонение выборки S вычисляют по уравнениям:

В выражении (5.4) число степеней свободы равно числу вариант, так как известно истинное значение среднего, что возможно при анализе стандартных образцов или химически чистых веществ. Величину под корнем называют дисперсией V. Стандартное отклонение выражают в абсолютных значениях величин измеренных вариант выборки, она носит приближенный характер. При 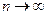 величина
величина  . Величина
. Величина  представляет собой истинное значение стандартного отклонения генеральной совокупности (генеральное стандартное отклонение), а значит, и истинную характеристику воспроизводимости метода анализа. На практике S может быть заменена на
представляет собой истинное значение стандартного отклонения генеральной совокупности (генеральное стандартное отклонение), а значит, и истинную характеристику воспроизводимости метода анализа. На практике S может быть заменена на  при
при  ,
,
Стандартное отклонение зависит в ряде случаев от определяемой концентрации, поэтому более правильно характеризовать воспроизводимость метода анализа для определенного интервала содержаний определяемого компонента, обрабатывая результаты нескольких выборок для проб с различным содержанием определяемого компонента. Однако совместная статистическая обработка выборок может быть корректна только в том случае, если различия между ними носят случайный характер и они являются приближенной оценкой одной генеральной совокупности. Такие выборки называют равноточными, а полученное в результате совместной обработки стандартное отклонение называют средневзвешенным стандартным отклонением. Проверку равноточности выборок можно провести их попарным сравнением при помощи критерия Фишера (F-критерий) и t-критерия при заданном уровне значимости *.
* Совместное одновременное сравнение равноточности нескольких выборок проводят также по критерию Бартлета 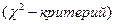 если n каждой выборки ≥ 6, или по критерию Кохрана (G-критерий), если объемы выборок равны [1].
если n каждой выборки ≥ 6, или по критерию Кохрана (G-критерий), если объемы выборок равны [1].
Пример такого сравнения будет рассмотрен ниже. Если имеется т проб и для каждой выполнено по n А параллельных определений, то для расчета средневзвешенной стандартной погрешности применяют следующую формулу:
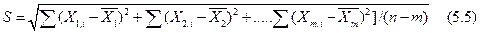
где Xi — результат для m пробы;  — средний результат для m пробы; n — число всех определений (n-mnA); n-m — число степеней свободы.
— средний результат для m пробы; n — число всех определений (n-mnA); n-m — число степеней свободы.
Стандартное отклонение может быть выражено в виде относительной величины 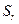 , которую называют коэффициентом вариации. Так, для выборки примера 1
, которую называют коэффициентом вариации. Так, для выборки примера 1 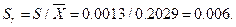 Относительное стандартное отклонение выражают в виде величины с одной значащей цифрой. Абсолютное или относительное стандартное отклонение может меняться при переходе от одного интервала определяемых концентраций к другому. Однако закономерностей, общих для всех методов анализа, при этом не установлено. В ряде случаев между абсолютной стандартной погрешностью и концентрацией С установлена приближенная зависимость
Относительное стандартное отклонение выражают в виде величины с одной значащей цифрой. Абсолютное или относительное стандартное отклонение может меняться при переходе от одного интервала определяемых концентраций к другому. Однако закономерностей, общих для всех методов анализа, при этом не установлено. В ряде случаев между абсолютной стандартной погрешностью и концентрацией С установлена приближенная зависимость
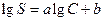
где а и Ь — постоянные величины, причем a≈ 0, 5.
Химические методы анализа характеризуются постоянным и небольшим значением абсолютной стандартной погрешности в широком интервале определяемых содержаний, а атомно-эмиссионный спектральный анализ, например, характеризуется стабильной относительной стандартной погрешностью. Вблизи предела обнаружения для всех методов анализа происходит резкий рост относительной стандартной погрешности.
5.3. СТАТИСТИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ПОГРЕШНОСТЕЙ. ПРЕДЕЛ ОБНАРУЖЕНИЯ
При 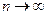 распределение результатов определений и их случайных погрешностей соответствует в большинстве случаев нормированному стандартному распределению Гаусса — Лапласа, которое описывает как вероятность (долю) Р самого результата X, так и вероятность (долю) Р той или иной величины его погрешности а в общем числе результатов или погрешностей (рис. 5.1). Площадь, получаемая при интегрировании кривой в пределах
распределение результатов определений и их случайных погрешностей соответствует в большинстве случаев нормированному стандартному распределению Гаусса — Лапласа, которое описывает как вероятность (долю) Р самого результата X, так и вероятность (долю) Р той или иной величины его погрешности а в общем числе результатов или погрешностей (рис. 5.1). Площадь, получаемая при интегрировании кривой в пределах  а следовательно, двусторонняя доверительная вероятность (Р) всех результатов равна единице. При построении кривой распределения результатов по оси абсцисс по обе стороны от среднего результата
а следовательно, двусторонняя доверительная вероятность (Р) всех результатов равна единице. При построении кривой распределения результатов по оси абсцисс по обе стороны от среднего результата  откладывают величины
откладывают величины  а при построении кривой распределения погрешностей по обе стороны от нулевой погрешности откладывают величины
а при построении кривой распределения погрешностей по обе стороны от нулевой погрешности откладывают величины 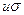 . По оси ординат откладывают вероятность a результата X или его погрешности
. По оси ординат откладывают вероятность a результата X или его погрешности  . Здесь u — коэффициент интегрирования, выраженный числом единиц
. Здесь u — коэффициент интегрирования, выраженный числом единиц 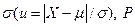 — двусторонняя доверительная вероятность и a— односторонняя доверительная вероятность, причем P=2a.
— двусторонняя доверительная вероятность и a— односторонняя доверительная вероятность, причем P=2a.
Если проводить интегрирование в пределах от  до
до  то внутри интервала интегрирования находится 100Р процентов результатов от бесконечного числа результатов измерений. Двусторонняя доверительная вероятность Р представляет собой, таким образом, долю результатов (или погрешностей) от их общего числа, для которых стандартная погрешность не превышает
то внутри интервала интегрирования находится 100Р процентов результатов от бесконечного числа результатов измерений. Двусторонняя доверительная вероятность Р представляет собой, таким образом, долю результатов (или погрешностей) от их общего числа, для которых стандартная погрешность не превышает 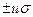 . Для результатов (или их погрешностей), которые не попадают в рассматриваемый интервал, вводят понятие доли риска, или уровня значимости, b=1-P. Чем больше принятая доля риска b для единичного результата анализа или интервала результатов, тем меньше максимальная погрешность
. Для результатов (или их погрешностей), которые не попадают в рассматриваемый интервал, вводят понятие доли риска, или уровня значимости, b=1-P. Чем больше принятая доля риска b для единичного результата анализа или интервала результатов, тем меньше максимальная погрешность 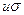 и, соответственно, коэффициент интегрирования u, характеризующие погрешность результата, и тем больше возможность завысить точность результата.
и, соответственно, коэффициент интегрирования u, характеризующие погрешность результата, и тем больше возможность завысить точность результата.
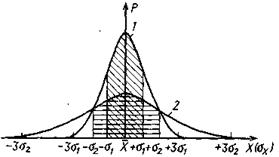
Рис. 5.1. Кривые нормального распределения 
Заштрихованные площади соответствуют 68, 26% результатов погрешностей при u=1
Иногда в аналитической практике погрешность считают промахом, а результат исключается из генеральной совокупности или выборки при b=0.003 (P=0.997 и u=3.09). Это так называемый трехсигмовый критерий уровня значимости. Чаще используют двухсигмовый критерий, тогда b=0.046 (P=0.954 и u=2.09). Последний является более жестким при выявлении промахов или систематических погрешностей, так как из генеральной совокупности (выборки) исключается большее число вариант, и менее жестким при оценке точности результатов различных генеральных совокупностей, так как при сравнении исключаются большие погрешности. Выбор того или иного уровня значимости позволяет переводить результаты анализа из случайных в неслучайные (т. е. вызванные неслучайной причиной) и, соответственно, погрешности этих результатов из разряда случайных в разряд промахов или систематических погрешностей. Конкретный выбор b зависит от практической цели анализа и степени важности полученного результата. С точки зрения математической статистики, строгость (надежность) полученного в лаборатории результата анализа тем выше, чем больше доверительная вероятность Р, примененная при его оценке, так как при этом в выборку включаются все более отклоняющиеся от среднего арифметического  варианты и уменьшается вероятность потерять случайные большие погрешности.
варианты и уменьшается вероятность потерять случайные большие погрешности.
Обычно в аналитической химии применяют доверительную вероятность Р = 0, 95 или двухсигмовый критерий, но в особо важных случаях, например при анализе лекарственных препаратов, принимают Р = 0, 99. На практике превалирует стремление не потерять большие случайные погрешности, что может привести к необоснованному завышению точности, над риском включить в результат анализа промахи или систематические погрешности.
Вероятность Р единичного результата анализа определяет предел интегрирования и или максимальное значение 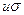 , на которое этот результат может отличаться от
, на которое этот результат может отличаться от  , поэтому и сам единичный результат анализа имеет смысл только при указании интервала значений, в пределах которого он может изменяться. Этот интервал погрешностей
, поэтому и сам единичный результат анализа имеет смысл только при указании интервала значений, в пределах которого он может изменяться. Этот интервал погрешностей 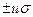 , соответствующий принятому Р, называют доверительным интервалом:
, соответствующий принятому Р, называют доверительным интервалом: 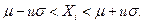
Величина aдолжна быть при этом точно известна, как, например, при выполнении определений стандартным методом анализа. Аналогичные рассуждения относятся и к среднему арифметическому, доверительный интервал которого равен 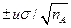 , где
, где 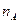 — число параллельных определений
— число параллельных определений
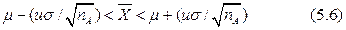
Таблица 5.1. Значение вероятностей a стандартного нормированного распределения
| u | a | u | a | ||
| 0, 01 | 0, 0040 | 1, 00 | 0, 3413 | ||
| 0, 05 | 0, 0199 | 1, 50 | 0, 4332 | ||
| 0, 10 | 0, 0398 | 2, 00 | 0, 4772 | ||
| 0, 20 | 0, 0793 | 2, 50 | 0, 4938 | ||
| 0, 30 | 0, 1179 | 3, 00 | 0, 49865 | ||
| 0, 40 | 0, 1554 | 3, 40 | 0, 49966 | ||
| 0, 50 | 0, 1915 | 4, 00 | 0, 499968 | ||
| 0, 75 | 0, 2734 | 5, 00 | 0, 499997 |
Величина  без указания доверительного интервала лишена смысла. Чем больше Р и, следовательно, чем больше u при
без указания доверительного интервала лишена смысла. Чем больше Р и, следовательно, чем больше u при 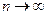 (генеральная совокупность), тем большее число результатов с большими ошибками попадает в доверительный интервал: при u=1 величина P=68.3%; при u=1.96 Р=95%, при u=3.00 P=99.74%. Для нормированного стандартного распределения Гаусса — Лапласа при известной генеральной стандартной ошибке
(генеральная совокупность), тем большее число результатов с большими ошибками попадает в доверительный интервал: при u=1 величина P=68.3%; при u=1.96 Р=95%, при u=3.00 P=99.74%. Для нормированного стандартного распределения Гаусса — Лапласа при известной генеральной стандартной ошибке  легко найти доверительные вероятности a, когда случайная погрешность отдельного определения не превысит
легко найти доверительные вероятности a, когда случайная погрешность отдельного определения не превысит 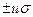 (табл. 5.1), причем для симметричного интервала (u1-u2) P=2a, для асимметричного двустороннего
(табл. 5.1), причем для симметричного интервала (u1-u2) P=2a, для асимметричного двустороннего 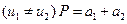 и для интервала с двумя значениями одного знака
и для интервала с двумя значениями одного знака 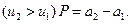 Оценка такого же рода для максимальных случайных погрешностей среднего результата проводится в соответствии с выражением
Оценка такого же рода для максимальных случайных погрешностей среднего результата проводится в соответствии с выражением 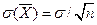 .
.
Для выборок с  для оценки
для оценки 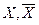 и их погрешностей используют кривую t-распределения, которая по сравнению с кривой Гаусса является более пологой и тем более, чем меньше число вариант nв выборке, т.е. вероятность больших погрешностей среди их общего числа увеличивается с уменьшением числа вариант. Кроме того, для t-распределения
и их погрешностей используют кривую t-распределения, которая по сравнению с кривой Гаусса является более пологой и тем более, чем меньше число вариант nв выборке, т.е. вероятность больших погрешностей среди их общего числа увеличивается с уменьшением числа вариант. Кроме того, для t-распределения  При одной и той же вероятности Р коэффициенты пределов интегрирования кривых t-распределения всегда больше коэффициентов кривой нормального распределения. Коэффициенты t-распределения, или коэффициенты распределения Стьюдента, зависят, таким образом, и от вероятности Р, и от числа вариант n. Доверительный интервал среднего арифметического выборки рассчитывают по формуле
При одной и той же вероятности Р коэффициенты пределов интегрирования кривых t-распределения всегда больше коэффициентов кривой нормального распределения. Коэффициенты t-распределения, или коэффициенты распределения Стьюдента, зависят, таким образом, и от вероятности Р, и от числа вариант n. Доверительный интервал среднего арифметического выборки рассчитывают по формуле

Коэффициенты интегрирования t при выборочном интегрировании приведены в табл. 5.2.
Таблица 5.2. Коэффициенты Стьюдента t
| Число вариант n | Число степеней свободы f = n - 1 | Значения t при Р | ||
| 0, 90 | 0, 95 | 0, 99 | ||
| 6, 314 | 12, 71 | 65, 66 | ||
| 2, 920 | 4, 303 | 9, 925 | ||
| 2, 353 | 3, 182 | 5, 841 | ||
| 2, 132 | 2, 776 | 4, 604 | ||
| 2, 015 | 2, 571 | 4, 034 | ||
| 1, 94 | 2, 45 | 3, 71 | ||
| 1, 90 | 2, 37 | 3, 50 | ||
| 1, 86 | 2, 31 | 3, 36 | ||
| 1, 83 | 2, 26 | 3, 25 | ||
| 1, 81 | 2, 23 | 3, 17 | ||
| 1, 75 | 2, 13 | 2, 95 | ||
| 1, 73 | 2, 09 | 2, 85 |
Уравнение (5.7) может быть использовано и для характеристики предела обнаружения того или иного определяемого компонента пробы. Предел обнаружения данной методики анализа — минимальное количество (концентрация) компонента, которое может быть обнаружено с той или иной вероятностью Р. При уменьшении концентрации определяемого вещества в пробе наступает момент, когда аналитическая реакция уже не приводит к ожидаемому внешнему эффекту с доверительной вероятностью, равной единице. Например, при Р = 0, 5 только 50% всех результатов положительны, причем при дальнейшем уменьшении концентрации компонента Р уменьшается. То же самое относится и к любому аналитическому сигналу.
На рис. 5.2 приведены кривые нормального распределения результатов определения для различных критериев предельно низких количеств (концентраций) вещества. Открываемому минимуму 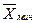 соответствует кривая 2, которая характеризуется доверительной вероятностью Р = 0, 5, так как кривая распределения результатов холостого опыта
соответствует кривая 2, которая характеризуется доверительной вероятностью Р = 0, 5, так как кривая распределения результатов холостого опыта 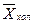 (кривая 1) перекрывает ее наполовину. В данном случае с вероятностью Р = 0, 5 имеется риск «переоткрыть» определяемый компонент, приняв сигнал холостого опыта за аналитический сигнал (погрешность второго рода). Кривая распределения результатов 3 соответствует пределу обнаружения
(кривая 1) перекрывает ее наполовину. В данном случае с вероятностью Р = 0, 5 имеется риск «переоткрыть» определяемый компонент, приняв сигнал холостого опыта за аналитический сигнал (погрешность второго рода). Кривая распределения результатов 3 соответствует пределу обнаружения 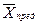 данной аналитической реакции. Предел обнаружения — количество (концентрация) определяемого вещества, которое может быть обнаружено с достаточно большой вероятностью Р. В данном случае Р = 0, 997 (трехсигмовый критерий). Так как кривая 3 все же перекрывается кривой 1 холостого опыта, можно принять сигнал определяемого вещества за сигнал холостого опыта, т.е. «недооткрыть» вещество (погрешность первого рода).
данной аналитической реакции. Предел обнаружения — количество (концентрация) определяемого вещества, которое может быть обнаружено с достаточно большой вероятностью Р. В данном случае Р = 0, 997 (трехсигмовый критерий). Так как кривая 3 все же перекрывается кривой 1 холостого опыта, можно принять сигнал определяемого вещества за сигнал холостого опыта, т.е. «недооткрыть» вещество (погрешность первого рода).
Если считать, что погрешности первого и второго рода распределены по нормальному закону и что  то критерии значимости b погрешностей первого и второго рода также равны: b=1-(0.5+0.4986)=0.0014 в случае
то критерии значимости b погрешностей первого и второго рода также равны: b=1-(0.5+0.4986)=0.0014 в случае 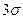 -критерия. Однако распределение результатов и их погрешностей вблизи предела обнаружения может не подчиняться нормальному закону распределения и
-критерия. Однако распределение результатов и их погрешностей вблизи предела обнаружения может не подчиняться нормальному закону распределения и 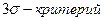 дает тогда значительно большие значения b. Для точного определения предела обнаружения необходимо установить (построить) кривые распределения результатов (погрешностей) холостого опыта и определяемого компонента для его концентраций, близких к пределу обнаружения, что является достаточно трудоемкой задачей.
дает тогда значительно большие значения b. Для точного определения предела обнаружения необходимо установить (построить) кривые распределения результатов (погрешностей) холостого опыта и определяемого компонента для его концентраций, близких к пределу обнаружения, что является достаточно трудоемкой задачей.

Рис. 5.2. Кривые нормального распределения предельно низких концентраций веществ (или их погрешностей): 1 — холостой сигнал, 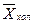 2— открываемый минимум,
2— открываемый минимум, 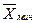 3— предел обнаружения
3— предел обнаружения 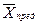 , II — области погрешностей первого и второго рода для предела обнаружения.
, II — области погрешностей первого и второго рода для предела обнаружения.
Природа холостого сигнала может быть различна: наложение других аналитических сигналов, инструментальные шумы, загрязненность реактивов определяемым компонентом (реактивная погрешность). Последняя особенно часто наблюдается при определении низких концентраций таких распространенных элементов, как железо, кремний, кальций, натрий и некоторых других. Реактивную ошибку можно учесть или с помощью «холостого» опыта (определение выполняют по принятой методике анализа, но без анализируемого вещества), результат которого вычитается из результата определения, или путем использования «холостого» раствора в качестве раствора сравнения в инструментальных методах анализа.
Если принять, что для рис. 5.2 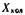 — содержание определяемого компонента, вносимого с реактивами, то
— содержание определяемого компонента, вносимого с реактивами, то

так как после вычитания из суммарного результата содержания определяемого компонента, внесенного в пробу с реактивами 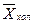 , остается искомая величина. Из приведенных выражений видно, что предел обнаружения не зависит от результата холостого опыта, а определяется только его абсолютной стандартной погрешностью
, остается искомая величина. Из приведенных выражений видно, что предел обнаружения не зависит от результата холостого опыта, а определяется только его абсолютной стандартной погрешностью  . Однако увеличение результата «холостого» опыта обычно влечет за собой и увеличение его погрешности, поэтому при росте загрязненности реактивов определяемым компонентом предел обнаружения будет ухудшаться. Предел обнаружения при данной стандартной ошибке
. Однако увеличение результата «холостого» опыта обычно влечет за собой и увеличение его погрешности, поэтому при росте загрязненности реактивов определяемым компонентом предел обнаружения будет ухудшаться. Предел обнаружения при данной стандартной ошибке  можно уменьшить, увеличивая число параллельных определений:
можно уменьшить, увеличивая число параллельных определений:

Этот путь может быть использован в случае применения быстрых автоматических методов анализа в сочетании с обработкой результатов на ЭВМ, когда число параллельных определений 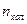 может быть доведено до n·102.
может быть доведено до n·102.
Если холостой сигнал отсутствует, 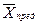 будет определяться абсолютной погрешностью для нижнего предела определяемых данным методом содержаний (концентраций). Так, для титриметрического метода анализа в идеальном случае можно считать, что его абсолютная погрешность постоянна для широкого интервала объема титранта и определяется капельной погрешностью бюретки, т.е. равна объему капли
будет определяться абсолютной погрешностью для нижнего предела определяемых данным методом содержаний (концентраций). Так, для титриметрического метода анализа в идеальном случае можно считать, что его абсолютная погрешность постоянна для широкого интервала объема титранта и определяется капельной погрешностью бюретки, т.е. равна объему капли 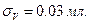 Для надежного фиксирования по бюретке минимального объема титранта на уровне З
Для надежного фиксирования по бюретке минимального объема титранта на уровне З  -критерия доверительной вероятности необходимо, чтобы объем был хотя бы в 3 раза больше
-критерия доверительной вероятности необходимо, чтобы объем был хотя бы в 3 раза больше 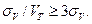 В этом случае относительная погрешность равна
В этом случае относительная погрешность равна 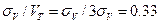 (или 33%), а предел обнаружения титруемого вещества может быть рассчитан по минимальному объему титранта (0, 09 мл) с минимально возможной концентрацией реагента. Присутствие в анализируемом растворе примесей, титруемых в данных условиях вместе с определяемым компонентом, будет вносить в результат систематическую погрешность и увеличивать предел обнаружения.
(или 33%), а предел обнаружения титруемого вещества может быть рассчитан по минимальному объему титранта (0, 09 мл) с минимально возможной концентрацией реагента. Присутствие в анализируемом растворе примесей, титруемых в данных условиях вместе с определяемым компонентом, будет вносить в результат систематическую погрешность и увеличивать предел обнаружения.
5.4. ИСКЛЮЧЕНИЕ ПРОМАХОВ ИЗ ВЫБОРКИ
При небрежной работе аналитика полученные результаты не будут вариантами генеральной совокупности и должны быть из нее исключены, так как в противном случае среднее арифметическое значение и стандартная погрешность будут искажаться, В случае выборки результатов и трехсигмовой доверительной вероятности промахом считается результат, для которого отклонение  если принят более жесткий двухсигмовый критерий (Р = 0, 95), то для промаха
если принят более жесткий двухсигмовый критерий (Р = 0, 95), то для промаха 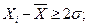 и в этом случае доля риска b составляет уже 0, 05 (5%), а не 0, 003 (0, 3%). Иногда для обнаружения в выборке промаха сначала рассчитывают значение S для всех вариант, выбрасывают из выборки результат, который при выбранной доверительной вероятности оказался промахом, снова рассчитывают S, исключают варианты, которые не попадают в новую выборку, и т.д., пока промахи не будут отсутствовать.
и в этом случае доля риска b составляет уже 0, 05 (5%), а не 0, 003 (0, 3%). Иногда для обнаружения в выборке промаха сначала рассчитывают значение S для всех вариант, выбрасывают из выборки результат, который при выбранной доверительной вероятности оказался промахом, снова рассчитывают S, исключают варианты, которые не попадают в новую выборку, и т.д., пока промахи не будут отсутствовать.
Таблица 5.3. Табличные коэффициенты QT
| Число вариант п | Значения QT при Р | ||
| 0, 90 | 0, 95 | 0, 99 | |
| 3. | 0, 94 | 0, 98 | 0, 99 |
| 0, 76 | 0, 85 | 0, 93 | |
| 0, 64 | 0, 73 | 0, 82 | |
| 0, 56 | 0, 64 | 0, 74 | |
| 0, 51 | 0, 59 | 0, 68 | |
| 0, 47 | 0, 54 | 0, 63 | |
| 0, 44 | 0, 51 | 0, 60 | |
| 0, 41 | 0, 48 | 0, 57 |
Рассмотренный путь выявления промахов длительный. Проще выявить промахи можно, используя статистические критерии, например Q-тест (критерий). Варианты выборки располагают для этого в порядке возрастания и путем деления разности подвергаемой сомнению и соседней с ней вариант на диапазон выборки находят расчетное значение Qp
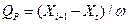
которое затем сравнивают с табличным значением 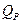 . Если
. Если 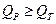 (табл. 5.3), то проверяемый результат является промахом и его отбрасывают. Для выборки из трех вариант проверку начинают с наименьшего значения. Если при этом наименьшее значение подлежит исключению, то дополнительно выполняют еще одно-два определения, применяют Qтест к новой выборке при отсутствии промаха и рассчитывают среднее арифметическое. При n> 3 первой проверяют наибольшую варианту. Если она является промахом, то ее исключают, затем находят диапазон для новой выборки и для нее проверяют уже наименьшее значение и т.д.
(табл. 5.3), то проверяемый результат является промахом и его отбрасывают. Для выборки из трех вариант проверку начинают с наименьшего значения. Если при этом наименьшее значение подлежит исключению, то дополнительно выполняют еще одно-два определения, применяют Qтест к новой выборке при отсутствии промаха и рассчитывают среднее арифметическое. При n> 3 первой проверяют наибольшую варианту. Если она является промахом, то ее исключают, затем находят диапазон для новой выборки и для нее проверяют уже наименьшее значение и т.д.
5.5. СРАВНЕНИЕ ДВУХ ВЫБОРОК.
ОБНАРУЖЕНИЕ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ
Надежность и объективность полученных результатов анализа — одни из основных условий, позволяющие делать выводы при решении производственных и научных проблем. Определения того или иного компонента в пробах при этом могут быть выполнены в разное время, на различных приборах, разными аналитиками, в различных лабораториях, наконец, различными методами анализа, в том числе и вновь разработанными, и т.д. Поэтому тождественность полученных значений  при различных условиях должна быть строго оценена. Статистическая оценка результатов анализа является относительной и заключается в сравнении в первую очередь стандартных погрешностей двух выборок, одна из которых является как бы эталонной, и затем — в сравнении средних арифметических значений. Однородность выборок, т. е. их принадлежность к одной генеральной совокупности, проверяют с помощью F-критерия (критерий Фишера). Если выборки однородны, то сравнивают их средние арифметические при помощи t-критерия. Вывод об однородности или неоднородности двух сравниваемых при помощи F-критерия выборок, или ответ на вопрос, одинакова или неодинакова их стандартная погрешность, имеют большое практическое значение и позволяют решить задачи, требующие оценки точности сравниваемых вариантов. В качестве примеров приведем следующие.
при различных условиях должна быть строго оценена. Статистическая оценка результатов анализа является относительной и заключается в сравнении в первую очередь стандартных погрешностей двух выборок, одна из которых является как бы эталонной, и затем — в сравнении средних арифметических значений. Однородность выборок, т. е. их принадлежность к одной генеральной совокупности, проверяют с помощью F-критерия (критерий Фишера). Если выборки однородны, то сравнивают их средние арифметические при помощи t-критерия. Вывод об однородности или неоднородности двух сравниваемых при помощи F-критерия выборок, или ответ на вопрос, одинакова или неодинакова их стандартная погрешность, имеют большое практическое значение и позволяют решить задачи, требующие оценки точности сравниваемых вариантов. В качестве примеров приведем следующие.
Оценить точность результатов определений, полученных двумя аналитиками, т.е. качество их работы; оценить точность результатов, полученных для различных приборов, сравнивать качество работы двух аналитических лабораторий и т.д.
Оценить точность нового метода анализа или точность определений того или иного компонента в объекте, анализируемом впервые при помощи стандартной методики путем сравнения исследуемой выборки с выборкой результатов анализа стандартных образцов.
Контролировать качество выполнения серийных анализов, анализируя время от времени стандартные образцы, и т.д.
4. Оценить влияние на воспроизводимость изменения тех или иных условий анализа (изменения тех или иных параметров методики анализа).
5. Решить задачу о наличии или отсутствии зависимости стандартной погрешности от определяемого интервала (концентрации). Если в пределах исследуемого интервала содержаний подтверждается однородность выборок, то вычисляют средневзвешенную стандартную погрешность по формуле (5.5), которая важна для метрологической оценки метода анализа в целом.
Если однородность сравниваемых выборок доказана, то можно оценить статистическую неразличимость средних арифметических величин при помощи  критерия или, наоборот, их различие в зависимости от решаемой практической задачи. Во втором случае подтверждается гипотеза о влиянии на исследуемый среднеарифметический результат систематической погрешности, если вторая выборка получена в результате анализа стандартных образцов (тогда
критерия или, наоборот, их различие в зависимости от решаемой практической задачи. Во втором случае подтверждается гипотеза о влиянии на исследуемый среднеарифметический результат систематической погрешности, если вторая выборка получена в результате анализа стандартных образцов (тогда  может быть заменена на
может быть заменена на  или по стандартной методике анализа. Например, сделать вывод о наличии или отсутствии систематической погрешности в среднем арифметическом исследуемого метода анализа (нового или с измененными параметрами) можно, сравнивая его со средним арифметическим равноточного с ним стандартного метода.
или по стандартной методике анализа. Например, сделать вывод о наличии или отсутствии систематической погрешности в среднем арифметическом исследуемого метода анализа (нового или с измененными параметрами) можно, сравнивая его со средним арифметическим равноточного с ним стандартного метода.
Сравнение дисперсий двух выборок при помощи F-критерия (критерия Фишера) проводят следующим образом. Получают расчетное значение критерия Fp по формуле:
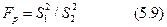
помещая в числителе большую из дисперсий. По таблице (табл. 5.4) находят теоретическое значение FT. Если FP< FT, выборки принадлежат одной генеральной совокупности и, следовательно, равноточны. Число степеней свободы большей дисперсии  и, соответственно, для меньшей дисперсии
и, соответственно, для меньшей дисперсии  . Обращает на себя внимание, что FT сильнее зависит от числа степеней свободы выборки с меньшей стандартной погрешностью S2, т.е. имеющей большую точность, а также его значительное различие для двух приведенных доверительных вероятностей при одинаковых степенях свободы. Доверительная вероятность Р=0, 95 является более жесткой, так как исключает из генеральной совокупности меньшую разницу вариант. Поэтому равноточность двух выборок, полученная при Р=0, 99, может оказаться недоказанной при Р=0, 95.
. Обращает на себя внимание, что FT сильнее зависит от числа степеней свободы выборки с меньшей стандартной погрешностью S2, т.е. имеющей большую точность, а также его значительное различие для двух приведенных доверительных вероятностей при одинаковых степенях свободы. Доверительная вероятность Р=0, 95 является более жесткой, так как исключает из генеральной совокупности меньшую разницу вариант. Поэтому равноточность двух выборок, полученная при Р=0, 99, может оказаться недоказанной при Р=0, 95.
Сравнение средних арифметических двух выборок после доказательства их равноточности выполняют в последовательности. Сначала рассчитывают tP (коэффициент Стьюдента) для данного числа степеней свободы  по формулам:
по формулам:

где

Таблица 5.4. Теоретические значения критерия Фишера (FT)
| f2 | Значения FT при f1 | ||||
| P = 0, 95 | |||||
| 19, 00 | 19, 16 | 19, 25 | 19, 30 | 19, 33 | |
| 9, 55 | 9, 28 | 9, 12 | 9, 01 | 8, 94 | |
| 6, 94 | 6, 59 | 6, 39 | 6, 26 | 6, 16 | |
| 5, 79 | 5, 41 | 5, 19 | 5, 05 | 4, 95 | |
| 5, 14 | 4, 76 | 4, 53 | 4, 39 | 4, 28 | |
| P = 0, 99 | |||||
| 99, 00 | 99, 17 | 99, 25 | 99, 30 | 99, 33 | |
| 30, 81 | 29, 46 | 28, 71 | 28, 24 | 27, 91 | |
| 18, 00 | 16, 69 | 15, 98 | 15, 52 | 15, 21 | |
| 13, 27 | 12, 06 | 11, 39 | 10, 97 | 10, 67 | |
| 10, 92 | 9, 78 | 9, 15 | 8, 75 | 8, 47 |
Полученное значение tp сравнивают с теоретическим значением tT (см. табл. 5.2) для выбранного уровня доверительной вероятности Р. Если tp< tT, то расхождение между 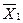 и
и 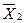 вызвано случайными погрешностями, обусловленными воспроизводимостью при условиях сравниваемых выборок и, следовательно, систематическая погрешность отсутствует. Если необходимо оценить отклонение
вызвано случайными погрешностями, обусловленными воспроизводимостью при условиях сравниваемых выборок и, следовательно, систематическая погрешность отсутствует. Если необходимо оценить отклонение  от теоретического содержания
от теоретического содержания  (анализ химически чистого вещества или стандартного образца), то вычисление tp упрощается:
(анализ химически чистого вещества или стандартного образца), то вычисление tp упрощается:

При отсутствии химически чистых или стандартных проб в первом приближении величинами, близкими к  , можно считать среднее арифметическое результатов определения данного компонента в одной и той же пробе, полученное стандартным методом при n
, можно считать среднее арифметическое результатов определения данного компонента в одной и той же пробе, полученное стандартным методом при n 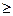 20 и отсутствии систематической погрешности.
20 и отсутствии систематической погрешности.
5.6. КЛАССИФИКАЦИЯ СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ. КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ
Любой метод анализа включает ряд этапов (операций), и каждому из них присущи свои случайные и систематические погрешности. Систематические погрешности отдельного этапа анализа могут быть положительными или отрицательными, их причины устанавливают с той или иной степенью легкости, и поэтому имеется возможность их оценки или устранения посредством усовершенствования методики. Если систематическая погрешность меньше случайной погрешности, служащей для аттестации метода анализа на принятом уровне доверительной вероятности, то считают, что систематическая погрешность в данном методе анализа отсутствует. В противном случае она должна быть учтена при расчете результата или в ходе выполнения определения. Систематические погрешности разнообразны по своей природе и в той или иной мере специфичны для каждого метода. Их классификация основана на различных принципах. 1. В зависимости от влияния количества (массы) определяемого вещества погрешности подразделяют на постоянные (аддитивные) и линейно изменяющиеся (пропорциональные, мультипликативные). В первом случае систематическая погрешность не коррелирует с количеством определяемого компонента, во втором она пропорциональна ему. К постоянной систематической погрешности приводит, например, загрязнение реактивов определяемым компонентом (реактивная погрешность), а к линейно изменяющейся — погрешность в определении характеристик титранта 2. В зависимости от степени причинной обоснованности природы систематических погрешностей и возможности их учета выделяют: а) систематические погрешности известной природы, они могут быть рассчитаны и затем учтены путем введения соответствующей поправки; б) систематические погрешности известной природы, которые неизвестны, но могут быть учтены в методике анализа; в) систематические погрешности невыясненной природы, которые неизвестны.
К погрешностям типа aможно отнести погрешность взвешивания на воздухе, температурные погрешности определения объема и массы тел, индикаторные погрешности в титриметрии и т.д. К систематическим погрешностям типа б приводит разница между номинальным и реальным объемами мерной посуды (колбы, пипеткн, бюретки), несоответствие состава и физико-химических свойств эталонов и проб, загрязнение реактивов и т.д. Они могут быть учтены, например, при калибровке мерной посуды, при выполнении холостого определения, при тщательном выборе эталонных образцов. Наконец, систематические погрешности типа в, наиболее трудно выясняемые на практике, могут быть устранены только после детальных метрологических исследований и, в частности, только после учета остальных, видов погрешностей. Часто при этом необходимо рассмотреть более широкий круг явлений, чем обычно принимаемых в расчет, могущих быть причиной систематических отклонений: продолжительность приготовления растворов, температура окружающей среды и ее колебания, загрязнение атмосферы и т.д. Наличие корреляции между влияющим фактором и систематической погрешностью устанавливают путем расчета коэффициента корреляции 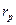 :
:
. 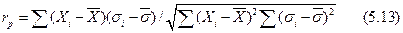
где  ,
,  — среднее арифметическое значений исследуемого фактора и стандартной погрешности;
— среднее арифметическое значений исследуемого фактора и стандартной погрешности;  ,
, 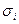 — одновременно или близко по времени измеренная пара значений влияющего фактора и стандартной погрешности.
— одновременно или близко по времени измеренная пара значений влияющего фактора и стандартной погрешности.
Так как стандартная погрешность является средней величиной, то реально наряду с влияющим фактором измеряют 4—5 значений аналитического сигнала. Коэффициент корреляции изменяется в пределах —1< r< +1 и является статистической величиной. Поэтому наличие корреляции может быть оценено с той или иной доверительной вероятностью Р. Корреляция наблюдается, если гр (расчетное значение) больше 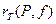 где f=n-2, так как одновременно измеряются два значения, а n — число пар измерений (табл. 5.5). Для надежной корреляции n должно составлять 8—10.
где f=n-2, так как одновременно измеряются два значения, а n — число пар измерений (табл. 5.5). Для надежной корреляции n должно составлять 8—10.
Таблица 5.5. Значения коэффициента корреляции 
| f = n-2 | Р = 0, 95 | f = n-2 | Р = 0, 95 | ||
| 1, 00 | 0, 71 | ||||
| 0, 95 | 0, 67 | ||||
| 0, 88 | 0, 63 | ||||
| 0, 81 | 0, 60 | ||||
| 0, 75 | 0, 58 |
5.7. СЛОЖЕНИЕ СЛУЧАЙНЫХ И СИСТЕМАТИЧЕСКИХ ПОГРЕШНОСТЕЙ. ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ АНАЛИЗА
Случайные погрешности отдельных стадий анализа влияют на его окончательный результат в соответствии с законом распространения погрешностей.
1. Если окончательный результат является суммой или разностью измерений на промежуточных этапах, то происходит сложение дисперсий случайных погрешностей:

где 1, 2,....., i — порядковый номер стадии анализа.
В соответствии с выражением (5.14) на случайную абсолютную погрешность окончательного результата наибольшее влияние будет оказывать погрешность наименее воспроизводимого этапа.
2. Если окончательный результат является произведением или частным результатов промежуточных этапов, то при этом суммируют квадраты относительных случайных погрешностей:

5.8. ПОГРЕШНОСТИ НЕКОТОРЫХ МЕТОДОВ АНАЛИЗА
5.8.1. Гравиметрический метод
Относительная суммарная случайная ошибка гравиметрического метода может быть рассчитана по выражению

где  — абсолютная погрешность массы определяемого вещества, г; g— масса определяемого вещества, г;
— абсолютная погрешность массы определяемого вещества, г; g— масса определяемого вещества, г; 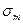 — погрешность взятия навески, г; m — навеска анализируемого вещества, г;
— погрешность взятия навески, г; m — навеска анализируемого вещества, г; 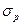 — погрешность взятия весовой формы, г; р — масса весовой формы, г.
— погрешность взятия весовой формы, г; р — масса весовой формы, г.
 * Коэффициент
* Коэффициент 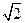 в значениях относительных случайных погрешностей появляется вследствие того, что массу навески анализируемого вещества или массу весовой формы получают как разность результатов двух взвешиваний: масса бюкса с веществом минус масса бюкса с остатками вещества.
в значениях относительных случайных погрешностей появляется вследствие того, что массу навески анализируемого вещества или массу весовой формы получают как разность результатов двух взвешиваний: масса бюкса с веществом минус масса бюкса с остатками вещества.
 |
При массе весовой формы 0, 5 г в случае кристаллического осадка и массе анализируемого вещества, например, 1 г относительную случайную погрешность рассчитывают по формуле (5.16).
Если принять, что 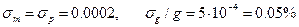 . Однако обычно массы навески и весовой формы несколько меньше (р = 0, 1 г — для аморфных осадков и 0, 5 г — для кристаллических), поэтому погрешность гравиметрического метода на практике составляет 0, 1%. В лучших же случаях она может достигать 0, 01%. Так как
. Однако обычно массы навески и весовой формы несколько меньше (р = 0, 1 г — для аморфных осадков и 0, 5 г — для кристаллических), поэтому погрешность гравиметрического метода на практике составляет 0, 1%. В лучших же случаях она может достигать 0, 01%. Так как  и если навеска m и масса весовой формы р являются величинами одного порядка, то увеличение аналитического множителя
и если навеска m и масса весовой формы р являются величинами одного порядка, то увеличение аналитического множителя  приводит к уменьшению суммарной погрешности вследствие или увеличения навески (фиксирована масса весовой формы), или весовой формы (фиксирована навеска). Благодаря высокой точности гравиметрический метод часто используют для аттестации эталонных образцов или как арбитражный. Систематические погрешности в гравиметрическом методе возникают за счет растворимости осадка при его осаждении и промывании, вследствие загрязненности реактивов, при работе с открытой посудой (разбрызгивание, пыль), взвешивании недостаточно охлажденных тиглей и т.д. В итоге в конкретном гравиметрическом методе сумма систематических погрешностей должна быть меньше случайной погрешности.
приводит к уменьшению суммарной погрешности вследствие или увеличения навески (фиксирована масса весовой формы), или весовой формы (фиксирована навеска). Благодаря высокой точности гравиметрический метод часто используют для аттестации эталонных образцов или как арбитражный. Систематические погрешности в гравиметрическом методе возникают за счет растворимости осадка при его осаждении и промывании, вследствие загрязненности реактивов, при работе с открытой посудой (разбрызгивание, пыль), взвешивании недостаточно охлажденных тиглей и т.д. В итоге в конкретном гравиметрическом методе сумма систематических погрешностей должна быть меньше случайной погрешности.
5.8.2. Прямой титриметрический метод
Так как окончательный результат титриметрического определения получается при использовании математических действий умножения и деления, то относительная случайная погрешность результата может быть рассчитана по формуле

где V — расход титранта, мл;  —абсолютная стандартная погрешность измерения объема титранта, мл; С — молярная концентрация раствора титранта:
—абсолютная стандартная погрешность измерения объема титранта, мл; С — молярная концентрация раствора титранта: 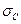 — абсолютная стандартная погрешность определения молярности; остальные обозначения — см. уравнение (5.16).
— абсолютная стандартная погрешность определения молярности; остальные обозначения — см. уравнение (5.16).
Из выражения видно, что для достижения минимальной относительной случайной погрешности титриметрического определения необходимо, чтобы навеска, объем титранта и его молярная концентрация были возможно большими. Для бюретки вместимостью 25, 00 мл и молярной концентрации титранта 0, 1 М расход титранта при расчете навески для титриметрического определения принимают равным 20 мл. При использовании аналитических весов погрешность 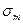 взвешивания составляет
взвешивания составляет 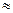 0, 2 мг. Навеску m берут как разность масс бюкса с веществом и пустого бюкса:
0, 2 мг. Навеску m берут как разность масс бюкса с веществом и пустого бюкса:  m=mк-mн. Так как mк≈ mн вследствие того что масса навески незначительна по сравнению с массой бюкса, то в соответствии с законом распространения ошибок:
m=mк-mн. Так как mк≈ mн вследствие того что масса навески незначительна по сравнению с массой бюкса, то в соответствии с законом распространения ошибок:
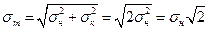
Если принять 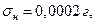 то
то 
Аналогично можно рассчитать абсолютную стандартную погрешность  измерения объема титранта. Если Принять
измерения объема титранта. Если Принять  (примерный объем капли), то
(примерный объем капли), то 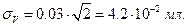 Абсолютная стандартная погрешность определения молярной концентрации титранта является погрешностью эталонирования, так как в титриметрии количество (содержание) определяемого вещества определяется относительно количества вещества титранта, израсходованного на полное протекание аналитической реакции. Вследствие этого тот или иной метод анализа не может быть более точным, чем точность приготовления используемого в нем эталона.
Абсолютная стандартная погрешность определения молярной концентрации титранта является погрешностью эталонирования, так как в титриметрии количество (содержание) определяемого вещества определяется относительно количества вещества титранта, израсходованного на полное протекание аналитической реакции. Вследствие этого тот или иной метод анализа не может быть более точным, чем точность приготовления используемого в нем эталона.
Используемые для сравнения образцы веществ характеризуются классом точности и имеют различные названия. Стандартные образцы различных веществ изготавливаются международными и национальными службами и соответствуют наиболее высокому классу точности. В титриметрии им соответствуют фиксаналы. Эталоны по химическому составу изготавливают предприятия или аналитические лаборатории. Качество их аттестации ниже, чем стандартов. Наконец, часто эталонами могут быть химически чистые вещества (в титриметрии — установочные вещества). Эталонные растворы готовят сами аналитики. В титриметрии отношение  должно быть меньше 0, 001 (< 0, 1%). Тогда относительная случайная погрешность титриметрического метода для m = 0, 1 г и V=20 мл:
должно быть меньше 0, 001 (< 0, 1%). Тогда относительная случайная погрешность титриметрического метода для m = 0, 1 г и V=20 мл:
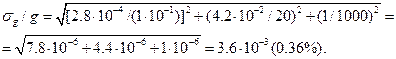
Видно, что максимальные погрешности вносят операции взвешивания вещества и измерения объема титранта. Их можно уменьшить, увеличивая разность отсчетов для аналитических весов и бюретки, т.е. увеличивая навеску и объем титранта V. Приведенный расчет относится к методу отдельных навесок. В методе пипетирования к указанным выше погрешностям прибавляют погрешность отбора аликвотных частей пипеткой, и суммарная погрешность титрования будет больше. Уменьшить погрешность измерения объема титранта можно, переходя к микробюреткам, имеющим меньшую цену деления, однако при этом уменьшается и объем титранта, который помещают в бюретку.
Индикаторная погрешность титриметрических методов является систематической. Она может быть как аддитивной, так и мультипликативной. Например, в методе кислотно-основного титрования в случае сильных протолитов выделяют «протонную» ошибку, которая не зависит от концентрации титруемого протолита кислотного характера:

Аналогична ей и гидроксильная ошибка, если в конечной точке титрования имеется избыток сильного основания:
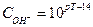
где рТ — показатель титрования применяемого индикатора.
Абсолютные значения этих систематических погрешностей не зависят от исходной концентрации сильной кислоты или сильного основания. Знак погрешности в данном случае отражает несоответствие конечной точки титрования и точки эквивалентности, т.е. недотитрован (минус) или перетитрован (плюс) анализируемый раствор. При титровании слабых кислот или слабых оснований индикаторная погрешность является пропорциональной (мультипликативной):
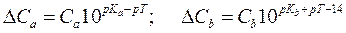
Индикаторная погрешность в методе окислительно-восстановительного титрования с использованием обратимых окислительно-восстановительных индикаторов является постоянной и определяется близостью потенциала перехода окраски индикатора к потенциалу в точке эквивалентности рассматриваемой системы. В прямом комплексонометрическом титровании индикаторная погрешность
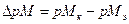
где  — концентрация свободных ионов металла в конечной точке титрования;
— концентрация свободных ионов металла в конечной точке титрования;  — их концентрация в точке эквивалентности.
— их концентрация в точке эквивалентности.
Относительная индикаторная ошибка 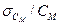 (в %) может быть рассчитана по формуле
(в %) может быть рассчитана по формуле
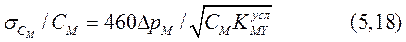
где  — аналитическая концентрация иона металла;
— аналитическая концентрация иона металла; 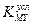 — словная константа устойчивости комплекса металла с комплексоном.
— словная константа устойчивости комплекса металла с комплексоном.
Из уравнения видно, что относительная ошибка тем меньше, чем выше устойчивость комплекса и общая концентрация титруемого иона металла. С удачно выбранным индикатором при визуальном титровании  обычно составляет
обычно составляет 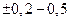 единиц и при
единиц и при  моль/л,
моль/л, 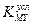 должна быть ≈ 107 чтобы относительная погрешность не превышала 1%. При
должна быть ≈ 107 чтобы относительная погрешность не превышала 1%. При  моль/л и тех же остальных условиях относительная погрешность не превышает уже 0, 1 %. Эти условия хорошо соблюдаются, например, при визуальном титровании раствором ЭДТА ионов магния при рН = 10 с индикатором эриохром черный Т. Уравнение (5.18) не учитывает ионы металла, еще связанные с индикатором в точке эквивалентности, однако это несущественно, если
моль/л и тех же остальных условиях относительная погрешность не превышает уже 0, 1 %. Эти условия хорошо соблюдаются, например, при визуальном титровании раствором ЭДТА ионов магния при рН = 10 с индикатором эриохром черный Т. Уравнение (5.18) не учитывает ионы металла, еще связанные с индикатором в точке эквивалентности, однако это несущественно, если  значительно превышает аналитическую концентрацию индикатора.
значительно превышает аналитическую концентрацию индикатора.
Физические и физико-химические методы анализа имеют в значительной степени общие виды погрешностей с химическими методами, так как включают такие операции, как взвешивание, измерение объема, разделение компонентов перед конечным определением, концентрирование и т. д., однако им присущи и собственные виды случайных и систематических погрешностей. Особенности погрешностей физических и физико-химических методов анализа определяются, с одной стороны, большим разнообразием природы используемых в них аналитических сигналов, а с другой — широким применением измерительной аппаратуры. Они будут рассмотрены во втором томе учебника.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Чарыков А. К. Математическая обработка результатов химического анализа. Л.: Химия, 1984. 168 с.
Доерфель К- Статистика в аналитической химии. М.: Мир, 1969. 248 с.
Алексеев Р. И., Коровин Ю. И. Руководство по вычислению и обработке результатов количественного анализа. М.: Атомиздат, 1972. 72 с.
Шаевич А. Б. Аналитическая служба как система. М.: Химия, 1981. 264 с.
|
|