💸 Как сделать бизнес проще, а карман толще?

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое раписание, но и напоминать клиентам о визитах тоже. Проблема в том, что средняя цена по рынку за такой сервис — 800 руб/мес или почти 15 000 руб за год. И это минимальный функционал. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
⚡️ Для новых пользователей первый месяц бесплатно. А далее 290 руб/мес, это в 3 раза дешевле аналогов. За эту цену доступен весь функционал: напоминание о визитах, чаевые, предоплаты, общение с клиентами, переносы записей и так далее.
✅ Уйма гибких настроек, которые помогут вам зарабатывать больше и забыть про чувство «что-то мне нужно было сделать».
Сомневаетесь? нажмите на текст, запустите чат-бота и убедитесь во всем сами!

Прямая геодезическая задача

В геодезии часто приходится передавать координаты с одной точки на другую. Например, зная исходные координаты точки А (рис.23), горизонтальное расстояние SAB от неё до точки В и направление линии, соединяющей обе точки (дирекционный угол α AB или румб rAB), можно определить координаты точки В. В такой постановке передача координат называется прямой геодезической задачей.

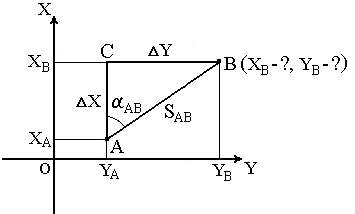
Рис. 23. Прямая геодезическая задача

Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.

Дано: Точка А(XA, YA), SAB иα AB.

Найти: точку В(XB, YB).

Непосредственно из рисунка имеем:

Δ X = XB – XA;

Δ Y = YB – YA.

Разности Δ X и Δ Y координат точек последующей и предыдущей называются приращениями координат. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:

Δ X = SAB · cos α AB;

Δ Y = SAB · sin α AB.

Так как в этих формулах SAB всегда число положительное, то знаки приращений координат Δ X и Δ Y зависят от знаков cos α AB и sin α AB. Для различных значений углов знаки Δ X и Δ Y представлены в табл.1.

Таблица 1. Знаки приращений координат Δ X и Δ Y

При помощи румба приращения координат вычисляют по формулам:

Δ X = SAB · cosrAB;

Δ Y = SAB · sin rAB.

Знаки приращениям дают в зависимости от названия румба.

Вычислив приращения координат, находим искомые координаты другой точки:

XB = XA + Δ X;

YB = YA+ Δ Y.

Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения.