Практическое занятие 1. Тема: Случайные погрешности и методы их исключения.

Задание. Изучите точечные и интервальные оценки законов распределения результатов наблюдений и оценки распределения случайных погрешностей. Ознакомьтесь с критериями исключения грубых погрешностей.

Методические рекомендации. Обратить внимание на меры, принимаемые для исключения систематических погрешно­стей из результатов прямых многократных наблюдений.

Случайные погрешности и методы их исключения. Точечные оценки законов распределения результатов наблюдений. При анализе дискретных случайных величин возникает за­дача о нахождении точечных оценок параметров их функции распределе­ния на основании выборок - ряда значений Х_i, принимаемых случайной величиной Х в n - независимых опытах.

Оценку параметра называют точечной, если она выражается од­ним числом. К точечным характеристикам погрешности относятся СКО случайной погрешности и среднее арифметическое значение из­меряемой величины.

Оценим математическое ожидание m₁ и СКО 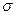для ограниченной группы (выборки) наблюдений, обозначив их через .

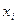Результат измерений при распределении наблюдений по нормальному закону определяют, учитывая известную в теории вероятностей закономерность (теория больших чисел): при достаточно большом числе n независимых наблюдений 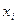среднее арифметическое значений случайной величины приближается к ее математическому ожиданию m₁, определяемому подобно оценке по формуле (3.8) (см. лекцию3):

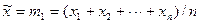
Соответственно, при оценке СКО 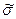используют выражение для СКО 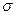, справедливое для достаточно больших п:

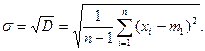(1.1)

Для оценки рассеяния отдельных результатов измерения 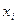от­носительно среднего арифметического значения 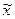определяют оценку СКО этого среднего арифметического

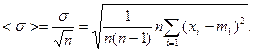(1.2)

Формулы (1.1) и (1.2) связаны простым соотношением

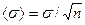(1.3)

Интервальные оценки законов распределения результатов наблюдений. Достоверность любого измерения зависит от степени доверия к его результату и характеризуется веро­ятностью того, что истинное значение измеряемой величины лежит в указанных границах или интервале действительного значения.

Принимая точечную оценку 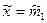за истинное значение изме­ряемой величины, надо убедиться в ее точности. В качестве меры точ­ности рассматривают симметричный интервал 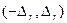в котором с заданной вероятностью Р_Д = 1- q (q - уровень значимо­сти ошибки) располагается ошибка оценки

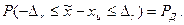
Это выражение принято записывать в следующем виде:

(1.4)

означающим, что истинное значение измеряемой величины с вероят­ностью P_Д попадает в интервал 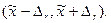В формуле (1.4) интервал 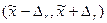шириной 2 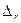и вероятность Р_Д - дове­рительные, а уровень значимости ошибки 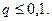. Отметим также, что 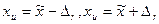называют нижней и верхней границами довери­тельного интервала, а 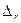- доверительной границей случайной погрешности результата измерения.

Оценку случайных погрешностей с помощью доверительного ин­тервала называют интервальной, а доверительный интервал определя­ют с использованием квантильных оценок погрешностей.

Квантильные оценки распределения случайных погрешностей. Поясним квантильные оценки с помощью графика нормального за­кона распределения случайных погрешности 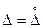(рис.1.1). При таких оценках исходят из того, что площадь, заключенная под кривой плотности распределения погрешностей, отражает вероятность всех возможных значений погрешности и по условиям нормирования рав­на единице. Эту площадь можно разделить вертикальными линиями на части. Абсциссы этих линий называют квантилями.

Под 100Р%-ным (здесь Р - вероятность) квантилем 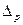понима­ют абсциссу вертикальной линии, слева от которой площадь под кри­вой плотности распределения 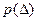равна Р %. Иначе говоря, квантиль - это значение случайной погрешности с заданной доверительной вероятностью Р. На рис.1.1 абсцисса 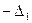есть 25%-ная квантиль, так как площадь под кривой 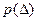слева от нее составляет 25 % всей пло­щади. Абсцисса 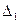соответствует 75%-ной квантили. На практике 25%- и 75%-ный квантили при­нято называть сгибами, или квантилями распределения. Ме­жду ними заключено 50 % всех возможных значений случайной погрешности измерений. 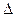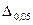Интер­вал значений случайной погреш­ности между и 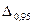охва­тывает 90 % всех возможных значений и называется интер­квантильным промежутком с 90- %-ной вероятностью.

Рис.1.1. Квантильные оценки случайной погрешности

Оценка результата измерения и его СКО. Для удобства анализа результатов и погрешностей измерений предположим, что при выпол­нении п многократных наблюдений одной и той же величины х_и пос­тоянная систематическая погрешность полностью исключена Тогда результат i-гo наблюдения находят с некоторой абсолютной слу­чайной погрешностью .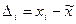

Оценку СКО ряда наблюдений определяют по формуле (3.16) (см. лекцию3):

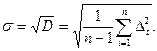(1.5)

Затем вычисляют оценку СКО результата измерения 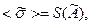которая характеризует степень разброса значений 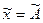по отношению к истинному значению х_и для различных п:

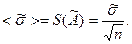(1.6)

Рассмотрим случай измерений с многократными наблюдениями, когда результат i -го наблюдения содержит и случайную и постоянную систематическую погрешности: 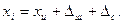Подстановка зна­чений x_i в формулу (3.7) (см. лекцию3) позволяет получить оценку результата из­мерений

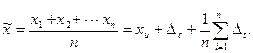(1.7)

Критерий оценки нормальности закона распре­деления при известном СКО. При исключении грубых по­грешностей из результатов наблюдений по этому критерию прово­дят следующие операции:

1. Результаты группы из п наблюдений (объем выборки) упорядо­чивают по возрастанию По формулам (3.7) (см.лекцию 3) и (1.6) вычисляют оценки среднего арифметического значения 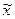и СКО наблюдений 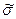этой выборки. Для предполагаемых промаховпроводят расчет коэффициентов:

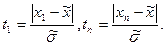(1.8)

2. Задаются уровнем значимости критерия ошибки q. Очевидно, что этот уровень должен быть достаточно малым, чтобы вероят­ность ошибки была невелика. Из таблицы предельных значений коэффициента 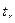по заданному параметру q и числу наблюдений п находят предельное (граничное) значение коэффициента:

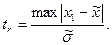(1.9)

3. Сравнивают коэффициенты, определяемые по формулам (1.8) и (1.9). Если выполняются условия 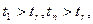то значения х₁ и х_n относят к промахам и исключают из результатов наблюдений.

Критерий «трех сигм». При использовании этого крите­рия устанавливают границы цензурирования 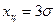. Чаще всего критерий применяют для результатов измерений, распределенных по нормальному закону, и одним из граничных параметров при этом служит оценка СКО измерений. Считается, что результат измерения, полученный с уровнем значимости ошибки q 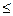0, 003, маловероятен и его относят к грубым погрешностям, если 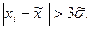Оценк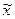и и 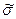вычисляют без учета экстремальных значений величин Х_i. 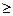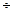Данный критерий хоро­шо работает при числе измерений п 20 50.

Доверительные границы случайной погрешности. При измерениях интерес представляет определение доверuтельно­го uнтервала 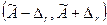, в котором с заданной доверительной ве­роятностью Р_Д находится измеряемая величина 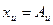. Доверительную вероятность запишем как

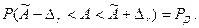
При нормальном законе распределения поиск доверительной границы 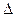,. выполняется с помощью интеграла вероятностей 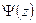. Задают­ся доверительной вероятностью Р_Д и по известной таблице (см. лекцию 3) находят z, соответст­вующее 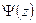= Р_Д. Учитывая z и оценку СКО результата измерений 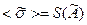определяют доверительную границу случайной погрешности

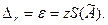(1.10)

Аналитически нижнюю Ан и верхнюю Ав границы дове­рительного интервала представляют в следующем виде:

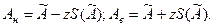
Тогда по заданной доверительной вероятности Р д и числу наблюдений п находят коэффициент Стьюдента t(Р_Д, п). Далее определяют дове­рительную границу случайной погрешности результата измерения

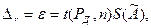(1.11)

а также границы доверительного интервала:

(1.12)

Границы неисключенных систематических погрешностей результата измерения. Неисключенные систематические погрешности принято рассматривать как случайные с равномерным симметричным законом распределения плотности вероятности и определять каждую грани­цу 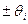, причем в качестве границы 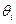принимают, например, пре­делы допускаемых основных и дополнительных погрешностей средств измерений.

Общую границу 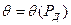числа r НСП вычисляют по формуле

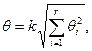(1.13)

где k - коэффициент, зависящий от r, принятой доверительной ве­роятности Р д и связи между составляющими погрешностей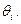

Основная литература: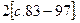

Дополнительная литература: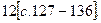

Контрольные вопросы:

1. Что такое доверительная вероятность и доверительный интервал?

2. Что такое интервальная оценка закона распределения?

3. Когда используют квантильные оценки случайных погрешностей?