
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ЛЕКЦИЯ № 12.
|
|
Модели массового обслуживания
Теория массового обслуживания – область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные акты повторяются многократно (предприятия бытового обслуживания; системы приема, переработки и передачи информации; автоматические линии производства и т.п.). Основные элементы таких систем представлены на рис.4.1.
 |
Рис.4.1. Основные элементы системы массового обслуживания
Для повышения уровня организации и качества функционирования систем массового обслуживания (СМО) необходимо прежде всего изучить динамику протекания процессов этих систем с точки зрения воздействия случайных факторов.
Предмет теории массового обслуживания – установление зависимостей между характером потока заявок, числом каналов обслуживания, производительностью отдельного канала и эффективноcтью обслуживания с целью нахождения наилучших путей управления этими процессами.
Задачи теории массового обслуживания в конечном итоге носят оптимизационный характер, включают экономический аспект – определить вариант системы, при котором будет обеспечена минимизация суммарных затрат от ожидания обслуживания (потерь времени и ресурсов на обслуживание) и от простоев каналов обслуживания.
Переходы системы из состояния в состояние можно рассматривать как происходящие под влиянием некоторых потоков событий.
Поток событий называется регулярным, если события следуют одно за другим через строго определенные промежутки времени.
Поток событий называется стационарным, если вероятность появления того или иного числа событий на участке времени длиной 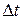 зависит только от длины участка и не зависит от того, где именно на оси
зависит только от длины участка и не зависит от того, где именно на оси  расположен этот участок. Если обозначить
расположен этот участок. Если обозначить 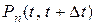 вероятность появления
вероятность появления 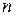 требований (заявок, событий) в промежуток времени
требований (заявок, событий) в промежуток времени 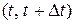 , то свойство стационарности можно записать так:
, то свойство стационарности можно записать так: 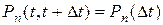 . Стационарность потока соответствует неизменности условий, постоянству работы системы. В этом случае плотность (интенсивность) потока (среднее число требований в единицу времени) постоянна:
. Стационарность потока соответствует неизменности условий, постоянству работы системы. В этом случае плотность (интенсивность) потока (среднее число требований в единицу времени) постоянна: 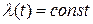 .
.
Поток событий называется потоком без последействия, если вероятность появления на любом участке времени того или иного числа событий не зависит от того, какое число событий попало на другие участки, не пересекающиеся с данным. Это свойство состоит в том, что вероятность 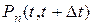 не зависит от порядка и интенсивности поступления требований до момента
не зависит от порядка и интенсивности поступления требований до момента  , т.е. в таком потоке текущие требования поступают в систему независимо от предшествующих.
, т.е. в таком потоке текущие требования поступают в систему независимо от предшествующих.
Поток событий называется ординарным, если вероятность попадания на элементарный участок 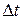 двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Это свойство состоит в том, что практически невозможно одновременное поступление на обслуживание двух или более требований. Если обозначить
двух или более событий пренебрежимо мала по сравнению с вероятностью попадания одного события. Это свойство состоит в том, что практически невозможно одновременное поступление на обслуживание двух или более требований. Если обозначить 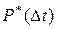 вероятность поступления в систему за время
вероятность поступления в систему за время 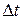 более одного требования, то это свойство можно выразить следующим образом:
более одного требования, то это свойство можно выразить следующим образом: 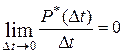 .
.
Ординарный поток без последействия называется пуассоновским. Если события образуют пуассоновский поток, то число событий 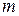 , падающих на любой участок времени
, падающих на любой участок времени 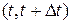 , распределено по закону Пуассона:
, распределено по закону Пуассона: 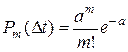 , где
, где 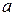 – математическое ожидание числа точек, попадающих на участок
– математическое ожидание числа точек, попадающих на участок 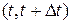 :
: 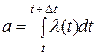 .
.
Если плотность потока 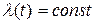 , то пуассоновский поток называется “стационарным пуассоновским” или простейшим потоком.
, то пуассоновский поток называется “стационарным пуассоновским” или простейшим потоком.
В марковском случайном процессе все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими.
Для простейшего потока число событий, попадающих на любой участок длины 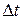 , распределено по закону Пуассона с параметром
, распределено по закону Пуассона с параметром 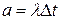 .
.
Расстояние 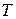 между двумя соседними событиями в простейшем потоке есть непрерывная случайная величина, распределенная по показательному закону с плотностью
между двумя соседними событиями в простейшем потоке есть непрерывная случайная величина, распределенная по показательному закону с плотностью 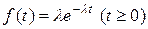 и параметрами
и параметрами 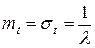 .
.
При суммировании (взаимном наложении) большого числа ординарных стационарных потоков (при условии, что складываемые потоки оказывают на сумму приблизительно равномерно малое влияние) с практически любым последействием получается поток, сколь угодно близкий к простейшему.
Если промежуток времени 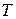 распределен по показательному закону, то любые сведения о том, сколько времени уже длился этот промежуток, не влияют на закон распределения оставшегося времени. Показательный закон – единственный, обладающий таким свойством.
распределен по показательному закону, то любые сведения о том, сколько времени уже длился этот промежуток, не влияют на закон распределения оставшегося времени. Показательный закон – единственный, обладающий таким свойством.
Если поток событий нестационарен, то его основной характеристикой является мгновенная плотность 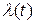 , являющаяся пределом отношения среднего числа событий, приходящегося на элементарный участок времени
, являющаяся пределом отношения среднего числа событий, приходящегося на элементарный участок времени 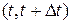 , к длине этого участка, когда последняя стремится к нулю:
, к длине этого участка, когда последняя стремится к нулю:
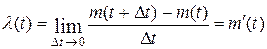 ,
,
где 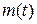 – математическое ожидание числа событий на участке
– математическое ожидание числа событий на участке 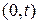 .
.
Ординарный поток однородных событий называется потоком с ограниченным последействием (или потоком Пальма), если промежутки времени между последовательностями событий 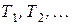 представляют собой независимые случайные величины. Очевидно, простейший поток является частным случаем потока Пальма, в нем расстояния
представляют собой независимые случайные величины. Очевидно, простейший поток является частным случаем потока Пальма, в нем расстояния 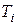 представляют собой независимые случайные величины, распределенные по показательному закону. Нестационарный пуассоновский поток не является потоком Пальма.
представляют собой независимые случайные величины, распределенные по показательному закону. Нестационарный пуассоновский поток не является потоком Пальма.
Для нестационарного потока (ординарного, без последействия, с переменной плотностью 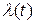 ) закон распределения промежутка времени
) закон распределения промежутка времени 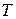 между соседними событиями выражается плотностью распределения в виде
между соседними событиями выражается плотностью распределения в виде
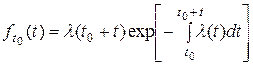
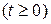 .
.
Потоком Эрланга 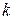 -го порядка называется поток, получаемый из простейшего путем “разрежения”, т.е. если сохранить каждую
-го порядка называется поток, получаемый из простейшего путем “разрежения”, т.е. если сохранить каждую 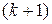 -ю точку, а остальные удалить. Очевидно, простейший поток можно рассматривать как поток Эрланга нулевого порядка.
-ю точку, а остальные удалить. Очевидно, простейший поток можно рассматривать как поток Эрланга нулевого порядка.
При увеличении порядка 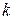
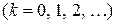 (и одновременном уменьшении масштаба по оси
(и одновременном уменьшении масштаба по оси  , делением на
, делением на 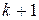 ) поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными
) поток Эрланга приближается к регулярному потоку с постоянными интервалами, равными 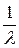 .
.
Если 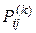 – вероятность перехода системы из состояния
– вероятность перехода системы из состояния 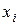 в состояние
в состояние 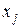 на
на 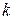 -м шаге, то вероятность того, что система
-м шаге, то вероятность того, что система 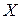 будет находиться после
будет находиться после 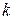 шагов в состоянии
шагов в состоянии 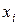 выражается формулой:
выражается формулой:
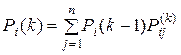 ;
; 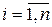 .
.
Классификацию широкого разнообразия СМО можно провести по различным признакам (табл.4.1).
Системы массового обслуживания с ожиданием бывают разомкнутые и замкнутые. Разомкнутая (открытая) система – это система с неограниченным источником потока требований (например, покупатели в магазинах, пассажиры в метро и т.д.).
Замкнутая – это система, в которой поток требований ограничен. Замкнутые системы обслуживают конечное число требований. Как только требования обслужены, они возвращаются в источник (рис.4.2).
Задачи такого типа часто встречаются при эксплуатации машин (оборудования), когда отремонтированные машины возвращаются в цех и становятся источником новых требований.
|
|
|
 |  |  | |||||
 | |||||||
|
|