
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Расчет коэффициентов множественной линейной регрессии
|
|
Для того чтобы формально можно было решить задачу, то есть найти некоторый наилучший вектор параметров, должно быть N ≥ т+ 1 (N -количество наблюдений, m -количество факторов). Если это условие не выполняется, то можно найти бесконечно
много разных векторов коэффициентов, при которых линейная формула абсолютно точно связывает между собой x и y. Так, две точки в трехмерном пространстве определяют одну прямую, через которую можно провести целый пучок плоскостей.
Но через три точки, если они не лежат на одной прямой, в трехмерном пространстве можно провести только одну плоскость. Если число данных больше минимально необходимого, то есть N > т+ 1, то, как правило, нельзя подобрать линейную формулу, в точности удовлетворяющую всем наблюдениям, и возникает необходимость оптимизации, то есть выбора наилучшего приближения для имеющихся данных. Положительная разность (N-m- 1)в этом случае называется числом степеней свободы.
Если число степеней свободы мало, то статистическая надежность оцениваемой формулы невысока. Так, если проведена плоскость " в точности" через имеющиеся три точки наблюдений, любая четвертая точка из той же генеральной совокупности будет практически наверняка лежать вне этой плоскости. Обычно при оценке множественной регрессии для обеспечения статистической надежности требуется, чтобы число наблюдений, по крайней мере, в 3 раза превосходило число оцениваемых параметров.
Задача построения множественной линейной регрессии состоит в нахождении (m +1) – мерного вектора a = (a, a 1,..., a m), минимизирующего (согласно выбранному критерию) погрешность прогноза. Критерии возможны различные, но обычно используется метод наименьших квадратов (МНК).
Тогда связь между одной зависимой переменной (y) и несколькими независимыми переменными (x) будет выражена линейным уравнением:
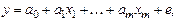
где Y – зависимая переменная; х 1,..., х m – независимые переменные; a, a 1,..., a m – параметры модели; e – ошибка. Критерием для нахождения вектора a является:
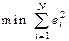 .
.
Проблема здесь состоит не только в том, чтобы объяснить возможно большую долю колебаний переменной Y, но и отделить влияние каждого из факторов, рассматриваемых как объясняющие переменные.
Минимизируемое выражение является квадратичной функцией относительно неизвестных величин b, b 1,..., b m. Необходимым условием ее минимума является равенство нулю всех ее частных производных. Частные производные квадратичной функции являются линейными функциями, и, приравнивая их всех к нулю, мы получим систему из (т+ 1 ) линейных уравнений с (m +1) неизвестными. Такая система имеет обычно единственное решение за исключением особого случая, когда ее столбцы линейно зависимы и решения нет или их бесконечно много. Однако данные реальных статистических наблюдений к такой ситуации, как правило, никогда не приводят. Полученная система называется системой нормальных уравнений. Ее решение, по сути, является обобщением случая парной регрессии. Вычисление коэффициентов регрессии (включая свободный член) производится так, чтобы минимизировать среднеквадратическую ошибку для всей совокупности имеющихся наблюдений и реализуется как решение системы линейных уравнений.
|
|