Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Алгебраические критерии устойчивости
|
|
3.2.1 Необходимое условие устойчивости
Необходимым условием устойчивости линейной непрерывной АС является положительность всех коэффициентов характеристического уравнения, т.е.
a1> 0, a2> 0, …, an-1> 0, an> 0, если а0> 0.
В случае отрицательности всех коэффициентов, то есть при аi < 0, можно поменять знаки всех коэффициентов на обратные.
Однако в общем случае положительность коэффициентов характеристического уравнения не является достаточной для устойчивости системы. Можно доказать, что только для линейных непрерывных АС первого и второго порядков необходимое условие устойчивости является и достаточным.
У устойчивой линейной дискретной АС коэффициенты ХП могут иметь разные знаки.
3.2.2 Критерий Гурвица
Для оценки устойчивости критерием Гурвица из коэффициентов характеристического уравнения A(l) = aоln+a1ln-1+¼ +an-1l+an = формируют матрицу Гурвица Dn по следующему правилу: по главно 
й диагонали слева направо выписывают все коэффициенты от a1 до an в порядке возрастания индексов. Остальные элементы определителя Δ n заполняются по столбцам. Вверх от главной диагонали размещаются коэффициенты с последовательно возрастающими индексами до коэффициента an, а вниз от нее – коэффициенты с последовательно убывающими индексами до коэффициента a0. Оставшиеся места определителя заполняются нулями.
Для устойчивости линейной непрерывной АС необходимо и достаточно, чтобы все определители Гурвица (то есть диагональные миноры Di) имели знаки, одинаковые со знаком aо, т.е. при aо > 0 были положительными:
D1 = a 1 > 0, D2 =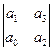 
> 0, D3 = 
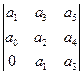> 0, …, Dn > 0.
Обычно критерий Гурвица используется при n ≤ 4.
Для линейной дискретной АС алгебраические условия устойчивости гораздо сложнее. Пусть её ХП имеет вид
.
В аналитическом виде условия устойчивости для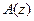 
первых четырех порядков выглядят следующим образом:
- полином первого порядка a1 z+a0=0;
a1+a0> 0; a1-a0> 0;
- полином второго порядка a2 z2+a1 z+a0=0;
a2+a1+a0> 0; a2-a1+a0> 0; a2-a0> 0;
- полином третьего порядка a3 z3+a2 z2+a1 z+a0=0;
a3+a2+a1+a0> 0; a3-a2+a1-a0> 0;
a3(a3-a1)-a0(a0-a2)> 0; 3(a3+a0)-a2-a0> 0;
- полином четвёртого порядка a4 z4+a3 z3+a2 z2+a1 z+a0=0;
a4+a3+a2+a1+a0> 0; a4-a3+a2-a1+a0> 0;
(a4-a0)[a3(a1-a3)-(a2-a4-a0)(a4-a0)]+a4(a1-a3)2> 0;
2(а4-a0)+(a1-a3)> 0;
2(а4-a0)+(a3-a1)> 0.
|
|