Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
На дом № 2868, 2878, 2880, 2882, 2884, 2886, 2903, 2906, 2914, 2922, 2924, 2931, 2935.
|
|
Рассмотрим соотношение коэффициентов степенного ряда
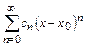
и многочлена Тейлора функции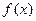 
в окрестности точки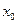 
.
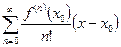В соответствии с утверждением теоремы 12.2 степенной ряд в области его сходимости 
можно почленно дифференцировать любое число раз, т.е.
, 
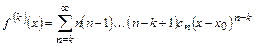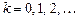(13.1)
Полагая в (13.1)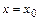 
, получим
, 
, 
,
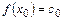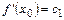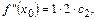
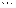
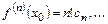откуда следует
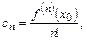
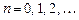(13.2)
Эти выражения для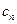 
называются коэффициентами Тейлора функции 
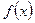в точке 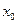. Формально составленный ряд с этими коэффициентами
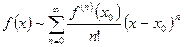(13.3)
называется рядом Тейлора функции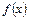 
по степеням 
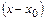или рядом Маклорена в случае 
.
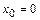Рассмотрение вопроса о том, когда в формуле (13.3) вместо знака соответствия можно поставить знак равенства, мы вынуждены отложить. Будем считать, что функция 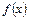может быть представлена своим рядом Тейлора или Маклорена в области сходимости ряда.
Получим разложения некоторых функций по степеням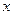 
, находя коэффициенты по формуле (13.2).
1. 
, 
,
(
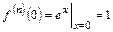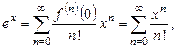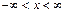) (13.4)
Определим радиус сходимости полученного ряда:
,
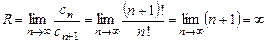следовательно, ряд (13.4) сходится на всей числовой оси при .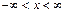
2. 
.
, 
,
, 
,
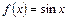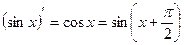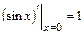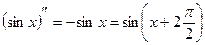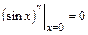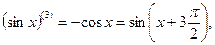
и т.д.
Очевидно, что 
, 
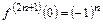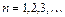, следовательно
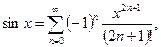
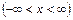. (13.5)
Определим радиус сходимости ряда
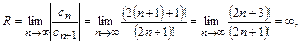
следовательно, ряд (13.5) сходится на всей числовой оси.
3. 
.
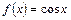Почленным дифференцированием ряда (13.5) получим:
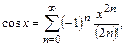
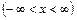. (13.6)
4. 
.
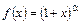В случае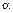 
целого положительного это бином Ньютона и в разложении содержится конечное число членов. Если же 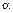отлично от целого числа, то производные имеют вид
,
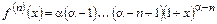откуда следует, что
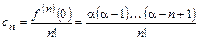для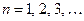 
.
Получаемый ряд называется биномиальным:
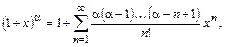
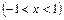. (13.7)
Определим радиус сходимости полученного ряда:
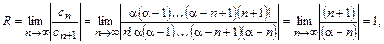
следовательно, ряд сходится на интервале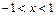 
.
Ряд для функции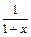 
есть частный случай биномиального ряда при 
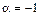и может быть получен из (13.7) подстановкой :
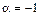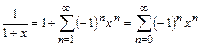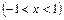, , (13.8)
Ряд для функции 
легко получить из предыдущего выражения:
, 
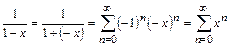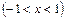. (13.9)
Используя возможность почленного интегрирования степенных рядов (теорема 12.3), найдем разложения для функци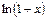й 
и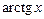 
.
.
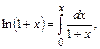
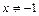Подставим в этот интеграл ряд (13.8), получим:
.
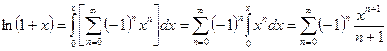Таким образом,
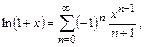
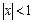. (13.10)
Разложение для 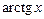будем искать, исходя из соотношения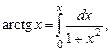 
в которое подставим ряд
.
В результате почленного интегрирования получаем:
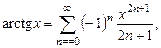
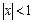. (13.11)
Непосредственное вычисление коэффициентов Тейлора по формулам (13.2) часто приводит к громоздким выкладкам, поэтому представляют интерес искусственные приёмы разложения функций в ряды с использованием формул (13.4) – (13.11), которые позволяют существенно упростить дело.
Пример 13.1. Разложить в ряд Маклорена функцию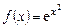 
.
Решение. По формуле (13.4)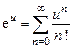 
. Пусть 
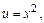тогда при 
будет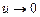 
и формулу (13.4) можно использовать. Получаем:
.
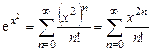Пример 13.2. Разложить по степеням 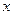функцию 
.
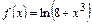Решение. Воспользуемся разложением (13.10):
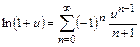, полагая 
,
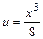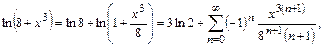
Условие сходимости ряда: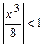 
или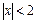 
.
Пример 13.3. Разложить в ряд Маклорена функцию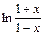 
.
Решение. Поскольку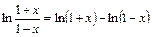 
, запишем
,
.
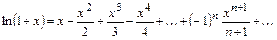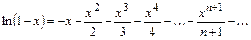Вычитая из первого равенства второе, получим:
.
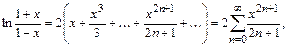
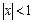Пример 13.4. Получить ряд Маклорена для интегрального синуса
.
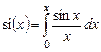Решение. Воспользуемся разложением (13.5) и проинтегрируем ряд почленно:
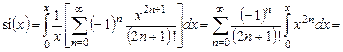
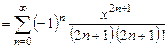
Контрольные вопросы.
- Запишите ряда Тейлора функции .
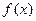- Что называется рядом Маклорена функции ?
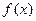- Выпишите разложения в ряд Маклорена основных элементарных функций.
|
|