
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Диференціююча ланка
|
|
Диференціюючою називають таку ланку, в якій вихідна величина пропорційна похідній від вхідної величини
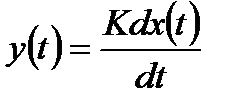 . (3.48)
. (3.48)
Перетворимо рівняння (3.48) за Лапласом
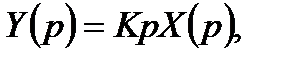 тоді
тоді 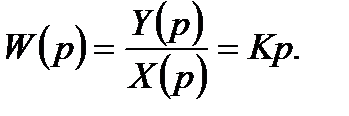
Знаходимо перехідну функцію ланки, перехідна характеристика якої показана на рис. 3.10
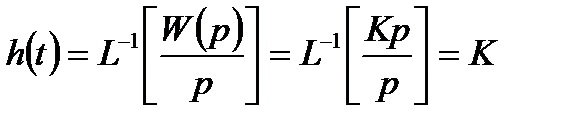 .
.
Амплітудно-фазова функція
 .
.
АФХ співпадає з уявною віссю (рис. 3.11).
АЧХ: 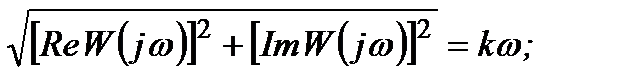
ФЧХ: 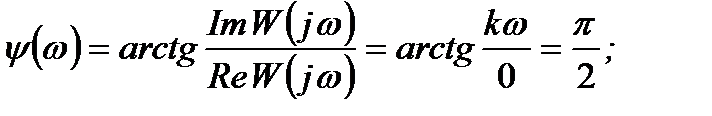
ЛАЧХ: 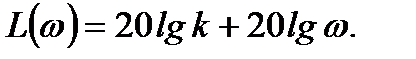
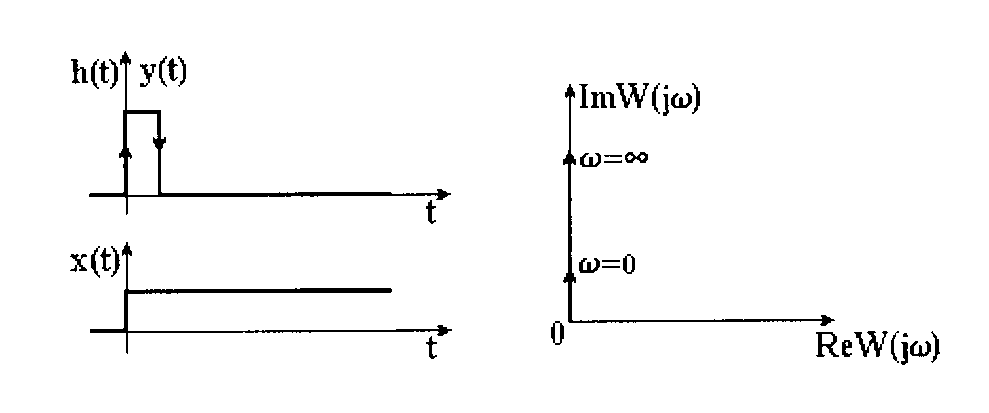
| Рисунок 3.10 – Перехідна характеристика диференціюючої ланки | Рисунок 3.11 – АФХ диференціюючої ланки |
Реальна диференціююча ланка являє собою послідовне з’єднання ідеальної диференціюючої ланки та інерційної ланки І-го порядку. Вона має таке диференціальне рівняння:
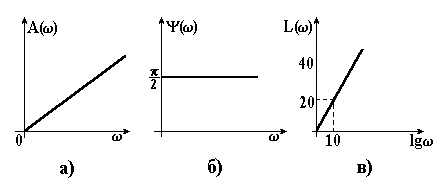 Рисунок 3.12 – АЧХ (а), ФЧХ (б), ЛАЧХ (в) диференціюючої ланки
Рисунок 3.12 – АЧХ (а), ФЧХ (б), ЛАЧХ (в) диференціюючої ланки
|
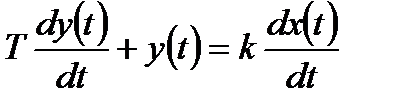 (3.49)
(3.49)
і передавальну функцію
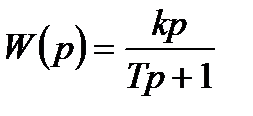 . (3.50)
. (3.50)
Таку ланку можна зобразити у вигляді послідовного або паралельного з’єднання безінерційної і інерційної ланок (рис. 3.13).
Характеристики реальної диференціюючої ланки приведені на рисунку 3.14.
Приклади реальних диференціюючих ланок приведені на рисунку 3.15.
Диференціюючі ланки в статичному режимі не передають сигналу на вихід, вони добре пропускають високочастотні сигнали і погано-низькочастотні. Вони вносять додатковий фазовий зсув.
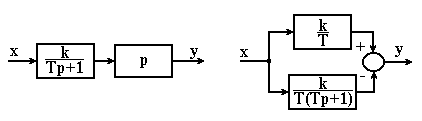 Рисунок 3.13 – Реальні диференціюючі ланки
Рисунок 3.13 – Реальні диференціюючі ланки
|
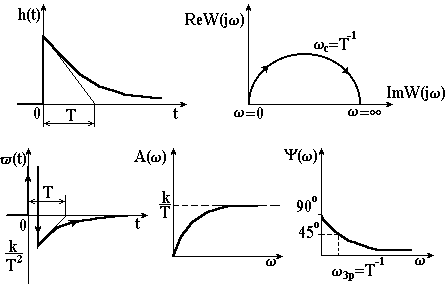 Рисунок 3.14 – Характеристики реальної диференціюючої ланки
Рисунок 3.14 – Характеристики реальної диференціюючої ланки
|
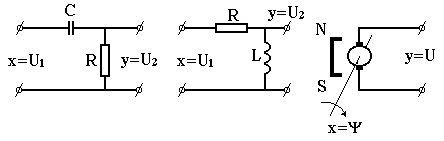 Рисунок 3.15 – Приклади диференціюючих ланок
Рисунок 3.15 – Приклади диференціюючих ланок
|
3.7 Інерційні ланки другого порядку
Диференціальне рівняння ланок ІІ-го порядку має вигляд
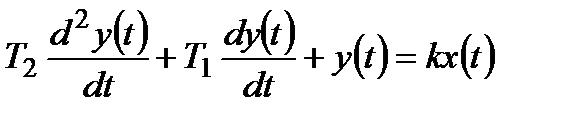 . (3.51)
Йому відповідає рівняння динаміки в операторній формі . (3.51)
Йому відповідає рівняння динаміки в операторній формі
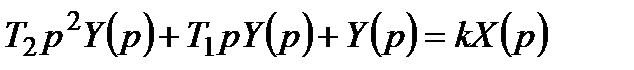 (3.52)
і передавальна функція (3.52)
і передавальна функція
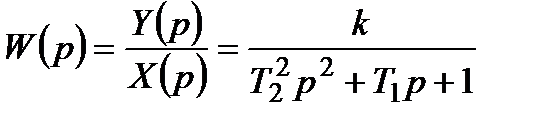 . (3.53)
Характеристичне рівняння . (3.53)
Характеристичне рівняння 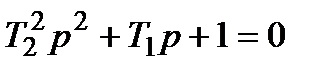 має два корені має два корені
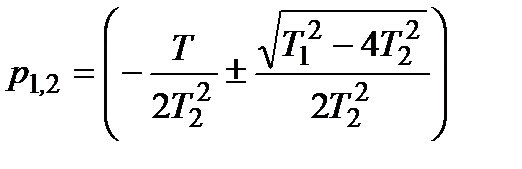 . (3.54)
Характер перехідного процесу залежить від типу коренів, які можуть бути дійсними, комплексними і уявними. . (3.54)
Характер перехідного процесу залежить від типу коренів, які можуть бути дійсними, комплексними і уявними.
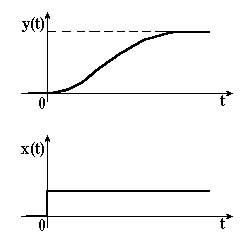 Рисунок 3.16 – Перехідна характеристика аперіодичної ланки ІІ-го порядку
Рисунок 3.16 – Перехідна характеристика аперіодичної ланки ІІ-го порядку
|
І. Якщо 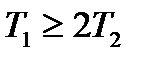 , то обидва корені дійсні, тобто
, то обидва корені дійсні, тобто
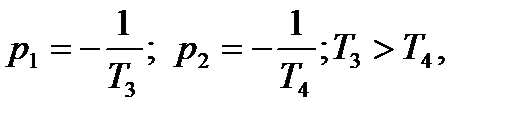
де 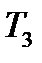 і
і 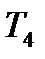 – умовні постійні часу.
– умовні постійні часу.
Перехідна характеристика такої ланки є монотонною. Вона близька до інерційної ланки І-го порядку, тому її називають – аперіодична ланка ІІ-го порядку.
При  передавальну функцію (3.53) можна представити в таких еквівалентних формах:
передавальну функцію (3.53) можна представити в таких еквівалентних формах:
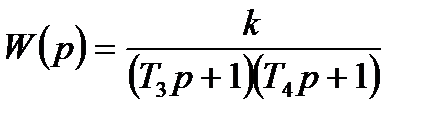 , (3.55)
, (3.55)
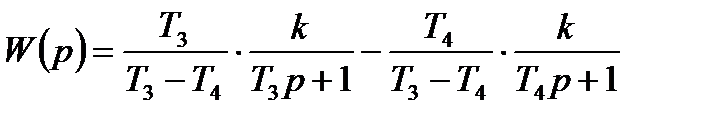 , (3.56)
, (3.56)
яким відповідають алгоритмічні схеми, приведені на рисунку 3.17, б, г.
ІІ. Якщо 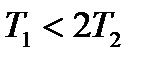 , то корені характеристичного рівняння комплексні і спряжені
, то корені характеристичного рівняння комплексні і спряжені
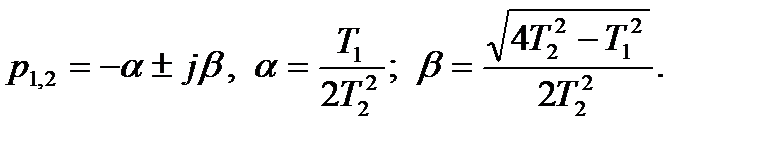 (3.57)
(3.57)
Перехідна характеристика в цьому випадку носить коливальний характер (рис. 3.18). Тобто, маємо коливальну ланку.
ІІІ. Якщо 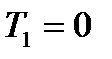 , то обидва корені уявні, і перехідна характеристика являє собою незатухаючу синусоїду. Інерційну ланку ІІ-го порядку з
, то обидва корені уявні, і перехідна характеристика являє собою незатухаючу синусоїду. Інерційну ланку ІІ-го порядку з 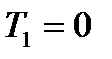 називають ідеальною коливальною або консервативною.
називають ідеальною коливальною або консервативною.
Поряд із загальними властивостями всі ланки реально відрізняються одна від одної. Розглянемо окремо характеристики інерційних ланок ІІ-го порядку.
Перехідна функція аперіодичної ланки ІІ-го порядку може бути одержана додаванням загального рішення
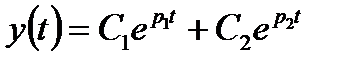 (3.58)
(3.58)
і рішення, яке відповідає примусовій складовій при 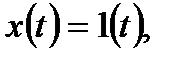 тоді перехідна функція має такий вигляд:
тоді перехідна функція має такий вигляд:
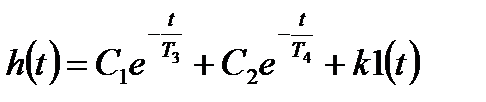 . (3.59)
. (3.59)
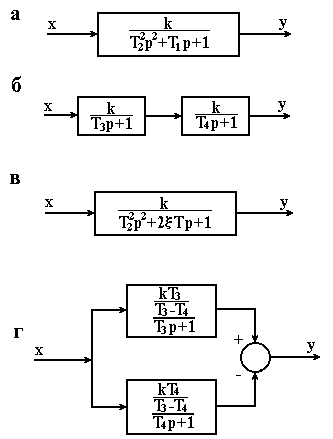 Рисунок 3.17 – Алгоритмічні схеми інерційних ланок ІІ-го порядку
Рисунок 3.17 – Алгоритмічні схеми інерційних ланок ІІ-го порядку
|
Після підстановки початкових умов 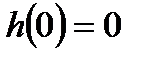 і
і  у вираз (3.59), маємо
у вираз (3.59), маємо
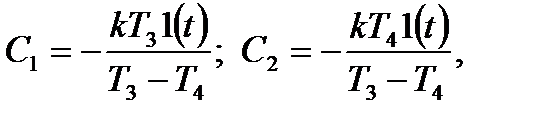 (3.60)
(3.60)
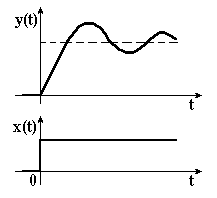
| 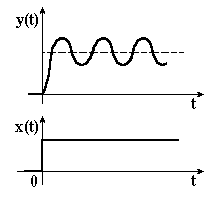
|
| Рисунок 3.18 – Перехідна характеристика коливальної ланки | Рисунок 3.19 – Перехідна характеристика консервативної ланки |
тоді перехідна функція має такий вигляд:
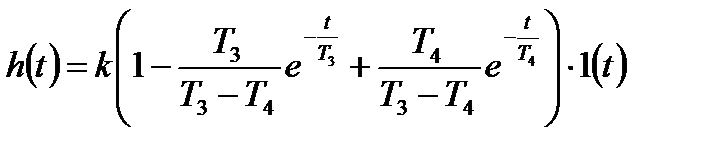 . (3.61)
. (3.61)
Передавальна функція
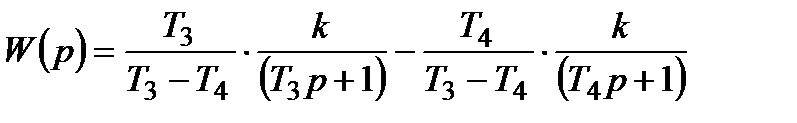 . (3.62)
. (3.62)
Сталі часу 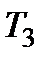 і
і 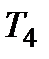 можна визначити на підставі графікоекспериментальної перехідної характеристики.
можна визначити на підставі графікоекспериментальної перехідної характеристики.
Характеристики аперіодичної ланки ІІ-го порядку показані на рис 3.21.
З частотних характеристик даної ланки випливає, що вона добре пропускає сигнали низької частоти і погано пропускає сигнали високої частоти.
Коливальна ланка – це така ланка, в якій при стрибкоподібній зміні вхідної величини вихідна величина прямує до нового встановленого значення, здійснюючи навколо нього затухаючі коливання.
Для більш детального вивчення диференціальне рівняння ланки записують у такому вигляді:
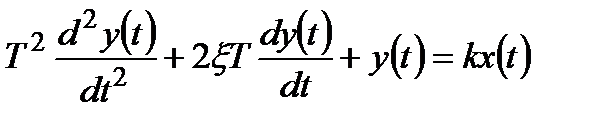 , (3.63)
, (3.63)
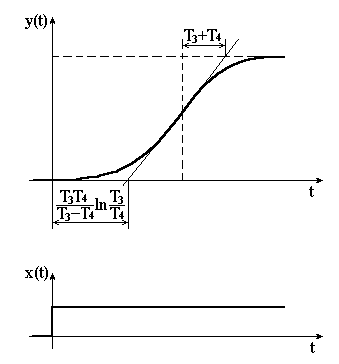 Рисунок 3.20 – Перехідна характеристика аперіодичної ланки ІІ-го порядку
Рисунок 3.20 – Перехідна характеристика аперіодичної ланки ІІ-го порядку
|
де 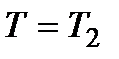 – постійна часу, яка характеризує інерційність ланки;
– постійна часу, яка характеризує інерційність ланки; 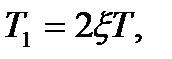 де
де 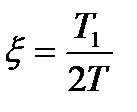 – відносний коефіцієнт затухання; він характеризує коливальність ланки і змінюється від 0 до 1.
– відносний коефіцієнт затухання; він характеризує коливальність ланки і змінюється від 0 до 1.
Перетворивши рівняння (3.63) за Лапласом, отримаємо передавальну функцію
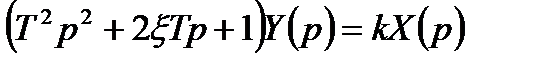 , (3.64)
, (3.64)
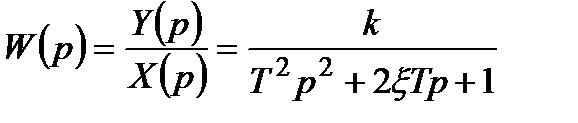 . (3.65)
. (3.65)
Ця передавальна функція вигідніша, бо тут фігурує одна постійна часу Т. Прирівнюючи до нуля знаменник (3.65), одержимо характеристичне рівняння
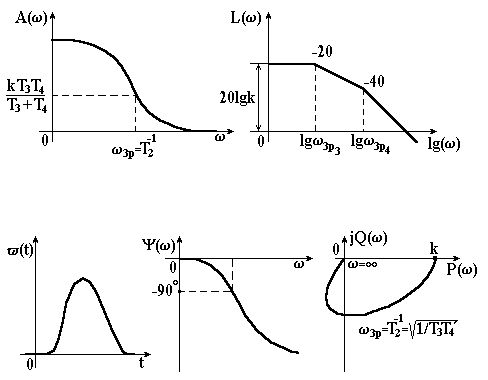 Рисунок 3.21 – Характеристики аперіодичної ланки ІІ-го порядку
Рисунок 3.21 – Характеристики аперіодичної ланки ІІ-го порядку
|
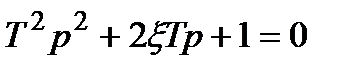 . (3.66)
. (3.66)
Розв’язуючи це рівняння відносно р, будемо мати
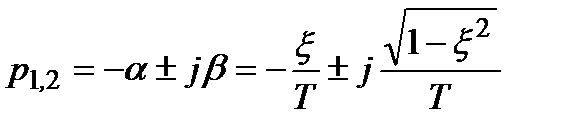 , (3.67)
, (3.67)
де 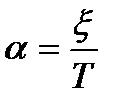 – коефіцієнт затухання;
– коефіцієнт затухання; 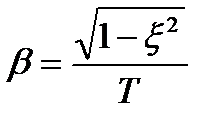 – кутова частота затухання коливань, рад/с.
– кутова частота затухання коливань, рад/с.
Підставляючи в загальний розв’язок диференціального рівняння (3.58) значення комплексних коренів (3.67) і додавши до нього часткове рішення 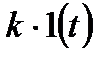 , отримаємо перехідну функцію коливальної ланки
, отримаємо перехідну функцію коливальної ланки
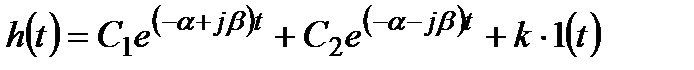 , (3.68)
, (3.68)
За допомогою формули Ейлера
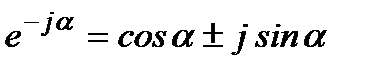 (3.69)
(3.69)
функцію (3.68) можна перетворити до такого вигляду:
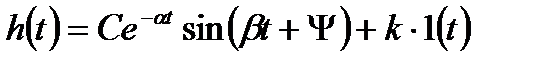 . (3.70)
. (3.70)
Використовуючи початкові умови 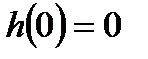 і
і  , знайдемо
, знайдемо
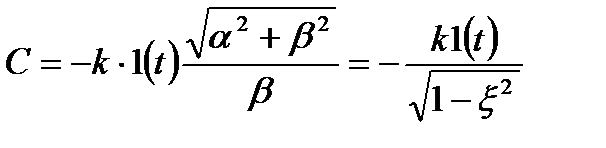 , (3.71)
, (3.71)
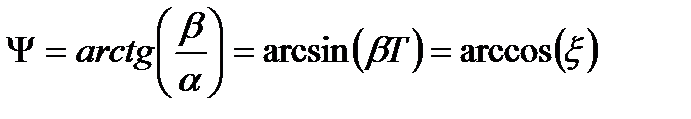 . (3.72)
. (3.72)
Остаточно перехідна функція може бути записана в наступному вигляді:
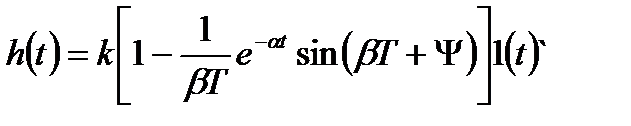 . (3.73)
. (3.73)
Вільна складова перехідної функції (рис. 3.22, а) являє собою синусоїду, амплітуда якої зменшується за законом експоненти.
Період затухаючих коливань дорівнює
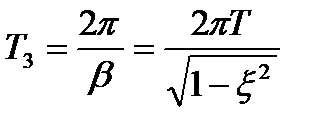 . (3.74)
. (3.74)
Чим менша постійна часу Т і чим більший коефіцієнт демпфування x, тим швидше затухають коливання. Якщо коефіцієнт демпфування 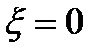 , що відповідає
, що відповідає 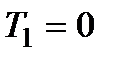 , то на виході ланки після подачі одиничного ступінчатого впливу виникають незатухаючі коливання з частотою
, то на виході ланки після подачі одиничного ступінчатого впливу виникають незатухаючі коливання з частотою 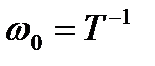 .
.
Швидкість затухання коливального перехідного процесу оцінюють степенем затухання
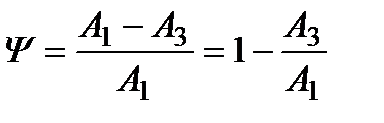 . (3.75)
. (3.75)
Чим ближче до одиниці, тим швидше затухають коливання. Степінь затухання залежить від співвідношення дійсної і уявної частин комплексного кореня. Дійсно, якщо у вираз (3.73) підставити два значення t, які відрізняються на період затухання коливань 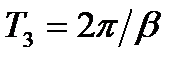 , то можна отримати
, то можна отримати
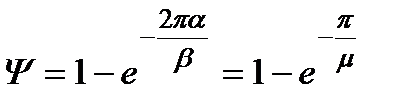 . (3.76)
. (3.76)
Відношення 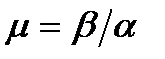 називають ступенем коливальності.
називають ступенем коливальності.
Використовуючи вираз (3.67), можна з’ясувати зв’язок між ступенем коливальності m і коефіцієнтом демпфування x
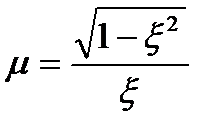 . (3.77)
. (3.77)
Від коефіцієнта x залежить максимальне значення перехідної функції.
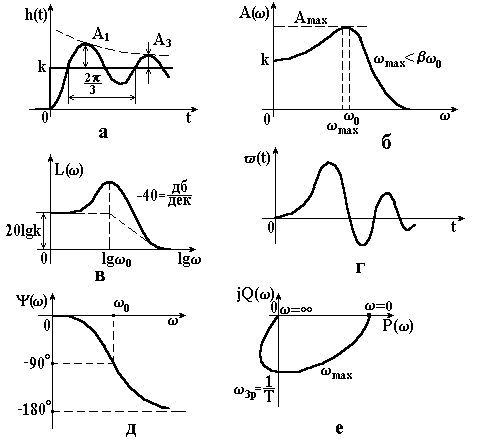 Рисунок 3.22 – Характеристики коливальної ланки ІІ-го порядку
Рисунок 3.22 – Характеристики коливальної ланки ІІ-го порядку
|
Продиференціювавши (3.70) за t і прирівнявши похідну до нуля, одержимо
 , (3.78)
, (3.78)
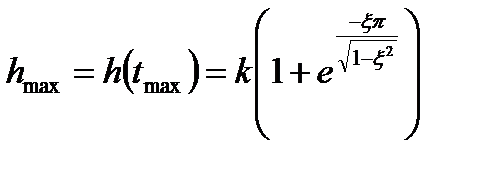 . (3.79)
. (3.79)
АФХ коливальної ланки (рис. 3.22, е) описується функцією
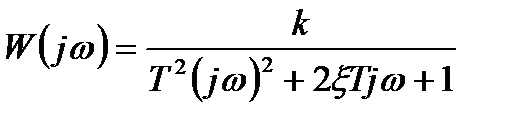 . (3.80)
. (3.80)
3.8 Ланка запізнення
Ланка запізнення – це ланка, вихідна величина якої така сама, як і вхідна, але зсунута на величину чистого запізнення t (рис. 3.23).
Передавальну функцію цієї ланки визначають, користуючись виразами для вхідного і вихідного сигналів, перетворених за Фур’є
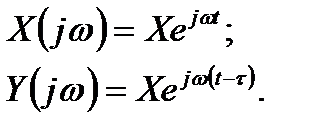
Тоді АФХ

Отже,
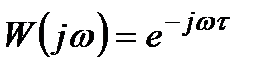 .
.
Запишемо передавальну функцію
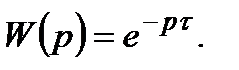
Якщо ланка запізнення має передавальний коефіцієнт, що відрізняється від одиниці, тобто 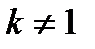 , то
, то
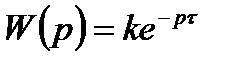 .
.
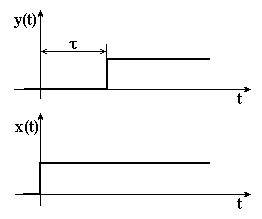 Рисунок 3.23 – Перехідна характеристика ланки запізнення
Рисунок 3.23 – Перехідна характеристика ланки запізнення
|
Взагалі, запізненням володіють такі ланки, які мають різні властивості. Наприклад: 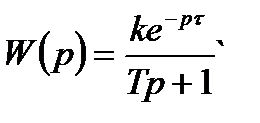 – інерційна ланка І-го порядку.
– інерційна ланка І-го порядку.
Такі ланки представляють у вигляді двох послідовно з’єднаних ланок.
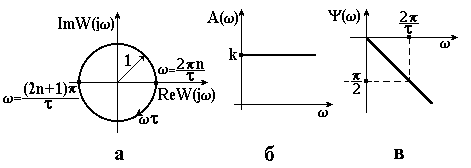 Рисунок 3.24 – АФХ (а), АЧХ (б) і ФЧХ (в) ланки запізнення
Рисунок 3.24 – АФХ (а), АЧХ (б) і ФЧХ (в) ланки запізнення
|
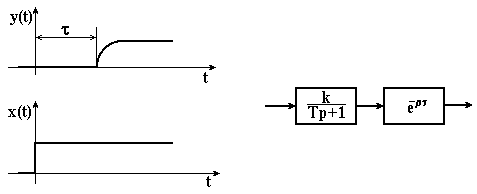 Рисунок 3.25 – Перехідна характеристика інерційної ланки І-го порядку
Рисунок 3.25 – Перехідна характеристика інерційної ланки І-го порядку
|
Найбільш характерним прикладом ланки запізнення є: стрічковий живильник (рис. 3.26, а), що транспортує сипкий матеріал (руду, концентрат). Запізнення t (с) між кількістю матеріалу 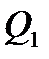 (кг/с), який викидається в одиницю часу на живильник матеріалу
(кг/с), який викидається в одиницю часу на живильник матеріалу 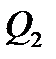 (кг/с) на спуску живильника залежить від довжини L (м) і швидкості руху v (м/с)
(кг/с) на спуску живильника залежить від довжини L (м) і швидкості руху v (м/с)
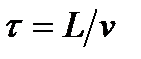 . (3.81)
. (3.81)
Другим розповсюдженим прикладом ланки запізнення є трубопровід (рис. 3.26, б), по якому в технічний об’єкт керування рідка речовина (пульпа, розчин реагенту) в кількості 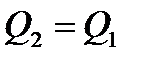 (м3/с) з концентрацією корисного компоненту
(м3/с) з концентрацією корисного компоненту
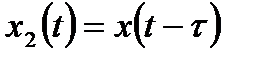 (кг/м3).
(кг/м3).
Зазначимо, що необхідність розглядати живильник, трубопровід та інші транспортуючі пристрої як ланки запізнення виникають лише в тих випадках, коли вони є елементами замкнутих автоматичних систем керування.
Таким чином, ланка запізнення відзначається наступними характерними особливостями:
1. Вона передає будь-які вхідні сигнали без спотворення їх форми, але затримує на інтервалі t в сталому режимі (при 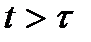 ) вихідний сигнал.
) вихідний сигнал.
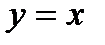 . (3.82)
. (3.82)
Як і для інших статичних (позиційних) ланок, передавальна функція ланки
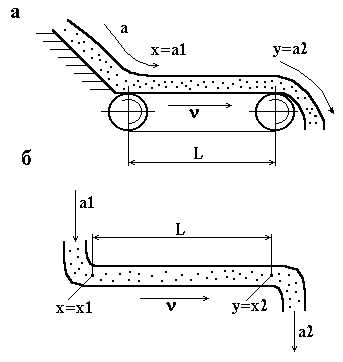 Рисунок 3.26 – Ланки з запізненням
Рисунок 3.26 – Ланки з запізненням
|
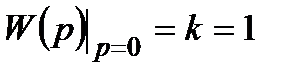 . (3.83)
. (3.83)
2. За властивостями АЧХ ланка запізнення еквівалентна безінерційній: пропускає високочастотні і низькочастотні сигнали з однаковим відношенням амплітуд (рівним одиниці).
3. За властивостями ФЧХ вона еквівалентна інерційним ланкам: створює від’ємний зсув (пропорційний запізненню t і частоті w).
ЛЕКЦІЯ 4
СТІЙКІСТЬ АВТОМАТИЧНИХ СИСТЕМ І ПОКАЗНИКИ ЯКОСТІ ПЕРЕХІДНИХ ПРОЦЕСІВ
4.1 Поняття стійкості автоматичних систем керування
Вияснимо фізичне трактування поняття стійкості. Роглянемо кулю, поміщену у верхню точку підвищення. Вона знаходиться в нестійкому положенні. Дійсно, достатньо найменшого відхилення кулі від початкового положення, як вона скотиться по схилу поверхні і не повернеться у вихідне положення.
Навпаки, куля, що знаходиться у впадині, займає стійке положення, і після відхилення вона обов’язково повернеться до свого початкового положення.
Таким чином, стійкість – це властивість системи (куля – поверхня) повертатись у вихідний стан після виведення її з цього стану та припинення дії збурення.
Як видно з визначення, здатність системи повертатись в початковий стан пов’язується з початковими відхиленнями. В розглянутих прикладах стійкість і нестійкість не залежать від початкових відхилень кулі. Але можна уявити собі таку систему, яка при малому відхиленні повертається, а при великому – не повертається у вихідне положення. Прийнято вважати, що така система стійка в малому і нестійка у великому, оскільки стійкість пов’язана з величиною початкового відхилення. Система, з кулею, що знаходиться у впадині є безмежно стійкою, так як куля буде повертатись у вихідне положення при будь-якому початковому відхиленні. Система має властивості байдужої рівноваги.
Чи завжди за вихідний стан системи, стійкість якої оцінюється, беруть стан спокою? Ні, не завжди. В загальному випадку можна говорити про стійкість руху взагалі, тобто руху, пов’язаного з будь-яким переміщенням маси або енергії. Наприклад, можна оцінити стійкість руху супутника, як його здатність повертатись на вихідну орбіту після припинення дії сил, які відхиляли супутник від заданої орбіти. Так само можна оцінити стійкість системи автоматичного управління, як її здатність повертатись до початкового незбуреного руху після припинення дій збурення.
Отже, ми розглянули якісну оцінку поняття стійкості. Але існує і кількісна оцінка цього поняття: стійкість можна описати математичними формулами.
Вперше найбільш суттєві математичні результати по стійкості механічних систем були отримані харків’янином А.М.Ляпуновим у 1880-1910 рр. Оскільки різні за своєю природою матеріальні системи описуються однаковими диференціальними рівняннями, то результати по стійкості механічних систем, отримані А.М.Ляпуновим, можна використати і до інших фізичних систем, в тому числі до систем автоматичного керування.
Стійкість є дуже важливою характеристикою якості систем і пристроїв, що використовуються в різних галузях техніки. Особливо гостро проблема стійкості стоїть в автоматиці. Це пояснюється наступним. Автоматичні системи є замкнутими системами, в яких вихідна величина через основний зворотний зв’язок подається на вхід системи, де порівнюється з заданим впливом. Система, що нормально функціонує, бажає зменшити різницю між значеннями задаючого впливу і керуючої величини. Але інколи виходить так, що ця різниця буде не зменшуватись, а зростати з плином часу, тобто система буде нестійкою. Характерно, що нестійкою може бути система, яка складається тільки зі стійких елементів, як це часто буває на практиці.
Через складність автоматичних систем для оцінки їх стійкості тільки фізичних уявлень недостатньо. Для цього необхідне використання математичного апарата. Тому розглянемо, в чому полягає особливість математичного трактування стійкості автоматичних систем.
|
|