Т а б л и ц а 5.1

Станки	Количество обработанных на станке деталей вида
		…
			…
…	…	…	…	…
			…
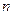
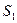
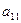
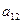
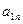
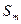
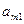
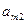
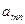
Число деталей в одном комплекте			…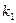

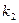
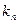
Составим математическую модель станковой задачи. Пусть 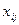– часть рабочего дня, в течение которой на 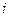-м станке обрабатываются детали 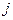-го вида, , 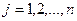. Тогда план работы станков можно представить матрицей

X=	Станки	Детали вида
		…	n
			…
…	…	…	…	…
			…

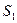
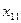
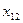
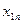
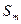
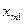
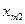
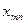
Обозначим через 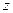число комплектов деталей, которое будет получено в соответствии с этим планом.

Принимая рабочий день за единицу, составим систему ограничений. Суммарное время работы каждого станка по обработке всех деталей не должно превышать рабочего дня, тогда

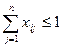, . (5.1)

Время, затраченное каждым станком по обработке деталей каждого вида, не может принимать отрицательное значение, поэтому должны выполняться неравенства

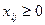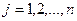, , . (5.2)

Количество деталей 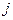-го вида, обработанных всеми станками по плану 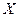равно 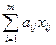. Поскольку в один полный комплект входит 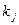деталей 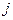-го вида, то из этих деталей можно было бы получить 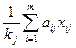комплектов. Подразумевается, что это количество округляется до целого в меньшую сторону. В один полный комплект входят детали разных видов, поэтому общее число комплектов равно

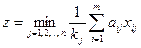. (5.3)

По условию это число должно быть максимальным. Тогда получим задачу максимизации целевой функции (5.3) при условии, что неизестные удовлетворяют системе ограничений (5.1)-(5.2).

Математическая модель (5.1)-(5.3) представляет собой задачу выпуклого программирования. Действительно, поскольку система ограничений состоит из линейных неравенств, то допустимая область задачи является выпуклой. Целевая функция (5.3) представляет собой минимум из линейных функций. Нетрудно доказать, что если функции 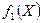, , 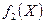…, 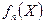– линейны, то функция 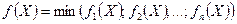является вогнутой. Это утверждение рекомендуется доказать самостоятельно, исходя из определения вогнутой функции нескольких переменных. В случае функций одной переменной указанное утверждение можно пояснить геометрически. На рис. 5.1 представлены графики трех линейных функций (прямые линии) и минимум этих функций (жирная ломаная линия). Очевидно, что эта последняя функция вогнута.

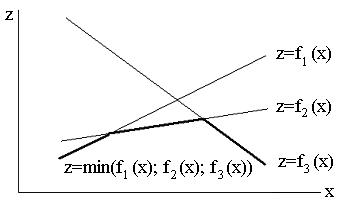
Рис. 5.1. Иллюстрация вогнутой функции

Тем самым задача (5.1)-(5.3) есть задача максимизации вогнутой функции 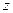на выпуклой допустимой области, и, следовательно, математическая модель относится к выпуклому программированию.