Сведения из теории. В общем виде задача оптимизации ставится следующим образом: требуется найти совокупность чисел , для которых функция

В общем виде задача оптимизации ставится следующим образом: требуется найти совокупность чисел 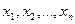, для которых функция

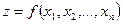(1.1)

достигает наибольшего (наименьшего) значения, и при этом выполняются условия

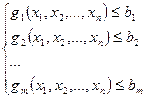. (1.2)

Функция (1.1) носит название целевой функции или функции цели, неравенства (1.2) образуют систему ограничений. В этой системе могут быть также неравенства вида 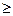, или равенства.

По смыслу задачи неизвестные 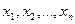, как правило, являются неотрицательными, то есть 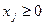, 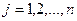. Эти условия могут содержаться среди неравенств (1.2), но могут также быть выписаны отдельно. Часть или даже все неизвестные задачи иногда должны быть целыми, тогда эти условия также включаются в систему ограничений.

Количество ограничений 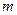и число неизвестных 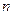характеризуют размерность задачи оптимизации.

Таким образом, в состав моделей оптимизации входят:

· целевая функция, выражающая в математической форме поставленную цель с точки зрения выбранного критерия оптимальности;

· система ограничений, то есть соотношения, которым должно удовлетворять решение данной задачи.

Любой набор переменных, удовлетворяющих системе ограничений, называется допустимым решением или планом. Совокупность всех допустимых решений называется допустимым множеством. Численные значения целевой функции позволяют определить качество различных допустимых решений в соответствии с выбранным критерием. Оптимальное решение (оптимальный план) представляет собой такое допустимое решение, при котором значение целевой функции достигает экстремальной величины.

Таким образом, если 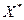– оптимальное решение задачи на максимум, то выполняется неравенство 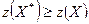для любого допустимого решения 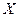. В случае задачи на минимум имеет место неравенство противоположного смысла.

В зависимости от вида целевой функции и ограничительных условий в задачах оптимизации принято выделять следующие разделы:

· линейное программирование, в котором целевая функция, а также уравнения и неравенства системы ограничений линейны;

· квадратичное программирование, в котором целевая функция квадратична и выпукла, а допустимое множество определяется линейными равенствами и неравенствами;

· выпуклое программирование, в котором целевая функция и допустимое множество выпуклы;

· дискретное программирование, в котором допустимое множество дискретно, например, состоит из точек с целочисленными координатами;

· сепарабельное программирование, в котором целевая функция и ограничения являются сепарабельными функциями, т.е. представляют собой сумму функций, каждая из которых зависит только от одной переменной;

· динамическое программирование, в котором процесс оптимизации разбивается на ряд последовательных этапов;

· стохастическое программирование, в котором информация о задаче оптимизации носит элементы неопределенности, и некоторые ее параметры являются случайными величинами.

Основным и важнейшим методом линейной оптимизации является в настоящее время симплексный метод или метод последовательного улучшения базисного плана. Метод был разработан Дж.Данцигом в 1949 году. Но еще раньше, в 1939 году, советским ученым академиком Л.В.Канторовичем для решения задач линейного программирования был предложен так называемый метод разрешающих множителей, незначительно отличающийся от симплексного метода. Симплекс-метод дает возможность решать задачи линейного программирования как вручную, так и на вычислительных машинах. Через конечное число шагов (симплексных таблиц) или получается оптимальное решение или обнаруживается неразрешимость задачи линейного программирования.

Для решения общей задачи нелинейной оптимизации существует довольно много алгоритмов, однако лишь немногие оказываются эффективными для задач большой размерности. Ни один из этих алгоритмов не имеет по отношению к другим таких преимуществ, чтобы его можно было считать универсальным средством решения любых задач нелинейного программирования. При сравнении алгоритмов следует использовать следующие критерии: надежность, скорость решения, время подготовки задачи для решения, точность решения, степень выполнения ограничивающих условий. Методы нелинейной оптимизации принято классифицировать в зависимости от порядка производных, которые используются для максимизации (минимизации) целевой функции:

· методы нулевого порядка (методы поиска), при которых для поиска точки экстремума используются только значения целевой функции;

· методы первого порядка, при которых используются значения целевой функции и ее первых частных производных;

· методы второго порядка, при которых используются значения целевой функции и ее первых и вторых частных производных;

К методам поиска относятся: метод покоординатного спуска Пауэлла, метод Хука-Дживса, метод Розенброка, метод деформируемого многогранника (симплексный метод Нелдера и Мида) и его модификация в виде комплексного метода Бокса для нелинейной оптимизации с ограничениями, методы случайного поиска.

К методам 1-го порядка относятся градиентные методы, метод сопряженных направлений, метод переменной метрики (Дэвидона-Флетчера-Пауэлла).

К методам 2-го порядка относится метод Ньютона.

Характерной особенностью вычислительной стороны методов решения задач оптимизации является то, что практическое использование этих методов требует огромной вычислительной работы, которую без ЭВМ реализовать крайне трудно, а в ряде случаев – невозможно. В первую очередь это связано с тем, что задачи оптимизации, формализующие реальные производственные ситуации, являются задачами большой размерности, недоступными для ручного счета.

Практическую реализацию методов оптимизации для учебных задач невысокой размерности удобно проводить средствами табличного процессора Microsoft Excel. Вычислительные возможности оптимизации объединены здесь с большим набором функций, присущих текстовому и графическому редакторам и другим приложениям пакета Microsoft Office. Excel позволяет выполнять линейную и нелинейную оптимизацию (для достаточно гладких функци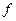й и 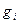, входящих в задачу), осуществлять прогнозирование и поддержку принятия решений.

Важное достоинство табличного процессора состоит в возможности автоматического пересчета всех данных, связанных функциональными зависимостями, при изменении любого компонента таблицы. Тем самым студент может в определенной степени управлять процессом оптимизации и принятия решений.