Определение криволинейного интеграла второго рода.

В этом разделе мы познакомимся с еще одним типом криволинейных интегралов.

Начнем с определения ориентированной кривой в пространстве.

Определение 1. Кривую Г, определяемую уравнением

,

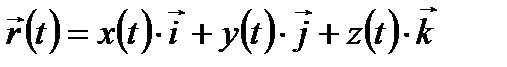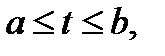
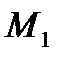будем называть ориентированной кривой, если на ней задан порядок следования точек, а именно, точка следует за точкой , если радиус-вектор 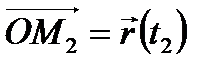точки отвечает значению параметра 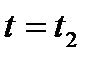большему, чем значение параметра 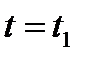радиус-вектора 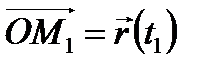точки 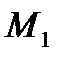, т.е. 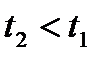. Точка А с радиус-вектором 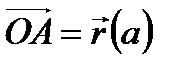называется началом кривой, а точка В с радиус-вектором 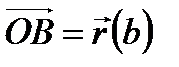– концом кривой (см. рис.1).

ПРИМЕР 1. Для окружности на плоскости OXY (см. рис. 10) радиус-векторы точек в параметрическом виде можно определить выражением:

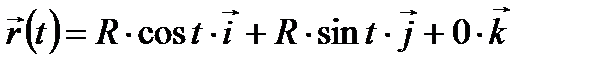, 0 ≤ t ≤ 2π.

Эта кривая – ориентированная: при возрастании параметра t от значения t = 0,

отвечающего точке A происходит движение соответствующей точки кривой против часовой стрелки до точки B (для которой t = 2π).

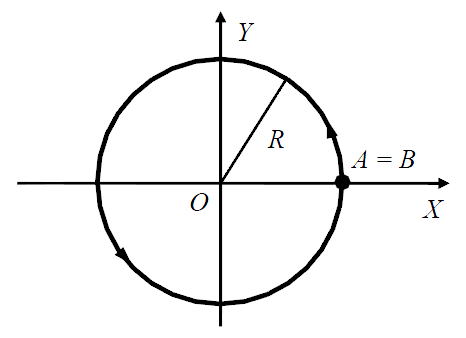
Рис.10. К примеру 1.

При построении разбиения Т в этом параграфе будем предполагать, что точки разбиения 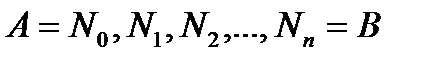следуют друг за другом. Обозначим через 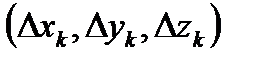координаты вектора 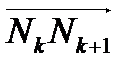. Пусть на кривой определены три непрерывные функции: P (x, y, z), Q (x, y, z) и R (x, y, z). Тогда можно считать, что на кривой Г задана вектор-функция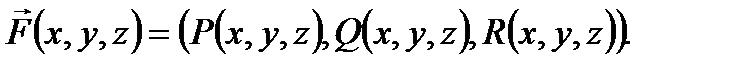

Составим три интегральные суммы:

a)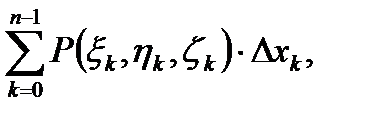

б)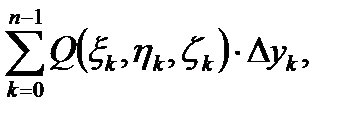

в)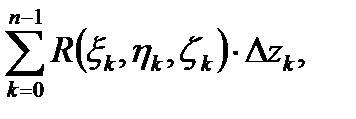

(1)

Теперь можно дать определение криволинейного интеграла второго рода.

Определение 2. Пусть существуют пределы интегральных сумм (1) при бесконечном увеличении числа точек деления и бесконечном уменьшении длин векторов , причем эти пределы не зависят ни от способа разбиения кривой Г, ни от выбора точек на дугах:

а)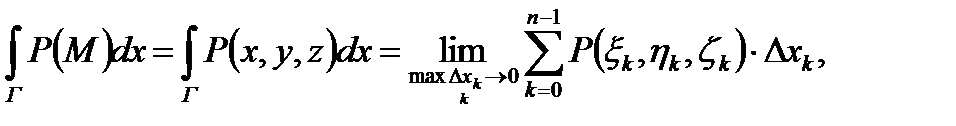

б)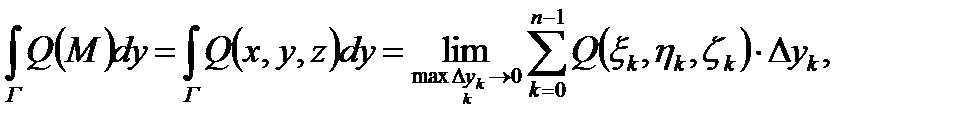

в)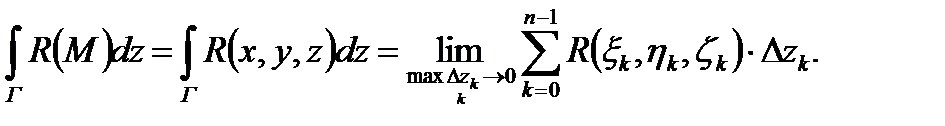

(2)

Тогда криволинейным интегралом второго рода, или криволинейный интеграл от векторной функции 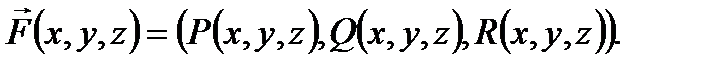вдоль ориентированной кривой Г, называется сумма интегралов, определенных формулой (2):

(3)

(В левой части равенства (3) под интегралом стоит скалярное произведение вектора 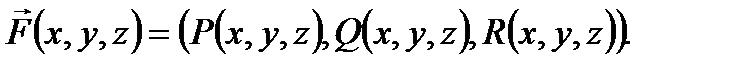на вектор )

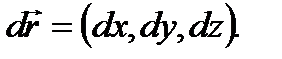Определение 3. Если кривая Г замкнута, то криволинейный интеграл, определяемый формулой (3), называется циркуляцией вектора 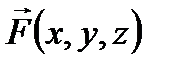по контуру Г. Для циркуляции обычно используется обозначение

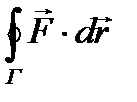
Как и в случае криволинейных интегралов первого рода, верна теорема:

Теорема 1. Если Г – кусочно-гладкая кривая и вектор 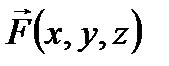имеет непрерывные на Г компоненты P (x, y, z), Q (x, y, z) и R (x, y, z), то криволинейные интегралы (2) и (3) существуют и определены однозначно. Используя формулу для дифференцирования сложной функции получаем еще одно утверждение:

Теорема 2. Если кривая Г задается векторным уравнением (1) п. 1.1, то интеграл (3) вычисляется по формуле:

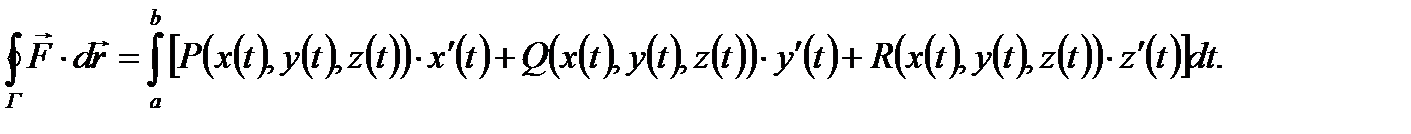
Аналогичные формулы справедливы для каждого из интегралов (2).

Замечание. Криволинейный интеграл второго рода, в отличие от криволинейного интеграла первого рода, зависит от ориентации кривой.

При изменении ориентации (заданного направления движения по кривой) интегралы (2) – (4) меняют знак. Это связано с тем, что в определении криволинейного интеграла второго рода в интегральных суммах (1) значения координат Δ xk, Δ yk, Δ zk меняют знак при изменении направления векторов 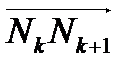на противоположное. В криволинейном интеграле первого рода изменения знака не происходит, поскольку в соответствующей интегральной сумме (2) из п. 1.1 величины Δ sk – длины дуг разбиения, которые не изменяются при изменении направления обхода кривой.

ПРИМЕР 2. Найти циркуляцию вектора 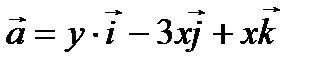вдоль контура 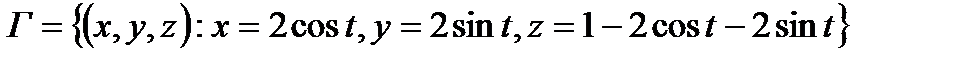в направлении возрастания параметра t (см. рис. 11).

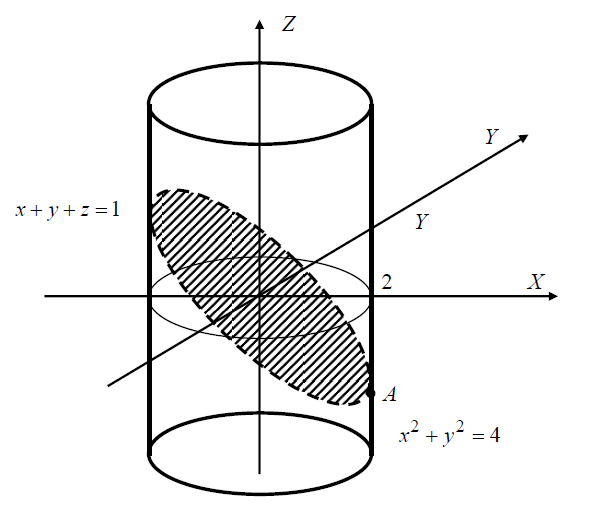
Рис.11. К примеру 2.

Заметим сначала, что для точек, лежащих на контуре Г справедливы соотношения: 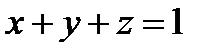и 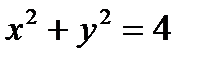, т.е. кривая Г есть замкнутая линия пересечения цилиндра 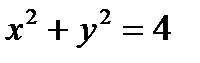с плоскостью .

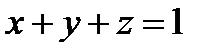Если начать движение по кривой Г от точки A (2, 0, – 1) в которой значение параметра t равно 0, то при изменении параметра t до значения 2π, точка кривой вернется в исходную точку A. Используя теорему 2, можно записать:

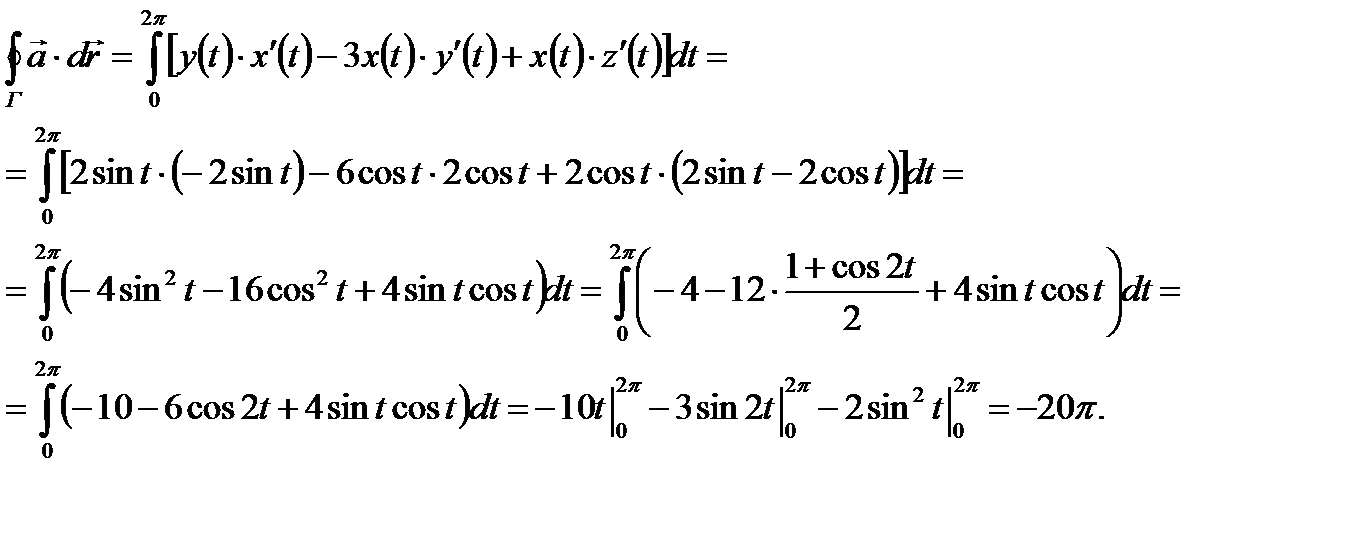
ПРИМЕР 3. Найти модуль циркуляции вектора 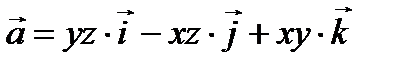вдоль контура

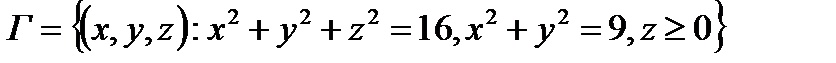(см. рис. 12).

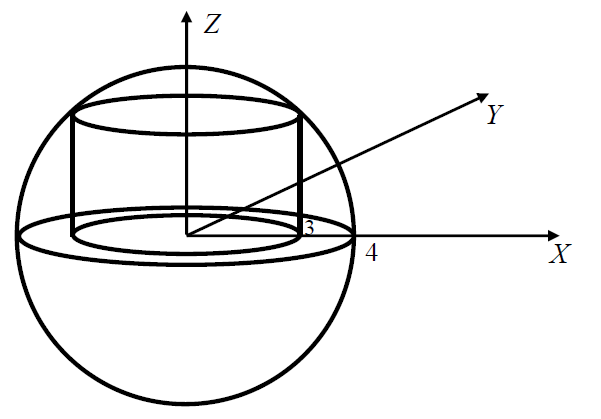
Рис.12. К примеру 3.

Для точек (x, y, z), лежащих на контуре Г, можно записать: 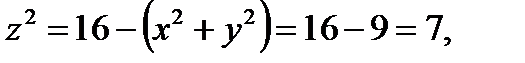откуда, учитывая условие 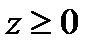, получаем 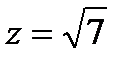. Поскольку для точек кривой Г выполнено соотношение 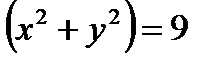, на ней можно ввести параметризацию: .

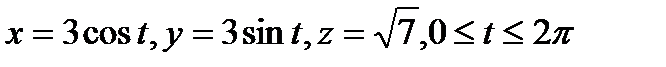Поскольку в примере требуется найти модуль циркуляции, то направление обхода кривой не имеет значения (при его изменении на противоположный меняется знак всего криволинейного интеграла второго рода, а значит и циркуляции). Примем, что движение по кривой происходит в сторону увеличения параметра t. Применяя теорему 2, получим:

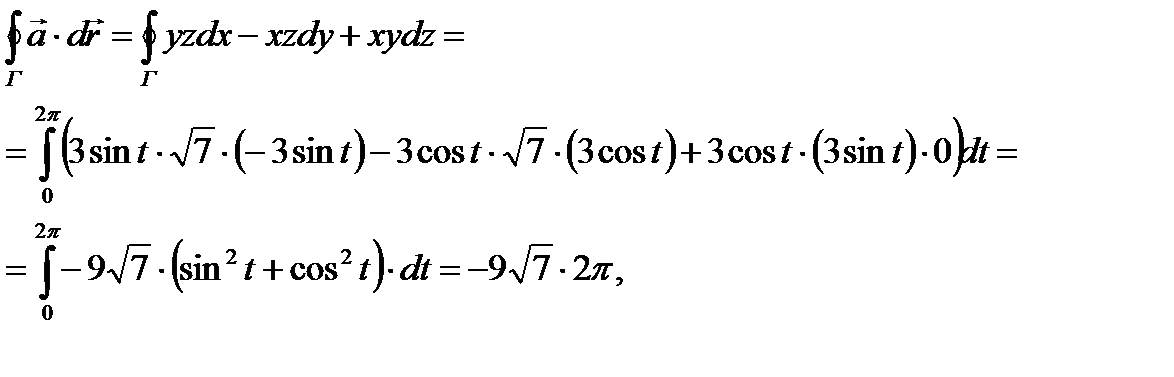
откуда модуль циркуляции равен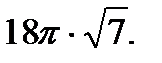

Замечание. Все определения и утверждения, сформулированные выше для пространственных кривых, справедливы и в случае плоских кривых. В соответствующих формулах нужно лишь убрать третью координату z (t).