
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дробный факторный эксперимент.
|
|
Дробный факторный эксперимент (ДФЭ) называют эксперимент, реализующий часть (дробную реплику) полного факторного эксперимента. ДФЭ позволяет определять параметры линейной модели при минимуме опытов.
При линейном росте числа независимых факторов 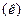 число экспериментов полного факторного плана (ПФП) растет как
число экспериментов полного факторного плана (ПФП) растет как 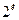 . Таким образом, количество опытов в ПФЭ значительно превосходит число определяемых коэффициентов линейной модели. Во многих практических задачах влияние взаимодействий второго и более высоких порядков пренебрежимо мало.
. Таким образом, количество опытов в ПФЭ значительно превосходит число определяемых коэффициентов линейной модели. Во многих практических задачах влияние взаимодействий второго и более высоких порядков пренебрежимо мало.
Эффективность ПФЭ при линейном моделировании невысока из-за разности между числом опытов и числом коэффициентов линейной модели. Другими словами, ПФЭ обладает избыточностью опытов. Возможно ли сократить число опытов за счет той информации, которая не очень существенна при построении линейных моделей?
Правило сокращения числа опытов формулируется следующим образом: чтобы сократить число опытов, нужно новому фактору присвоить вектор-столбец МП, принадлежащий взаимодействию, которым можно пренебречь. Тогда значение нового фактора в условиях опытов определяется знаками этого столбца.
Пример: для 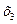 использован вектор-столбец
использован вектор-столбец 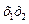 ПФЭ
ПФЭ 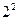 .
.
Наличие четырех опытов позволяет оценить четыре параметра линейной модели: 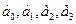 .
.
Таблица 4 Пример построения дробного факторного плана 23-1
| Номер опыта | 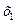
| 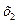
| 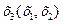
| 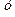
|
| - | - | + | 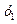
| |
| + | - | - | 
| |
| - | + | - | 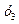
| |
| + | + | + | 
|
Возникает два вопроса?
1. Возможно ли получать при таком планировании несмешанные оценки параметров линейной модели?
2. Как выбирать a'priori взаимодействия, которые можно заменить на новый фактор?
Применение ДФЭ всегда связано с совместным оцениванием нескольких коэффициентов математической модели. Например, для выше приведенного примера, каждый из найденных коэффициентов  содержит оценку двух теоретических коэффициентов регрессии:
содержит оценку двух теоретических коэффициентов регрессии:
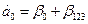 ;
;  ;
; 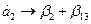 ;
; 
Указанные теоретические коэффициенты не могут быть оценены раздельно, так как вектор-столбцы МП для линейных членов и парных произведений совпадают (иначе говоря – полностью коррелированны).
Для обозначения дробных реплик, в которых 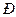 линейных эффектов приравнены к эффектам взаимодействия, используют условную запись
линейных эффектов приравнены к эффектам взаимодействия, используют условную запись 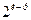 , где
, где 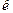 – общее число независимых факторов.
– общее число независимых факторов.
Условное обозначение дробных реплик.
Таблица 5 Примеры и условные обозначения дробных реплик.
| Число факторов | Дробная реплика | Условное обозначение | Число опытов | |
| ДФЭ | ПФЭ | |||
| 1/2 реплика от 23 | 23-1 | |||
| 1/2 реплика от 24 | 24-1 | |||
| 1/4 реплика от 25 | 25-2 | |||
| 1/8 реплика от 26 | 26-3 |
Для получения системы совместных оценок и анализа разрешающей способности дробных реплик используют понятия генерирующего и определяющего соотношения (определяющего контраста).
Определяющее соотношение (определяющей контраст) – это соотношение, задающее элементы столбца МП для фиктивной переменной (всегда равно +1 или -1). Получают перемножением элементов вектор-столбцов МП: 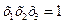 ;
; 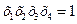 и т.д.
и т.д.
Определяющее соотношение помогает определять смешанные эффекты. Соотношения, задающие эти оценки можно найти, последовательно перемножая независимые факторы на определяющее соотношение. Например, для 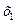 смешанный эффект определяется как
смешанный эффект определяется как  , где
, где 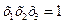 . Так как
. Так как 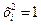 всегда, то
всегда, то 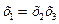 и т.д.
и т.д.
Генерирующее соотношение – соотношение служащее для построения дробной реплики. В рассмотренном примере, это: 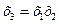 . Это соотношение показывающее, с каким из эффектов смешан данный эффект.
. Это соотношение показывающее, с каким из эффектов смешан данный эффект.
Разрешающая способность полуреплик определяется их генерирующим соотношением. Разрешающая способность тем выше, чем более высок порядок взаимодействий, с коэффициентами которых смешаны линейные коэффициенты.
Построение ДФП требует обязательного анализа смешивания основных эффектов с эффектами взаимодействия. Это позволяет точно представлять, какую информацию приходится терять в дробных планах.
Пример выбора полуреплик для ДФП 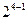 . Возможны следующие решения:
. Возможны следующие решения:
1)  5)
5) 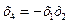
2) 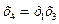 6)
6) 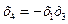
3) 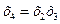 7)
7) 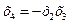
4) 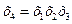 8)
8) 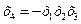
Наибольшая разрешающая способность у реплик 4 и 8. Их следует выбирать в первую очередь, т.к. тройные взаимодействия обычно менее важны чем парные в линейных моделях.
Определяющее соотношение  (т.е. возьмем полуреплику для которой контраст равен +1. В принципе можно взять другую полуреплику для которой контраст равен
(т.е. возьмем полуреплику для которой контраст равен +1. В принципе можно взять другую полуреплику для которой контраст равен 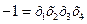 ). Тогда генерирующее соотношение
). Тогда генерирующее соотношение 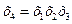 .
.
Получаем следующие совместные оценки:
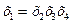
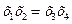
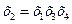
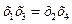
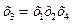
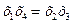
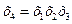
Следовательно параметры линейной модели:
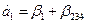
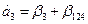
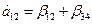
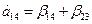
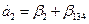
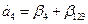
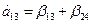
ПРИМЕРНЫЕ ВОПРОСЫ ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНУ ПО РАЗДЕЛУ 2
1. Понятие «алгоритм расчета». Примеры алгоритмов расчета. Вычислительный алгоритм.
2. Источники и классификация погрешностей численного решения задач.
3. Понятие абсолютной и относительной погрешности. Правила определения погрешности вычисления.
4. Форма записи числовых данных в памяти ЭВМ и погрешность машинных вычислений.
5. Постановка задачи о приближении функций. Понятия точечного и интегрального приближения. Экстраполяция. Вид обычного и тригонометрического интерполяционных полиномов.
6. Интерполирование функций (общие положения).
7. Интерполирование многочленами Лагранжа. Точность интерполирования многочленами Лагранжа.
8. Понятие конечных разностей и их свойства.
9. Интерполяционный полином Ньютона. Использование полинома Ньютона для построения формул линейного и квадратичного интерполирования. Точность интерполирования полиномами Ньютона.
10. Интерполирование периодических функций обобщенными тригонометрическими полиномами.
11. Понятие «гармонический анализ». Гармоники. Вычисление коэффициентов Фурье для четных и нечетных функций.
12. Общие сведения об интерполяции сплайнами. Определение коэффициентов кубического сплайна.
13. Точечное и интегральное квадратичное аппроксимирование функций.
14. Понятие ортогональных функций и системы ортогональных функций. Аппроксимирование ортогональными функциями.
15. Основные свойства обобщенного полинома степени m с коэффициентами Фурье. Понятие нормы элемента х, полной и неполной систем функций, условие полноты.
16. Равномерное приближение функций методом расчета среднего квадратичного отклонения.
17. Роль численных методов в решении алгебраических уравнений. Метод вложенных отрезков.
18. Понятие итерации и реккурентной формулы. Метод простой итерации (последовательных приближений). Достаточные условия сходимости итерационного процесса.
19. Общие сведения о решении алгебраических уравнений итерационными методами. Метод касательных.
20. Понятие итерации и реккурентной формулы. Метод секущих.
21. Метод простой итерации (последовательных приближений). Достаточные условия сходимости итерационного процесса. Метод хорд.
22. Понятие точных и приближенных методов решения систем линейных алгебраических уравнений. Метод Зейделя.
23. Понятие точных и приближенных методов решения систем линейных алгебраических уравнений. Сущность метода Гаусса и правила Крамера.
24. Понятие стационарных и нестационарных, явных и неявных итерационных методов решения систем линейных уравнений. Метод простой итерации.
25. Интерполирование многочленами Лагранжа. Построить многочлен L3(x) при следующих условиях: L3/(1) = 1, L3(0) = 1, L3(-1) = 1, L3(2) = 0.
26. Интерполирование многочленами Лагранжа. Построить многочлен L3(x) при следующих условиях: L3(-1) = 0, L3(1) = 1, L3(2) = 2, a1 = 1.
27. Понятие разделенных разностей и их свойства. Понятия «интегральная сумма», «квадратурная формула».
28. Численное дифференцирование в случае равностоящих узлов путем замены функции интерполяционным многочленом.
29. Численное дифференцирование в случае равностоящих узлов методом неопределенных коэффициентов.
30. Вычислительная погрешность формул численного дифференцирования. Выбор оптимального шага дифференцирования.
31. Квадратурная формула прямоугольников. Допущения при выводе данной формулы. Оценка погрешности численного интегрирования. Геометрическая интерпретация формулы прямоугольников.
32. Квадратурная формула трапеций. Допущения при выводе данной формулы. Оценка погрешности формулы трапеций, геометрическая интерпретация формулы трапеций.
33. Квадратурная формула Симпсона, допущенная при выводе формулы, оценка погрешности численного интегрирования.
34. Метод (правило) Ромберга.
35. Решение задачи Коши с помощью степенных рядов.
36. Метод Эйлера (ломаных) решения обыкновенных дифференциальных уравнений. Геометрическое построение ломаной Эйлера. Недостатки метода.
37. Модификации метода Эйлера численного решения задачи Коши (усовершенствованный метод ломаных и метод Эйлера-Коши).
38. Формулировка задачи Коши. Общая характеристика методов Рунге-Кутта. Общие правила выбора метода численного решения задачи Коши.
39. Метод Адамса (суть метода, вывод формулы Адамса).
40. Общая характеристика многошаговых методов решения задачи Коши. Сущность метода Милна.
41. Метод неопределенных коэффициентов решения обыкновенных дифференциальных уравнений.
42. Особенности интегрирования систем дифференциальных уравнений и дифференциальных уравнений второго порядка.
43. Понятие краевой задачи для обыкновенного дифференциального уравнения. Запись краевой задачи в конечно-разностной форме.
44. Сущность метода прогонки численного решения краевых задач (на примере правой прогонки). Условия устойчивости метода прогонки.
45. Сущность метода аппроксимирующих функций численного решения краевых задач. Метод коллокации. Метод наименьших квадратов. (общие положения)
46. Суть метода сеток решения дифференциальных уравнений в частных производных. Понятия: «сетка» в одномерной и двумерной областях, «сеточная функция», «разностная схема». Неравномерные сетки. Треугольная сетка.
47. Применение метода сеток к решению уравнений эллиптического типа. Метод линейной интерполяции для граничных узлов сеточной области.
48. Метод сеток решения уравнений параболического типа. Явная разностная схема и ее устойчивость.
49. Неявная разностная схема решения уравнений параболического типа. Метод прогонки решения уравнения теплопроводности.
50. Общие сведения о решении методом сеток уравнений гиперболического типа.
51. Содержание задачи оптимизации. Понятие «целевая функция», «допустимое множество», «точка экстремума», «точка локального экстремума», «точка глобального экстремума».
52. Теорема Вейершрасса. Численное решение одномерных задач безусловной оптимизации (метод равномерного распределения точек и его модификация).
53. Сущность многомерных задач оптимизации. Метод покоординатного спуска.
54. Сущность численного решения экстремальных задач. Метод градиентного спуска. Метод наискорейшего спуска.
55. Сущность численного решения экстремальных задач. Особенности решения задач оптимизации вблизи области экстремума. Проблема многоэкстремальности.
56. Сущность методов численного решения задач на нахождение условного экстремума.
57. Задачи линейного программирования и их эквивалентность. Понятия «целевая функция», «план», «допустимая задача».
58. Геометрическая интерпретация задач линейного программирования.
59. Симплекс-метод решения задач линейного программирования.
60. Основные виды линейных интегральных уравнений. Решение интегральных уравнений методом замены интеграла квадратурной суммой.
61. Основные виды линейных интегральных уравнений. Решение интегральных уравнении методом замены ядра на вырожденное.
62. Сущность методов Монте-Карло (на примере вычисления определенного интеграла). Методы вычисление последовательности случайных чисел.
63. Понятия «моделирование» и «модель». В чем состоит цель моделирования? Что определяет вид модели?
64. Что такое модель? Классификация моделей.
65. Требования к моделям. Отношения подобия реального объекта и модели.
66. Идеализация и абстракция при моделировании. Примеры.
67. Что такое «математическая модель» и «математическое моделирование»? Классификация математических моделей.
68. Достоинства математического моделирования и его основные этапы.
69. Выбор адекватного математического аппарата для описания математической модели (на примере моделей движения твердого тела, сплошной среды, сильно разряженных газов).
70. Модель типа «черный ящик». Области применения. Требования к параметрам модели. Математическая формулировка модели.
71. Модель состава системы. Математическое описание модели состава.
72. Модель структуры. Граф, виды графов. Математическое описание модели структуры. Примеры моделей структуры.
73. Прямые задачи моделирования, характерные черты, основные проблемы построения. Приведите примеры таких задач.
74. Обратные задачи моделирования, их характерный признак. Условная классификация обратных задач. Приведите примеры таких задач.
75. Понятие некорректно поставленных задач математического моделирования.
76. Понятие комплексного сквозного моделирования сложных технологических объектов. Приведите примеры.
77. Особенности построения математических моделей управляемых технических систем. Критерий оценки соответствия системы цели управления.
78. Моделирование стохастических процессов.
РЕКОМЕНДУЕМАЯ УЧЕБНАЯ ЛИТЕРАТУРА
1. Исследования и изобретательство в машиностроении/ М.Ф.Пашкевич, А.А.Жолобов, Ж.А.Мрочек и др.; под общ. ред. М.Ф.Пашкевича.- Могилев, Бел.-Рос. унив-т, 2005.- 294 с.
2. Кузьмичев Д.А., Радкевич И.А., Смирнов А.Д. Автоматизация экспериментальных исследований. – М.: Наука, 1983. – 392с.
2. Полтавский В.В. Основы измерений физических величин.- Минск: БГТУ, 2005.- 273 с.
3. Письменный Д.Т. Конспект лекций по теории вероятности, математической статистике и случайным процессам. – М.: Айрис-Пресс, 2008. – 320с..
4. Гмурман В.Е. Теория вероятностей и математическая статистика.- Москва: Юрайт, 2009.- 479 с.
5. Махаринский Е., Ящерицын П.И. Планирование эксперимента в машиностроении.- Минск
6. Поршнев С.В. Вычислительная математика. Курс лекций. – СПб.: БХВ-Петербург, 2004. – 320с.
7. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учебное пособие.- М: Наука, 1987.- 600 с.
8. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений.- М: Наука, 1978.- 589 с.
9. Аршанов
10. Тихонов А.Н., Костомаров Д.П. Вводные лекции по прикладной математике.- М: Наука, 1984.- 192 с.
11. Тихонов А.Н., Кальнер В.Д. Гласко В.Б. Математическое моделирование технологических процессов и метод обратных задач в машиностроении.- М: Машиностроение, 1990.- 264 с.
12. Нестеров
Тарасик В.П. Математическое моделирование технических систем.- Мн: БГПА, 1997. - 120с.
Дополнительная литература
Боровиков В.П., Боровиков И.П. Statistica – статистический анализ и обработка данных в среде Windows. – М.: Информационно-издательский дом «Филинъ», 1998. – 608с.
Дьяконов В.П. и др. Новые информационные технологии /Уч. пособие/ Под ред. В.П. Дьяконова – М.: СОЛОН-Пресс, 2005. – 640с.
Корн Г., Корн Т. Справочник по математике для научных и инженерных работников.- М: Наука, 1978.- 832с.
Румшиский Л.З. Математическая обработка результатов эксперимента.- М: Наука, 1971.- 192с.
Сафонов А.И., Поварехо А.С., Новицкий С.Н. Математическое моделирование технических систем. Лабораторный практикум.- Мн: БНТУ, 2004.- 50 с.
Кетков Ю.Л., Кетков А.Ю., Шульц М.М. МАТLАВ 6.х: программирование численных методов.- СПб: БХВ-Петербург, 2004.- 672 с.
Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа.- М: Наука, 1967. - 368с.
Боровиков В.П., Ивченко Г.И. Прогнозирование в системе Statistica в среде Windows. – М.: Финансы и статистика, 1999. – 384с.
Боровиков В.П. Программа Statistica для студентов и инженеров. – М.: Компьютерпресс, 2001.
9. Волков Е.А. Численные методы.- СПб: изд-во Лань, 2004.- 256 с.
Основная литература.
1. Исследования и изобретательство в машиностроении/М.Ф.Пашкевич, А.А.Жолобов, Ж.А.Мрочек и др.; под общ. ред. М.Ф.Пашкевича.- Могилев, Бел.-Рос. унив-т, 2005.- 294 с.
2. Полтавский В.В. Основы измерений физических величин.- Минск: БГТУ, 2005.- 273 с.
3. СимоненковЮ.П. Общая теория измерений.- Брянск: БГТУ, 2005.- 155 с.
4. Боровиков В.П., Боровиков И.П. Statistica – статистический анализ и обработка данных в среде Windows. – М.: Информационно-издательский дом «Филинъ», 1998. – 608с.
5. Гмурман В.Е. Теория вероятностей и математическая статистика.- Москва: Юрайт, 2009.- 479 с.
6. Дьяконов В.П. и др. Новые информационные технологии /Уч. пособие/ Под ред. В.П. Дьяконова – М.: СОЛОН-Пресс, 2005. – 640с.
7. Письменный Д.Т. Конспект лекций по теории вероятности, математической статистике и случайным процессам. – М.: Айрис-Пресс, 2008. – 320с.
8. Поршнев С.В. Вычислительная математика. Курс лекций. – СПб.: БХВ-Петербург, 2004. – 320с.
9. Кетков Ю.Л., Кетков А.Ю., Шульц М.М. МАТLАВ 6.х: программирование численных методов.- СПб: БХВ-Петербург, 2004.- 672 с.
10. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы: Учебное пособие.- М: Наука, 1987.- 600 с.
11. Лебедева Г.И., Микулик Н.А. Прикладная математика. Математические модели в транспортных системах.- Минск: Асар, 2009.- 512 с.
12. Тихонов А.Н., Кальнер В.Д. Гласко В.Б. Математическое моделирование технологических процессов и метод обратных задач в машиностроении.- М: Машиностроение, 1990.- 264 с.
13. Розанов Л.Н. Вакуумная техника.- Москва: Машиностроение, 2007.- 189 с.
14. Волков Е.А. Численные методы.- СПб: изд-во Лань, 2004.- 256 с.
15. Махаринский Е., Ящерицын П.И. Планирование эксперимента в машиностроении.- Минск
16. Маркова, Адлер Планирование эксперимента в
Дополнительная литература.
1. Клаасен К.Б. Основы измерений. Датчики и электронные приборы.- Долгопрудный: Интеллект, 2008.- 350 с.
2. Корн Г., Корн Т. Справочник по математике для научных и инженерных работников.- М: Наука, 1978.- 832с.
3. Румшиский Л.З. Математическая обработка результатов эксперимента.- М: Наука, 1971.- 192с.
4. Сафонов А.И., Поварехо А.С., Новицкий С.Н. Математическое моделирование технических систем. Лабораторный практикум.- Мн: БНТУ, 2004.- 50 с.
5. Самарский А.А., Николаев Е.С. Методы решения сеточных уравнений.- М: Наука, 1978.- 589 с.
6. Тарасик В.П. Математическое моделирование технических систем.- Мн: БГПА, 1997. - 120с.
7. Демидович Б.П., Марон И.А., Шувалова Э.З. Численные методы анализа.- М: Наука, 1967. - 368с.
8. Боровиков В.П., Ивченко Г.И. Прогнозирование в системе Statistica в среде Windows. – М.: Финансы и статистика, 1999. – 384с.
9. Боровиков В.П. Программа Statistica для студентов и инженеров. – М.: Компьютерпресс, 2001.
10. Тихонов А.Н., Костомаров Д.П. Вводные лекции по прикладной математике.- М: Наука, 1984.- 192 с.
11. Пипко А.И. Основы вакуумной техники. – М.: Энергоатомиздат, 1992.-240с.
12. Самарский А.А. Введение в численные методы.- СПб: Лань, 2005.- 288 с.
13. Новик Ф.С. Математические методы планирования экспериментов в металловедении.- Москва: Институт стали и сплавов, 1972.- 132 с.
|
|