
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Численное интегрирование. При исследовании математических моделей часто возникает необходимость вычисления различного рода интегралов от соответствующих функций
|
|
При исследовании математических моделей часто возникает необходимость вычисления различного рода интегралов от соответствующих функций. Вместе с тем, применение формулы Ньютона-Лейбница 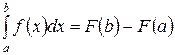 реализовать на практике не всегда возможно, поскольку первообразная не всех функций может быть выражена через элементарные или другие известные функции. В этих случаях применяют методы приближенного интегрирования, позволяющими найти численное значение определенного интеграла приближенно с любой точностью.
реализовать на практике не всегда возможно, поскольку первообразная не всех функций может быть выражена через элементарные или другие известные функции. В этих случаях применяют методы приближенного интегрирования, позволяющими найти численное значение определенного интеграла приближенно с любой точностью.
Идея численного (приближенного) интегрирования вытекает из геометрического смысла определенного интеграла – значение определенного интеграла численно равно площади криволинейной трапеции, ограниченной графиком функции 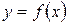 , осью абсцисс и прямыми
, осью абсцисс и прямыми 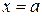 и
и 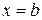 . Площадь криволинейной трапеции и является значением интеграла.
. Площадь криволинейной трапеции и является значением интеграла.
Формально процедура численного интегрирования заключается в том, что отрезок 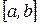 разбивается на
разбивается на 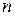 частичных отрезков, а затем подынтегральная функция заменяется на каждом отрезке легко интегрируемой функцией, интерполирующей значения подынтегральной функции в точках разбиения
частичных отрезков, а затем подынтегральная функция заменяется на каждом отрезке легко интегрируемой функцией, интерполирующей значения подынтегральной функции в точках разбиения
Наиболее простыми методами численного интегрирования являются:
1. Метод прямоугольников;
2. Метод трапеций;
А) Метод прямоугольников.
Разобьем сегмент 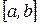 на
на 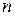 равных между собой частей с помощью точек:
равных между собой частей с помощью точек: 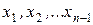 . Тогда длина части (в последующем – шаг интегрирования) определяется как
. Тогда длина части (в последующем – шаг интегрирования) определяется как  . В этом случае аргумент любой промежуточной точки разбиения
. В этом случае аргумент любой промежуточной точки разбиения 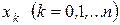 можно найти из соотношения
можно найти из соотношения 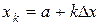 . Тогда можно представить ординату подынтегральной функции
. Тогда можно представить ординату подынтегральной функции 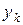 в виде
в виде 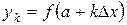 .
.
В этом случае суммы 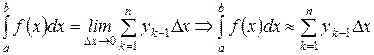 и
и 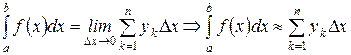 будут интегральными для функции
будут интегральными для функции 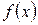 на отрезке
на отрезке 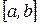 (при рассмотрении первой суммы в качестве значения функции на интервале
(при рассмотрении первой суммы в качестве значения функции на интервале 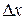 рассматриваются левые концы частичных сегментов (элементарный прямоугольник строится по левому концу сегмента), а при составлении второй – правые (см.рис.8, 9)).
рассматриваются левые концы частичных сегментов (элементарный прямоугольник строится по левому концу сегмента), а при составлении второй – правые (см.рис.8, 9)).
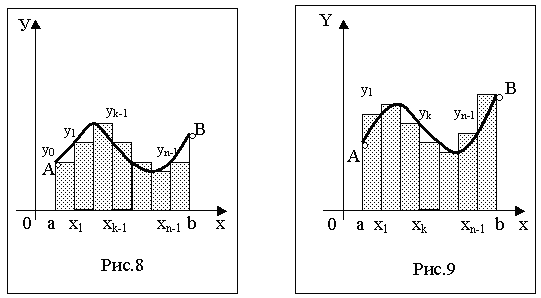
Окончательно формула прямоугольников имеет вид:
 - для рис 8. (20)
- для рис 8. (20)
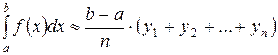 - для рис. 9. (21)
- для рис. 9. (21)
Метод прямоугольников – это наиболее простой и грубый метод приближенного интегрирования. Заметно меньшую погрешность дает другой метод – метод трапеций.
Б) Метод трапеций.
Чем больше число отрезков разбиения, тем более точный результат дает метод прямоугольников. Больший интерес представляют методы, дающие более точные результаты без увеличения числа точек разбиения. Простейшая из таких формул получается, как среднее арифметическое правых частей формул (20) и (21).
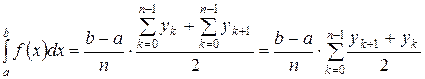 (22)
(22)
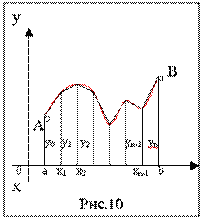
Геометрический смысл формулы заключается в замене подынтегральной функции на каждом отрезке разбиения стягивающей хордой (линейная интерполяция) и вычислении площади полученной трапеции (рис. 10), равной 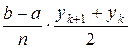
Приведя в формуле (22) подобные члены, окончательно получим формулу трапеций
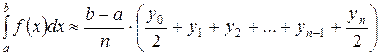
|
|