Композиция функций

Под композицией функций f и g будем понимать композицию отношений f и g и обозначать fog или gof. Ясно, что о композиции функций fog имеет смысл говорить, если 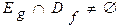. Однако, возникает вопрос: если даже отношение fog определено, то будет ли оно функцией? И какими свойствами обладает композиция двух функций? Ответ на первый вопрос дает теорема:

Теорема 1 (о композиции): Пусть g: A®B и f: B®C - функции. Тогда их композиция fog тоже является функцией, причем

1. D _fog={xÎ A| g(x)Î D_f}

2. (fog)(x)=f(g(x)) для каждого xÎ D _fog

3. fog={(x, f(g(x))|" x (g(x) Î D_f}

Доказательство:

По определению композиции отношений имеем: fog={(x, y)| $zÎ B ((x, z)Î gÙ (z, y)Î f)}. Так как g - функция, то для каждого x существует единственный zÎ B, а так как f - функция, ему не может соответствовать более одного y из C, поэтому если (x, y) Î fog и (x, y₁) Î fog, то y=y₁, так как z - один и тот же. Далее, из этого же равенства, если (x, y) Î g, то xÎ D_g и z=g(x) (1), а если (x, y) Î f и f - функция, то z=g(x)Î D_f (2) и y=f(z)=f(g(x)) (3). Чтобы композиция была определена (z существовал) необходимо и достаточно, чтобы g(x) Î D_f, но это и означает, что D_fog={xÎ A| g(x) Î D_f}, свойства 2) и 3) автоматически следуют из равенств (2) и (3).

Что и требовалось доказать.

Упражнение 1: Пусть f: A®B и g: B®C - функции. Что является областью определения функции gof, если:

a) f - функция, g - отображение

b) f - отображение, g - функция

c) f и g – отображения?

Вернемся к свойствам композиции.

Теорема 2: Пусть f: A®B и g: B®C - функции. Тогда:

a) если f и g инъективны, то gof инъективна

b) если f и g сюръективны, то gof сюръективна

c) если f и g биективны, то gof биективна.

Доказательство:

a) Пусть x₁, x₂Î D_gof и x₁¹ x₂. Пусть y₁=(gof)_(x1), а y₂= (gof)_(x2), но по теореме 1 y₁=g(f(x₁)) и y₂=g(f(x₂)). Но f(x₁)¹ f(x₂), в силу инъективности f, а значит g(f(x₁))¹ g(f(x₂)) в силу инъективности g.

b) самостоятельно

c) следует из а) и б)

Что и требовалось доказать.

Замечание: Если f и g вещественные функции, то gof или fog называют сложной функцией.

Пример 11: f: R ® R, x a sin x, g: R ® R, g: x a 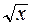, тогда fog: x asin , gof: x a . Найдите D_gof и D_fog.

Свойство 1(композиции): (fo g)o h= fo (go h).

Доказательство следует из соответствующего свойства отношений.