
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методика решения ЗЛП методом симплекс- таблиц
|
|
Практическая реализация ручного счета при использовании симплекс – метода в настоящее время используется в виде, так называемых, симплекс -таблиц, позволяющих в значительной мере формализовать процесс симплекс преобразований на каждом шаге. Такой метод решения ЗЛП получил название метод симплекс-таблиц. Вычислительной основой для реализации этого метода является метод полного исключения (метод Жордана – Гаусса).
Для определенности будем полагать, что задача решается но максимум целевой функции. Задача решается поэтапно.
Этап 1. После введения добавочных пере6менных систему уравнений ограничений и линейную форму (целевую функцию) запишем в виде расширенной постановки задачи
a11x1 + a12x2 + …+ a1nxn + xn+1 = b1,
a21x1 + a22x2 + …+ a2nxn + xn+2 = b2, (10.1)
……………………………………..
am1x1 + am2x2 + …+ amnxn + xn+m = bm.
F – c1x1 – c2x2 - … - cnxn = 0. (10.2)
При введении дополнительных переменных их коэффициентам придается такой же знак, что и знак у соответствующего свободного члена.
Этап 2. Исходную расширенную систему заносим в первую симплекс таблицу (таблица 10.1)
Таблица 10.1 – Исходная симплекс – таблица
| i | Базис | сб | P0 | c1 | c2 | ... | cr | ... | cm | cm+1 | ... | ck | ... | cn |
| P1 | p2 | ... | Pr | ... | Pm | Pm+1 | ... | Pk | ... | Pn | ||||
| P1 | c1 | b1 | ... | ... | a1m+1 | ... | a1k | ... | a1n | |||||
| P2 | c2 | b2 | ... | ... | a2m+1 | ... | a2k | ... | a2n | |||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| r | Pr | cr | br | ... | ... | arm+1 | ... | ark | ... | arn | ||||
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| m | Pm | cm | bm | ... | ... | amm+1 | ... | amk | ... | amn | ||||
| m+1 | F0 | ... | ... |  m+1 m+1
| ... |  k k
| ... |  n n
|
Таблица имеет m + 1 строку, где m – число базисных (основных) переменных. В последнюю (m + 1) записывается линейная форма. Эта строка таблицы называется оценочной.
Таблица имеет n + 4 столбца, где n – общее число переменных в расширенной задаче (заполняются, начиная с мятого столбца).
Столбец 1 – номер строки (1, 2, …, m, m+1).
Столбец 2 – Обозначение базисного вектора Р1, Р2, …, Pr, …, Pm.
В столбце 3 (Сб ) таблицы записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.
В столбце 4 (Ро) записывают положительные компоненты исходного опорного плана (свободные члены соответствующих уравнений). В нем же в результате вычислений получают положительные компоненты оптимального плана. Столбцы 5 - n +4 – столбцы векторов Pj. Вних заполняюткоэффициенты aij расширенной системы уравнений ограничений (разложения этих векторов по векторам данного базиса.
В таблице 3.1 первые m строк определяются исходными данными задачи, а показатели (m + 1)-й строки вычисляют. В этой строке в столбце вектора Ро записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора Рj — значение  j = zj — сj.
j = zj — сj.
Значение zj - вычисляется как скалярное произведение вектора Pj (j=l, n) на вектор Cб =(c1; c2;...; сm):
zj = 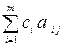 (j= 1, n) (10.3)
(j= 1, n) (10.3)
Значение F0 равно скалярному произведению вектора Pо на вектор Сб:
F0 = 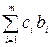 .(10.4)
.(10.4)
Далее таблица преобразуется по строго определенным формальным правилам.
Этап 3. После заполнения таблицы 10.1 исходный опорный план проверяют на оптимальность. Для этого просматривают элементы (m+1)-й строки таблицы. В результате может иметь место один из следующих трех случаев:
1)  j ³ 0 для j = m+1, m+2,..., n(при j=
j ³ 0 для j = m+1, m+2,..., n(при j= 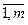 ; zj = cj). Поэтому в данном случае числа
; zj = cj). Поэтому в данном случае числа  j ³ 0 для всех j от 1 до n;
j ³ 0 для всех j от 1 до n;
2)  j < 0 для некоторого j, и все соответствующие этому индексу величины aij £ 0(i=l, m);
j < 0 для некоторого j, и все соответствующие этому индексу величины aij £ 0(i=l, m);
3)  j < О для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел aij положительно.
j < О для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел aij положительно.
В первом случае на основании признака оптимальности исходный опорный план является оптимальным. Задача решена.
Во втором случае целевая функция не ограничена сверху на множестве планов (задача не имеет решения).
В третьем случае получено решение является базисным допустимым, но не оптимальным. Имеется возможность улучшения плана. Можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится.
Этап 4. Переход от одного опорного плана к другому осуществляется исключением из исходного базиса одного из векторов и введением в него нового вектора.
В качестве вектора, вводимого в базис, можно взять любой из векторов Рj, имеющий индекс j, для которого  j < 0. Если таких столбцов несколько, то целесообразно взять тот столбец, у которого
j < 0. Если таких столбцов несколько, то целесообразно взять тот столбец, у которого  j по абсолютной величине наибольшее. Пусть, например,
j по абсолютной величине наибольшее. Пусть, например,  k < 0 и решено ввести в базис вектор Pk. Если же таких чисел несколько, то в базис вводят вектор, имеющий такой же индекс, как и максимальное из чисел Сj, определяемых данными числами
k < 0 и решено ввести в базис вектор Pk. Если же таких чисел несколько, то в базис вводят вектор, имеющий такой же индекс, как и максимальное из чисел Сj, определяемых данными числами  j (
j ( j < 0).
j < 0).
В данном случае, столбец, в котором записаны элементы вектора Pk называют направляющим.
Для определения вектора, выводимого (исключаемого) из базиса, определяют минимум отношения min (bi/aik) для всех аik > 0 (направляющего столбца). Пусть этот минимумдостигается при i = r. Тогда эту (i) строку называют направляющей, ииз базиса исключают вектор Рг, а число ark, находящееся на пересечении направляющего столбца и направляющей строки) называют разрешающим элементом.
При получении значения этого отношения могут возникнуть следующие ситуации:
- bi и air имеют разные знаки. Отношение принимается равным ∞ $;
- bi = 0 и air < 0. Отношение принимается равным ∞;
- air = 0. Отношение принимается равным ∞;
- bi = 0 и air > 0. Отношение принимается равным 0;
- если biC и aikC имеют одинаковые знаки. Отношение принимается равным 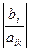 .
.
Этап 5. После выделения направляющей строки и направляющего столбца вычисляют новый опорный план и коэффициенты разложения векторов Pj через векторы нового базиса, соответствующего новому опорному плану. Составляется новая (в данном случае вторая) симплекс – таблица.
Получение новых элементов таблицы осуществляется на основе метода исключений (метода Жордана—Гаусса). При этом элементы новой таблицы вычисляются по формулам:
а) элементы столбца Р0:
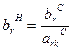 (10.5)
(10.5)
для строки, соответствующей направляющей в старой (в данном случае первой) таблице;
 (10.6)
(10.6)
где r –индекс (нижний) направляющей строки;
k - индекс (нижний направляющего столбца;
Н – индекс (верхний) элемента новой таблицы;
С - индекс (верхний) элемента старой таблицы.
Из этих обозначений следует, что ark – разрешающий элемент;
б) коэффициенты разложения векторов Pj через векторы нового базиса, соответствующего новому опорному плану— по формулам:
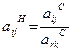 (10.7)
(10.7)
для строки, соответствующей направляющей в старой (в данном случае первой) таблице;
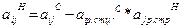 (10.8)
(10.8)
После вычисления biНи aijН согласно формулам (10.5)- (10.8) их значения заносят в новую таблицу.
Элементы (m+1)-й строки новой таблицы могут быть вычислены по формулам
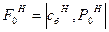 - (10.10)
- (10.10)
скалярное произведение векторов сб и Р0 новой таблицы;
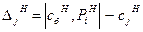 - (10.11)
- (10.11)
скалярное произведение векторов сб и Рi новой таблицы минус сj.
Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел Сj, определяемых данными числами  j (
j ( j < 0).
j < 0).
Итак, переход от одного опорного плана к другому сводится к переходу от одной симплекс-таблицы к другой. Элементы новой симплекс-таблицы можно вычислить как с помощью рекуррентных формул (10.5) — (10.11), так и по правилам, непосредственно вытекающим из них. Эти правила состоят в следующем.
В столбцах векторов, входящих в базис, на пересечении строк и столбцов одноименных векторов проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю.
Элементы векторов P0 и Pj в строке новой симплекс-таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце сб в строке вводимого вектора проставляют величину сk, где k — индекс вводимого вектора.
Остальные элементы столбцов вектора Ро и Pj новой симплекс-таблицы вычисляют по правилу треугольника. Для вычисления какого-нибудь из этих элементов получают три числа:
1) число, стоящее в исходной симплекс-таблице на месте искомого элемента новой симплекс-таблицы;
2) число, стоящее в исходной симплекс-таблице на пересечении строки, в которой находится искомый элемент новой симплекс-таблицы, и столбца, соответствующего вектору, вводимому в базис;
3) число, стоящее в новой симплекс-таблице на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимого в базис вектора (эта строка получается из строки исходной симплекс-таблицы делением ее элементов на разрешающий элемент).
Эти три числа образуют своеобразный треугольник, две вершины которого соответствуют числам, находящимся в исходной симплекс-таблице, а третья — числу, находящемуся в новой симплекс-таблице. Для определения искомого элемента новой симплекс-таблицы из первого числа вычитают произведение второго и третьего.
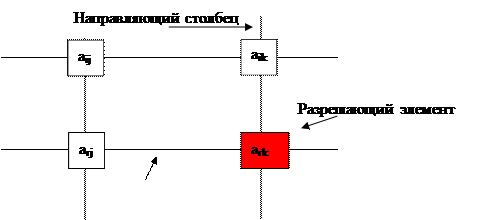
Отметим, что в некоторых источниках это правило трактуется, как правило прямоугольника и графически изображается так как показано на рисунке 10.1.
 |
|
Рисунок 10.1 – Графическое изображение правила прямоугольника
После заполнения новой симплекс-таблицы вновь просматривают элементы (m+1)-й строки. Если все ∆ jj ³ 0, то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную последовательность действий, вычисляют новый опорный план. Этот процесс продолжают до тех пор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость.
При получении решения задачи линейного программирования мы предполагали, что эта задача имеет опорные планы и каждый такой план является невырожденным. Если же задача имеет вырожденные опорные планы, то на одной из итераций одна или несколько переменных опорного плана могут оказаться равными нулю. Таким образом, при переходе от одного опорного плана к другому значение функции может остаться прежним. Более того, возможен случай, когда функция сохраняет свое значение в течение нескольких итераций, а также возможен возврат к первоначальному базису. В последнем случае обычно говорят, что произошло зацикливание. Однако при решении практических задач этот случай встречается очень редко, поэтому мы на нем останавливаться не будем.
Итак, вычисление оптимального плана симплексным методом включает следующие этапы:
1) вычисляют опорный план;
2) составляют симплекс-таблицу;
3) выясняют, имеется ли хотя бы одно отрицательное число  j. Если нет, то полученный опорный план оптимален. Если же среди чисел
j. Если нет, то полученный опорный план оптимален. Если же среди чисел  j имеются отрицательные, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану;
j имеются отрицательные, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану;
4) вычисляют направляющие столбец и строку. Направляющий столбец определяется наибольшим по абсолютной величине отрицательным числом  j, а направляющая строка — минимальным из отношений компонент столбца вектора P0 к положительным компонентам направляющего столбца;
j, а направляющая строка — минимальным из отношений компонент столбца вектора P0 к положительным компонентам направляющего столбца;
5) по формулам (10.5) — (10.11) определяют положительные компоненты нового опорного плана, коэффициенты разложения векторов Pj по векторам нового базиса и числа F0Н,  jН. Все эти числа записываются в новую симплекс-таблицу;
jН. Все эти числа записываются в новую симплекс-таблицу;
6) проверяют полученный опорный план на оптимальность. Если план не оптимален и необходимо перейти к новому опорному плану, то возвращаются к этапу 4. В случае получения оптимального плана или установления неразрешимости задачи процесс решения заканчивают.
|
|