
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод Гомори
|
|
Нахождение решения задачи целочисленного программирования методом Гомори начинают с определения симплексным методом оптимального плана задачи (1) — (3) без учета целочисленности переменных. После того как этот план найден, просматривают его компоненты. Если среди компонент нет дробных чисел, то найденный план является оптимальным планом задачи целочисленного программирования (1) — (4). Если же в оптимальном плане задачи (4) — (3) переменная X] принимает дробное значение, то к системе уравнений (3) добавляют неравенство
∑ f (a*ij) xj ≥ f (b*i ) (5)
j
и находят решение задачи (1) —(3), (5).
В неравенстве (5) a*ijи b*i — преобразованные исходные величины aijи bi, значения которых взяты из последней симплекс-таблицы, a f (a*ij) и f (b*i) — дробные части чисел (под дробной частью некоторого числа а понимается наименьшее неотрицательное число b такое, что разность между а и b есть целое). Если в оптимальном плане задачи (1) — (3) дробные значения
принимают несколько переменных, то дополнительное неравенство (5) определяется наибольшей дробной частью.
Если в найденном плане задачи (1) —(3), (5) переменные принимают дробные значения, то снова добавляют одно дополнительное ограничение и процесс вычислений повторяют. Проводя конечное число итераций, либо получают оптимальный план задачи целочисленного программирования (1) — (4), либо устанавливают ее неразрешимость.
Если требование целочисленности (4) относится лишь к некоторым переменным, то такие задачи называются частично целочисленными. Их решение также находят последовательным решением задач, каждая из которых получается из предыдущей с помощью введения дополнительного ограничения. В этом случае такое ограничение имеет вид
∑ yijxj ≥ f (b*i),
j
где yij определяются из следующих соотношений:
1) для xj которые могут принимать нецелочисленные значения,
|
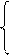 a*ij при a*ij≥ 0
a*ij при a*ij≥ 0

 f (b*i) a*ij при a*ij< 0;
f (b*i) a*ij при a*ij< 0;
 1- f (b*i)
1- f (b*i)
2) для Xj, которые могут принимать только целочисленные значения,

 f
f
|
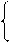 ( a*ij ) при f
( a*ij ) при f
|
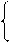 ( a*ij)≤ f (b*i)
( a*ij)≤ f (b*i)
f (b*i) 1-f ( a*ij) при f ( a*ij)> f (b*i)
 1- f (b*i)
1- f (b*i)
Из изложенного выше следует, что процесс определения оптимального плана задачи целочисленного программирования методом Гомори включает следующие основные этапы:
1. Используя симплексный метод, находят решение задачи (1)-(3) без учета требования целочисленности переменных.
2. Составляют дополнительное ограничение для переменной, которая в оптимальном плане задачи (1)—(3) имеет максимальное дробное значение, а в оптимальном плане задачи (1)—(4) должна быть целочисленной.
3. Используя двойственный симплекс-метод, находят решение задачи, получающейся из задачи (1)—(3) в результате присоединения дополнительного ограничения.
4. В случае необходимости составляют еще одно дополнительное ограничение и продолжают итерационный процесс до получения оптимального плана задачи (1)—(4) или установления ее неразрешимости.
Контрольные вопросы
- Какие задачи относятся к задачам целочисленного программирования?
- В чем сущность метода Гомори?
- Каким образом строится сечение Гомори?
- Сколько сечений Гомори можно построить?
- Чему равна дробная часть положительного числа?
- Чему равна дробная часть отрицательного числа?
- Определить дробную часть следующих чисел:
4/5; 8/3; -12/7; 65/57; -4/7; - 8/3
- Перечислить этапы алгоритма метода Гомори.
9. Тест на тему «Метод Гомори»
1.Задача целочисленного программирования - это……
а) разновидность транспортных задач.
б) экстремальная задача, переменные которой принимают лишь целочисленные значения.
в) вспомогательная задача, получаемая с помощью определенных правил непосредственно из условия исходной.
2. В математической модели задачи целочисленного программирования целевая функция и функция в системе ограничений могут быть:
а) линейными, нелинейными, смешенными.
б) только линейными.
в) нелинейными и смешенными.
3. Решение задачи целочисленного программирования начинают с …
а) определения симплексным методом оптимального плана задачи без учета целочисленности переменных.
б) построение двойственной к ней задачи.
в) приведение исходной системы к единому базису.
4. План считается оптимальным, если…
а) несколько переменных имеют дробное значение.
б) нет переменных с дробным значением.
в) все переменные имеют дробное значение.
5. В каком случае строится сечение Гомори?
а) если в оптимальном плане задачи нет дробных значений переменных.
б) все переменные имеют дробное значение.
в) если одна или несколько переменных принимают дробное значение.
|
|