
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Математическая постановка задачи
|
|
Классическая постановка транспортной задачи. Пусть имеется т поставщиков А1, А2,..., Аi,.., Ат однородного груза в количествах соответственно a1, a2, …, ai, …, amединиц и п потребителей В1, В2,..., Bj,..., Вп этого груза, потребность которых составляет соответственно b1, b2, …, bj, …, bnединиц.
Известны стоимости перевозок единицы груза от (i-го поставщика к j-му потребителю — С ij (i= 1, т; j=1, п).
Требуется составить такой план перевозок груза, который обеспечит минимальные транспортные расходы.
Замечание. Перевозимый груз должен быть однородным, например песок, уголь, лес, кирпичи, металл и т.п. Единицы измерения количества груза могут быть различными (т, м3, шт., л. и т.п.). Стоимость перевозки, как правило, измеряется в рублях. Предполагается, что стоимость перевозимого груза пропорциональна его количеству. В качестве поставщиков груза могут выступать предприятия, магазины, строительные объекты и т.п.
Прежде чем приступить к построению модели задачи, необходимо обозначить неизвестные. Исходя из условия задачи, неизвестной величиной является количество единиц груза, перевозимого от каждого поставщика к каждому потребителю. Обозначим через xij (i=1, m; j=1, n)- количество единиц груза, перевозимого от i-го поставщика к j-му потребителю.
Чтобы лучше представить условие задачи, сведём исходные данные в табл. 1. Строка таблицы соответствует поставщику, а столбец - потребителю.
Очевидно, общее наличие груза у поставщиков равно ∑ ai, а общая потребность в грузе в пунктах назначения равна ∑ bj единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.
∑ ai = ∑ bj (1)
то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
| x11 | c11 | x12 | c12 | … | c1j | … | x1n | c1n | |
| x1j | |||||||||
| x21 | c21 | c22 | … | c1j | … | x2n | c2n | ||
| x22 | x2j | ||||||||
| … | … | … | … | … | … | ||||
| xi1 | Ci1 | ci2 | … | xij | c1j | … | xin | cin | |
| xi2 | |||||||||
| … | … | … | … | … | … | ||||
| xm1 | cm1 | cm2 | … | cmj | … | xmn | cmn | ||
| xm2 | xmj |
Таблица
|
|
|
|
|
|
|
| |||||||||||||
 | ||||||||||||||||||
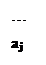 | ||||||||||||||||||
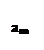 |
Теорема 2.1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. Чтобы выполнялось равенство (1).
Очевидно, общее наличие груза у поставщиков равно ∑ ai, а общая потребность в грузе в пунктах назначения равна ∑ bj единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е. то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
Теорема 2.1. Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. Чтобы выполнялось равенство (1).
Методы построения исходного плана
Для получения исходного плана используются различные методы, два из которых будут рассмотрены ниже.
Метод северо-западного угла.
Определение значений Хijначинается с левой верхней клетки таблицы (это соответствует северо-западному углу на географической карте). Находим значение Х11из соотношения
Х11=min {a1, b1}
Возможны три варианта:
1) если a1< b1, то Х11 = a1строка i=1исключается из дальнейшего рассмотрения, а потребность первого потребителя b1 (столбец j=1) уменьшается на величину a1.;
2) если a1> b1 \, то Х11 = b1, столбец j=1 исключается из дальнейшего рассмотрения, а наличие груза у первого поставщика
а 1(строка i=1 ) уменьшается на величину b1.
3) если a1 = b1, то Х11 = a1 = b1, строка i= 1и столбец j=1 исключаются из дальнейшего рассмотрения. Данный вариант приводит к вырождению исходного плана.
Затем аналогичные операции проделывают с оставшейся частью таблицы, начиная с ее северо-западного угла. На последнем шаге процесса останется одна строка и один столбец. После заполнения клетки, стоящей на их пересечении, процесс завершается.
После завершения описанного процесса необходимо провести проверку полученного плана на вырожденность. Если количество заполненных клеток равно m+n — 1, то план является невырожденным, в противном случае — вырожденным.
Если план вырожденный, т. е. количество заполненных клеток оказалось меньше m+n—1, то незаполненные клетки с минимальными стоимостями перевозок заполняются нулями, чтобы общее количество заполненных клеток стало равным m+n—1. Однако при расстановке нулей необходимо помнить, что в таблице не должно быть ни одного прямоугольника, все вершины которого являются заполненными клетками. Например, переменные x21, x22 или x11, x1n, x21, x2n(табл. 1) не могут быть одновременно базисными.
Например, зная запасы и потребности в сырье, распределить его по методу северо-западного угла.
| Bj Ai | |||||
Метод минимального элемента.
В отличие от метода северо-западного угла данный метод учитывает при построении исходного плана стоимости перевозок. В ряде случаев он позволяет получить лучший с точки зрения критерия оптимальности план, сокращая количество итераций для получения оптимального плана.
Определение значений Хijначинается с клетки, имеющей минимальную стоимость перевозки (если таких клеток более одной, то договоримся выбирать первую по порядку).
Как и в методе северо-западного угла, переменной, отвечающей выбранной клетке, присваивается минимальное из двух возможных значений. Соответствующая строка или столбец исключаются из дальнейшего рассмотрения, а потребность потребителя
или наличие груза у поставщика уменьшается на выбранную величину. Если для выбранной клетки с минимальной стоимостью перевозки наличие груза у поставщика равно потребности потребителя, то из дальнейшего рассмотрения исключаются строка и столбец.
Затем в оставшейся части таблицы проделывают аналогичные операции, опять начиная с клетки, имеющей минимальную стоимость перевозки. На последнем шаге процесса останется одна строка и один столбец. После заполнения клетки, стоящей на их пересечении, процесс завершается.
Проверка полученного плана на вырожденность и расстановка (в случае вырожденности плана) нулей осуществляется так же, как это описано для метода северо-западного угла.
Например, зная запасы и потребности в сырье, а также стоимости перевозок, распределить его по методу минимального элемента.
| bi ai | |||||||
| 5 | 8 | 3 | 10 | 4 | |||
| 10 | 7 40 | 9 | 6 | 5 | |||
| 7 | 3 | 6 | 4 50 | 12 | |||
| 6 | 3 | 11 | 5 | 4 |
|
|