
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод искусственного базиса (М-задача)
|
|
До сих пор при изложении симплексного метода предполагалось, что система исследуемых уравнений решена относительно базисных переменных, т. е приведена к единичному базису, и все Bi≥ 0.
Мы уже видели, что с помощью симплексных преобразований этого можно всегда добиться. Однако расчеты, с которыми сопряжены эти преобразования, порой оказываются даже более громоздкими, нежели последующие вычисления в симплексных таблицах. Поэтому рассмотрим другой метод, который связан с решением той же задачи определения исходного опорного решения и получивший название метода искусственного базиса
Он особенно удобен, когда число переменных значительно превосходит число уравнений.
Заметим, что в некоторых случаях получение исходного опорного решения не вызывает осложнений и не требует применения специальных приемов. Так, например, система исходных ограничений может оказаться сразу заданной в приведенном к единому базису виде с неотрицательными свободными членами. Иногда исходные ограничения могут выражаться неравенствами вида ai1 x1+ai2x2+…+ain xn≤ ai0 где аi0≥ 0.
Тогда, вводя балансовые переменные, получим эквивалентную систему уравнений, разрешенную относительно этих балансовых переменных.
Пусть задана каноническая форма задачи линейного программирования.
Максимизировать линейную функцию
Z=c1 x1+с2 х2+…+сk хk +…cn xn
в области решений системы уравнений
 a11x11+a12x12+…+a1nxn=b1
a11x11+a12x12+…+a1nxn=b1
a21x21+a22x22+…+a2nxn=b2
…………………………………………..
ai1xi1+ai2xi2+…+ainxn=bi
…………………………………………..
am1xm1+am2xm2+…+amnxn=bm
x1 ≥ 0; x2 ≥ 0; …; xn ≥ 0
Среди уравнений системы могут оказаться некоторые линейно зависимые от остальных, т. е. ранг систем может быть меньше, чем m, однако в излагаемом методе нет необходимости в предварительном определении ранга системы и отбрасывании “лишних” уравнений. Будем полагать, что все aio ≥ 0. Очевидно, этого всегда можно добиться умножением соответствующего уравнения на множитель —1.
 a11x1+a12x2+…+a1nxn+xn+1= b1
a11x1+a12x2+…+a1nxn+xn+1= b1
a21x1+a22x2+…+a2nxn+xn+2= b2
………………………………
ai1x1+ai2x2+…+ainxn+xn+i= bi
……………………………………………….
am1x1+am2x2+…+amnxn+xn+m= bm
получаемую из исходной системы введением m неотрицательных переменных хn+1 ≥ 0; хn+2 ≥ 0; …; хn+m ≥ 0, именуемых искусственными.
Исходная система уравнений приведена к единичному базису { 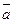 n+1 , …,
n+1 , …, 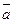 n+m }, называемому искусственным базисом, и имеет неотрицательный столбец свободных членов (
n+m }, называемому искусственным базисом, и имеет неотрицательный столбец свободных членов (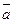 0 ≥ 0). Поэтому ей соответствует исходное опорное решение
0 ≥ 0). Поэтому ей соответствует исходное опорное решение

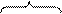 n m
n m
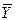 =(0, 0, …, 0, a10 , …, am0 )
=(0, 0, …, 0, a10 , …, am0 )
Рассмотрим любое допустимое решение 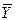 = (а1, а2,..., аn, аn+1, …, аn+m) исходной системы.
= (а1, а2,..., аn, аn+1, …, аn+m) исходной системы.
Если в этом решении все искусственные переменные равны нулю (аn+1= … аn+m=0), то первые n чисел определяют допустимое решение(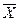 =(а1, а2, …, аn ) системы.
=(а1, а2, …, аn ) системы.
Наоборот, если 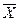 =(а1, а2, …, аn) есть допустимое решение системы, то
=(а1, а2, …, аn) есть допустимое решение системы, то
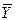 =(а1, а2, …, аn , 0, …, 0)
=(а1, а2, …, аn , 0, …, 0)  есть допустимое решение системы.
есть допустимое решение системы.
По этой причине будем решения 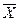 =(а1, а2, …, аn) и
=(а1, а2, …, аn) и 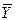 =(а1, а2, …, аn , 0, …, 0) называть соответствующими.
=(а1, а2, …, аn , 0, …, 0) называть соответствующими.
Составим новую целевую функцию:
T=z – M * 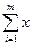 n+i =
n+i = 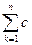 k* xk -M*
k* xk -M* 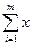 n+i
n+i
где М — произвольно большое число, и будем максимизировать ее в области допустимых решений исходной системы.
Полученными соотношениями определяется новая задача, которую назовем М-задачей.
Эта задача может решаться симплексным методом. При этом на основании вышеизложенного через конечное число итераций либо будет найдено ее оптимальное решение, либо установлено, что функция Т → ∞.
Оказывается, что между оптимальными решениями М-задачи и исходной существует связь, устанавливаемая следующей теоремой.
Теорема 1. Если в оптимальном решении М-задачи 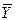 = (b1, b2,..., bn, bn+1, …, bn+m) все искусственные переменные равны нулю (т. е. аn+i = 0 для всех i), то соответствующее решение
= (b1, b2,..., bn, bn+1, …, bn+m) все искусственные переменные равны нулю (т. е. аn+i = 0 для всех i), то соответствующее решение 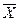 =(b1, b2, …, bn) есть оптимальное решение исходной задачи.
=(b1, b2, …, bn) есть оптимальное решение исходной задачи.
Теорема 2. Если имеется оптимальное решение М-задачи, в котором хоть одна из искусственных переменных отлична от нуля, то система ограничений исходной задачи несовместна в области допустимых решений.
Теорема 3. Если М-задача оказалась неразрешимой (Т → ∞), то исходная задача также неразрешима либо по причин несовместности системы (23) в области допустимых решений, либо по причине неограниченности функции z (zmax → ∞).
Рассмотрим практическое применение метода искусственного базиса.
Дана математическая модель задачи:
F (x) = 5x1 + 6x2 + 7x3 + 4x4 → min
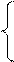 |
x1 + x2 + 4x4 > = 26
2x1 + 3x3 + 5x4 > = 30
x1 + 2x2 + 4x3 + 6x4 > = 24
xj > =0 j = 1÷ 4
Приведем задачу к канонической форме:
F (x) = 5x1 + 6x2 + 7x3 + 4x4 → min
F (x) = -5x1 -6x2 -7x3 - 4x4 → max
Введем балансовые переменные х5, х6, х7
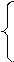 x1 + x2 + 4x4 – x5 = 26
x1 + x2 + 4x4 – x5 = 26
2x1 + 3x3 + 5x4 – x6 = 30
x1 + 2x2 + 4x3 + 6x4 – x7 = 24
Т.к. введенные балансовые переменные имеют знак «-», то принять их за базисные нельзя.Поэтому введем искусственные переменные х8, х9, х10.
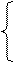 x1 + x2 + 4x4 – x5 + x8 = 26
x1 + x2 + 4x4 – x5 + x8 = 26
2x1 + 3x3 + 5x4 – x6 + x9 = 30
x1 + 2x2 + 4x3 + 6x4 – x7 + x10 = 24
xj > =0 j = 1÷ 10
Заполним симплексную таблицу и используя алгоритм модифицированного симплексного метода найдем оптимальное решение.
Так как среди элементов оценочной строки нет ни одного отрицательного, то решение считается оптимальным.
F (x)min = - F(x)max = - (-26) = 26
x = (0, 0, 0, 13/2, 0, 5/2, 15, 0, 0, 0)
Таблица 4. Симплексная таблица
| Cij | Xi | Bi | -5 | -6 | -7 | -4 | -M | -M | -M | Bi/Aip | |||
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | ||||
| -M | x8 | -1 | 13/2 | ||||||||||
| -M | x9 | -1 | |||||||||||
| -M | x10 | -1 | |||||||||||
| ∑ | -80 | -4 | -3 | -7 | -15 | ||||||||
| -M | x8 | 1/3 | -1/3 | -8/3 | -1 | 2/3 | |||||||
| -M | x9 | 7/6 | -5/3 | -1/3 | -1 | 5/6 | |||||||
| -4 | x4 | 1/6 | 1/3 | 2/3 | -1/6 | - | |||||||
| ∑ | -20 | -3/2 | -3/2 | ||||||||||
| -M | x8 | -3/5 | -12/5 | -1 | 4/5 | ||||||||
| x7 | 7/5 | -2 | -2/5 | -6/5 | - | ||||||||
| -4 | x4 | 2/5 | 3/5 | -1/5 | - | ||||||||
| ∑ | 3/5 | -1 | 12/5 | -4/5 | |||||||||
| -6 | x2 | -3/5 | -12/5 | -1 | 4/5 | 5/2 | |||||||
| x7 | 1/5 | -26/5 | -2 | 2/5 | |||||||||
| -4 | x4 | 2/5 | 3/5 | -1/5 | - | ||||||||
| Z | -4 | ||||||||||||
| x6 | 5/2 | -3/4 | 5/4 | -3 | -5/4 | ||||||||
| x7 | 1/2 | -1/2 | 28/5 | -3/2 | |||||||||
| -4 | x4 | 13/2 | 1/4 | 1/4 | -1/4 | ||||||||
| Z | -26 |
Контрольные вопросы и упражнения
- Какая задача называется М-задачей?
- Что называется оптимальным планом задачи с искусственным базисом?
- Как привести задачу линейного программирования к
- канонической форме, если неравенства системы
- ограничений имеют разнородные знаки?
- Каким образом заполняется симплексная таблица?
- Как вычисляется строка суммы?
- С какой целью вводится строка суммы?
- Каким образом осуществляется переход к следующей итерации?
- Что происходит с искусственной переменной после выхода из базиса?
- Как влияет на ход решения задачи наличие искусственной переменной в оптимальном плане?
- Дайте сравнительную характеристику методов для решения стандартной задачи ЛП и М-задачи.
- Решить симплексным методом следующие М-задачи линейного программирования:
а) F(x)= -7x1+3x2 g max
 2x1+3x2-4 > _ 12
2x1+3x2-4 > _ 12
-x1+x2 < _ 7
-2x1+x2 < _ 10
x1 > _ 0, x2 > _ 0
Ответ: F(x)=21; X=(0, 7, 5, 0, 3, 0)
б) F=x1+x2 g max
 x1+2x2 < _ 10
x1+2x2 < _ 10
x1+2x2 > _ 2
2x1+x2< _ 10
x1 > _ 0, x2 > _ 0
Ответ: F(x)=20/3; X=(10/3; 10/3; 8; 0; 0; 0)
в) F=x1-x2 g max
 -2x1+x2 < _ 2
-2x1+x2 < _ 2
-x1+2x2 > _ 8
x1+x2< _ 5
x1 > _ 0, x2 > _ 0
Ответ: нет решения
г)F=2x1-6x2 g max
 x1+x2 > _ 2
x1+x2 > _ 2
-x1+2x2 < _ 4
x1+2x2< _ 8
x1 > _ 0, x2 > _ 0
Ответ: F(x)=16; X=(8; 0, 6; 12; 0; 0)
|
|