
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Направление математики, изучающее методы решения экстремальных задач, которые характеризуются линейными зависимостями между переменными и линейным критерием, называется
|
|
- линейное программирование;
- моделирование;
- экстремальное программирование.
2. Стандартной задачей линейного программирования называется задача, которая состоит в определении…:
1. минимального значения целевой функции F(x)=C1X1+C2X2+…+CnXn → 1, при выполнении условий (ограничений в виде неравенств и условий неотрицательности);
2. максимального значения целевой функции F(x)=C1X1+C2X2+…+CnXn → MAX(MIN), при выполнении условий (ограничений в виде неравенств и условий неотрицательности);
3. базисного значения целевой функции F(x)=C1X1+C2X2+…+CnXn → MAX, при выполнении условий (ограничений в виде неравенств и условий неотрицательности);
3. Необходимым условием постановки задачи линейного программирования является…:
1. наличие критерия оптимальности и условия сохранения линейности между целевой функции и ограничениями;
2. условие равенства между запасом груза в пунктах отправления и потребностями в грузе в пунктах назначения;
3. наличие критерия оптимальности и ограничений на наличные ресурсы, на величину спроса, на производственную мощность и другое;
4. Критерием оптимальности называется…:
1. показатель, который характеризует моделируемый объект;
2. показатель, по которому оценивается мера эффективности плана, его оптимальность;
3. показатель, который позволяет исследовать изменение экономического процесса;
5. В общем виде целевая функция задачи линейного программирования выглядит следующим образом…:
1.F(x)=C1X1+C2X2+…+CnXn → MAX(MIN);
2.F(d)=dX1+dX2+…+dXn → 1;
3.F(x)=C1X1+C2X2+…+CnXn = 0;
6. Каким ученым был впервые предложен симплексный метод?
1. Данцигом;
2. Вольтером;
3. Никтором.
7. Из какого условия выбирается разрешающая q-я строка?
1. 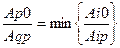 ;
;
2. 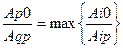 ;
;
3. 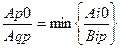 .
.
8. Какую фигуру обозначает термин «симплекс»?
1. простейший треугольник, у которого углы при основании равны;
2. простейший многогранник n – мерного пространства, имеющий n+1 вершин;
3. простейший квадрат.
9. Что не включает в себя алгоритм симплексных преобразований?
1. выбор разрешающего столбца ap из заданных условий;
2. определение количества итераций из заданных условий;
3. выбор разрешающей q – ой строки из заданных условий
10. Что означает наличие в оценочной строке отрицательных элементов?
1. необходимость проведения еще одной итерации;
2. получено решение;
3. решений нет.
11. В каком виде переписывается соответствующая строка (столбец), если в разрешающей строке (столбце) имеется нулевой элемент?
4. с изменением;
5. без изменения;
6. строка не участвует в последующем решении.
12. Для чего в симплексной таблице предназначен последний столбец?
7. для выбора одного разрешающего элемента;
8. для выбора разрешающей строки;
9. для использования его в качестве слагаемого, преобразование которого приведет к нахождению верного решения.
13.Количество базисных переменных должно быть равно количеству ограничений?
1. нет;
2. да;
3. не обязательно.
14. Разрешающий столбец ар выбирается при условии если …
1. оценка а0р< 0 и все элементы аip< 0;
2. оценка а0р> 0 и хотя бы один элемент аip> 0;
3. оценка а0р< 0 и хотя бы один элемент аip> 0.
15.Какими свойствами обладают базисные переменные?
1. они входят с коэффициентом, равным единице только в одно уравнение и с коэффициентом, равным нулю в остальные уравнения системы;
2. они входят с коэффициентом, равным нулю только в одно уравнение и с коэффициентом, равным единице в остальные уравнения системы;
3. они входят с коэффициентом 1 и 0 в любое уравнение системы.
16. Пересчет элементов разрешающей i – й строки производится по формуле …
1. a'ik=. a'ik-aip*aqk;
2. a'qk=aqk/aqp(k=0, 1, …, n).
3. a'qk=aqk/aqp(k< 0);
|
|