
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вторая теорема двойственности
|
|
Пусть взаимно двойственные задачи представлены в симметричной форме
|
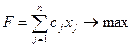
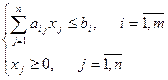
|

Рассматриваемая ниже теорема позволяет утверждать, что на оптимальных решениях прямой и двойственной задач выполняется условие: для каждой пары понятий: (переменная одной задачи – соответствующее ограничение другой) или переменная обращается в ноль, или ограничение выполняется как равенство.
Теорема 2: для того, чтобы допустимое решение прямой задачи 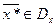 и допустимое решение двойственной задачи
и допустимое решение двойственной задачи 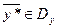 были оптимальными, необходимо и достаточно, чтобы выполнялись условия дополняющей нежесткости:
были оптимальными, необходимо и достаточно, чтобы выполнялись условия дополняющей нежесткости:
|
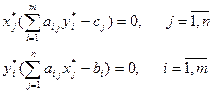
Условия (7)-(8) не означают ничего другого, как только то, что или переменная обращается в ноль, или ограничение выполняется как равенство.
Доказательство:
· Достаточность:
Пусть имеются 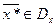 ,
, 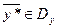 и для них выполняются условия (7)-(8). Покажем, что это оптимальные решения своих задач.
и для них выполняются условия (7)-(8). Покажем, что это оптимальные решения своих задач.
Для этого просуммируем (7) и (8) по j и по i соответственно:
|
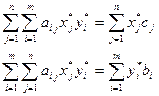
Левые части соотношений (9) и (10) равны, значит, равны и правые, а это критерии целевых функций
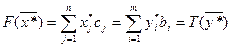
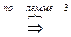
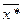 ,
, 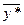 – оптимальные решения.
– оптимальные решения.
· Необходимость:
|
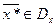 ,
, 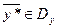 – оптимальные решения. Покажем, что для них выполняются условия (7)-(8). С учетом соотношений (5) и (2) запишем
– оптимальные решения. Покажем, что для них выполняются условия (7)-(8). С учетом соотношений (5) и (2) запишем
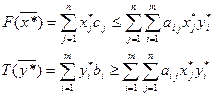
Продолжая неравенство (11) с учетом (12), получим
|
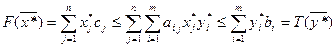
Так как 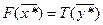 , то каждое неравенство в (13) выполняется как равенство. Рассмотрим первое из них
, то каждое неравенство в (13) выполняется как равенство. Рассмотрим первое из них
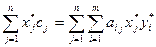
Преобразуем
|
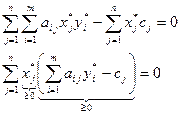
В левой части (14) – сумма неотрицательных слагаемых. Такая сумма равна нулю только тогда, когда каждое слагаемое равно нулю
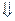
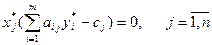
А это и есть соотношения (7).
Аналогично доказываются и соотношения (8).
Теорема доказана.
Экономическая интерпретация второй теоремы двойственности:
1. Если на оптимальном плане продукция производится (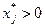 ), то затраты на единицу продукции полностью переходят в доход (
), то затраты на единицу продукции полностью переходят в доход (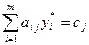 ), то есть технология производства эффективна и потерь нет.
), то есть технология производства эффективна и потерь нет.
2. Если на оптимальном плане затраты на производство единицы продукции превышают доход (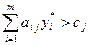 ), то такая продукция не производится (
), то такая продукция не производится (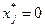 ).
).
3. Если на оптимальном плане оценка ресурса больше ноля (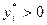 ), то есть, если изменение ресурса увеличивает доход, то ресурс расходуется полностью (
), то есть, если изменение ресурса увеличивает доход, то ресурс расходуется полностью (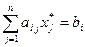 ).
).
4. Если на оптимальном плане ресурс расходуется не полностью (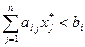 ), то его оценка равна нулю (
), то его оценка равна нулю (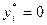 ), то есть изменение этого ресурса (малое) не влияет на критерий.
), то есть изменение этого ресурса (малое) не влияет на критерий.
Соотношения (7) и (8) позволяют по оптимальному решению одной задачи найти оптимальное решение другой.
Вторая теорема двойственности позволяет сформулировать признак оптимальности допустимого решения. Мы уже знаем один признак оптимального решения (теорема 4 главы 3), но он справедлив только для опорного решения (угловой точки области допустимых решений) и фактически требует построения симплекс-таблицы.
Следствие теоремы 2 (двойственный признак оптимальности): для того, чтобы допустимое решение задачи линейного программирования 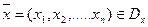 было оптимальным, необходимо и достаточно, чтобы среди решений
было оптимальным, необходимо и достаточно, чтобы среди решений 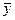 системы уравнений
системы уравнений
|
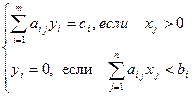
существовало хотя бы одно допустимое решение двойственной задачи
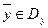 .
.
Решение 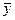 системы уравнений (15) и
системы уравнений (15) и 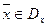 удовлетворяют соотношениям (7) и (8). И если среди решений (15) есть допустимое решение двойственной задачи, то тогда выполняются все условия второй теоремы двойственности и оба эти решения будут оптимальные.
удовлетворяют соотношениям (7) и (8). И если среди решений (15) есть допустимое решение двойственной задачи, то тогда выполняются все условия второй теоремы двойственности и оба эти решения будут оптимальные.
Пример:
Предприятие может работать по двум технологиям. При этом используются два типа ресурсов. Запасы ресурсов составляют 12 тонн и 4 литра соответственно. За 1 час работы по первой технологии расходуется 2 тонны первого ресурса и 1 литр второго, а за 1 час работы по второй технологии – 1 тонна первого ресурса. 1 час работы по первой технологии приносит доход 8 тыс. руб., а по второй – 3 тыс. руб. Суммарное время работы по технологиям должно составлять 6-часовую смену. Определить время работы по каждой технологии так, чтобы суммарный доход был наибольшим.
· Математическая модель
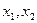 [час] – время работы по каждой технологии
[час] – время работы по каждой технологии
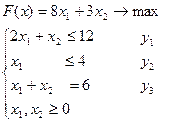
· Построим двойственную задачу.
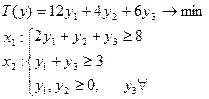
· Проверим, является ли оптимальным решение 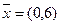 .
.
Для этого запишем соотношения дополняющей нежесткости (7). Подставим в эти соотношения компоненты решения 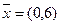
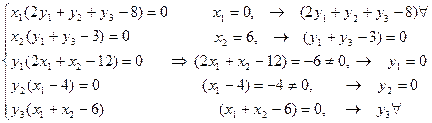
Решая данную систему уравнений, получим 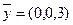 . Подставим
. Подставим 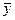 в ограничения двойственной задачи. Первое ограничение не выполняется:
в ограничения двойственной задачи. Первое ограничение не выполняется:
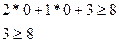
Мы получили, что найденное нами решение 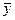 не является допустимым для двойственной задачи. Поэтому можно сделать вывод, что решение
не является допустимым для двойственной задачи. Поэтому можно сделать вывод, что решение 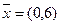 не является оптимальным решением исходной задачи.
не является оптимальным решением исходной задачи.
· Предположим, что нам известно оптимальное решение прямой задачи  , тогда найдем
, тогда найдем 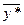 :
:
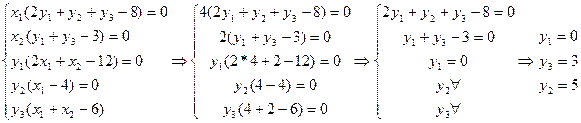
Таким образом, мы получили оптимальное решение двойственной задачи 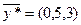 .
.
|
|