Геометрический метод решения задач ЛП.

Решение задачи ЛП геометрически разделяется на этапы:

1. строят прямые, уравнения, которых находят вследствие замены в ограничениях знаков неравенств на знаки равенств;

2. находим полуплоскости, которые определяются из ограничений задачи;

3. определяем многогранник решения;

4. строим вектор ;

5. строим прямую перпендикулярную вектору ;

6. передвигаем прямую из пункта 5 в направлении вектора из пункта 4;

7. определяем координаты крайней точки множества, которой коснется построенная прямая.

8. определяем числовое выражение для целевой функции.

Пример: Р ешим задачу геометрическим методом.

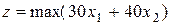
при ограничениях

.

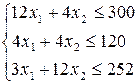
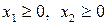Приведем к равенствам систему.

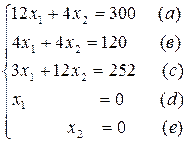
Построим графики прямих, определим область решений задачи.

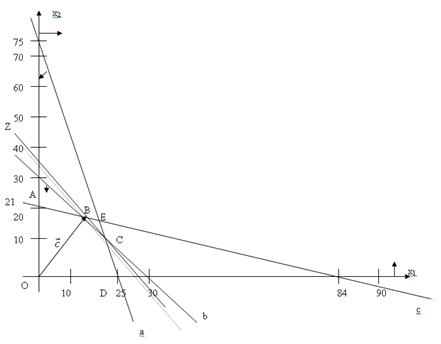
Многогранник решения ОАВСД. Опорные планы – вершины многогранника. Вектор с – отображает направление возрастания значений целевлй функции.Максимальное значение целевой функции достигается в точке В(12, 18) и ее значение вычисляется следующим образом:

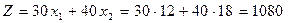
Вопросы для самоподготовки

1. Что называется задачей линейного программирования в канонической форме?

2. Чем определяется область определенности задачи ЛП?

3. Чем определяются опорные планы в графическом методе решения задач ЛП?

4. Какие задачи ЛП можно решать графическим методом?

5. Какие случаи возможные при определении области определенности?

ЛЕКЦИЯ 4.