Задачи математического программирования.

З адача определения оптимальной производственной программы предприятия. Пусть предприятие выпускает 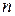найменований изделий (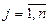). Для их изготовления используется 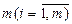найменований ресурсов в количестве 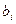каждого. Известна норма расхода 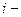го ресурса на единицу 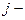го изделия - 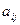. Задана прибыль от продажи единицы 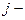го изделия- 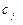. Необходимо составить план производства так, чтобы используя только имеющиеся ресурсы получить максимальную прибыль.

Обозначим через 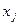- объем выпуска 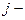го изделия. Тогда математическая модель запишется следующим образом:

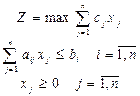
Приведем пример: Изделия N1 и N2 изготовляются на фрезерных станках. Для их изготовления есть 100 кг металла. Затрата металла на изготовление одного изделия N1 составляет 2 кг, а на N2-4кг. Трудоемкость изготовления 100 и 120 станкогодин соответственно для изделий N1 и N2. Мощность фрезерных станков 2000 станкогодин на период, который рассматривается. Составить план производства, которое обеспечивает получение наибольшей выручки от продажи изделий, если отпускная цена одного изделия N1 установлена 3 грн, а изделию N2-2 грн, причем, причем изделий N1 нужно изготовить не больше 40 штук, а изделий N2-не больше 20 штук.

Построим модель данной задачи: Обозначим через х₁- объем выпуска изделия №1, а через х₂ –объем выпуска изделия №2. Тогда модель имеет вид:

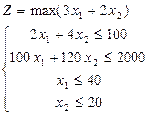
Задача распределения изделий по видам взаимозаменяемого оборудования:

Пусть предприятие выпускает найменований изделий. В объеме (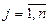) каждого. Для их изготовления используется 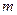видов взаимозаменяемого оборудования. Известен фонд полезного времени для каждого типа оборудования 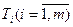. Трудоемкость и себестоимость изготовления изделия зависит от типа оборудования 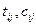. не обходимо выполнить план предприятия с минимальной суммарной себестоимостью.

Обозначим через 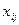- объем выпуска 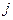-го изделия на 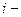ом оборудовании.

Тогда модель задачи имеет вид:

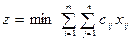
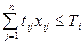
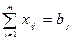
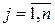
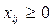
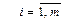
Приведем пример:

	/
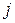
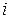
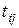
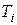
	25/8	12/4	16/5	23/8	14/7	23/8
	15/7	17/6	-	16/6	19/8	17/6
	13/4	14/5	24/8	14/5	-	15/5
	10/3	13/6	12/4	25/8	16/7	10/4
	24/8	12/6	-	19/6	16/8	13/5
bj

Обозначим через 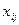- объем выпуска 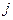-го изделия на -ом типе оборудования. Тогда модель имеет вид:

(; )

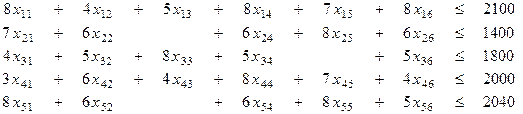
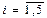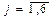Решив эту задачу получим следующее решение.

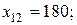
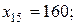
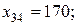
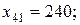
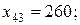
остальные

Проанализируем решение:

1) Распределение изделий по видам оборудования:

На 1-ом типе оборудования изготавливаются изделия 2- го типа в объеме 180 ед и изделия 5 типа в объеме 160 ед.( )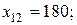

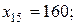На 2 –ом типе оборудования изделия не изготавливаются.

На 3-ем типе оборудования изготавливаются изделия 4- го типа в объеме 170 ед ()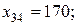

На 4-ом типе оборудования изготавливаются изделия 1- го типа в объеме 240 ед, изделия 3 типа в объеме 260 ед., изделия 6-го типа в объеме 60 ед.( ).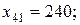

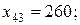
На 5-ом типе оборудования изготавливаются изделия 6- го типа в объеме 140 ед ().

2) Коэффициент загрузки оборудования, вычисляется по формуле:

3) Оптимальный парк оборудования, вычисляется по формуле:

; ; ; ;

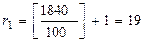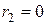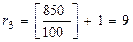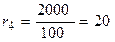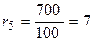
4) Оптимальная себестоимость. Вычисляется как значение целевой функции.

Вопросы для самоподготовки

1. Что определяется в задаче определение оптимальной производственной программы?

2. Что определяет целевая функция в задаче определения оптимальной производственной программы?

3. Что определяет ограничение в задаче определения оптимальной производственной программы?

4. Запишите математическую модель задачи определения оптимальной производственной программы?

5. Что определяется в задаче распределения производственной программы по видам оборудования?

6. Как определить оптимальный парк оборудования для выполнения производственной программы?

7. Запишите математическую модель распределения производственной программы по видам оборудования?

ЛЕКЦИЯ 3.

Линейное программирование.

Формально задача ЛП записывается так:

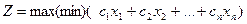(4)

при ограничениях

(5)

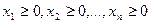(6)

где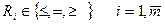

Задача, в которой нужно найти максимум функции (4) при условиях (5), приведенных к равенствам, и условиях (6), называется задачей ЛП в канонической форме.

Канонический вид записи:

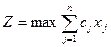(7)

при ограничениях

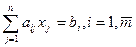(8)

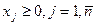(9)

Для задач в канонической форме созданы методы решения. Любая форма записи ЛП задач может быть приведена к каноническому виду путем алгебраических преобразований.

Если целевая функция есть функцией минимизации, то привести ее к виду (7) можно заменой знаков составляющих 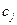. Т.е.

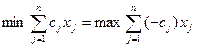
Если ограничения имеют знак 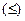, то привести к равенству можно путем введения дополнительных переменных со знаком «+». Т.е.

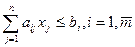
Если ограничения имеют знак , то привести к равенству можно путем введения дополнительных переменных со знаком «-». Т.е.

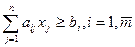
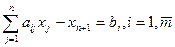
В системе ограничений могут быть неравенства с разными знаками, а так же равенства. Алгебраические преобразования проводят только для неравенств.

Пример:

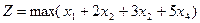
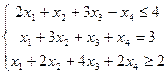
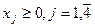
Приведем задачу к каноническому виду:

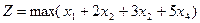
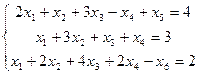
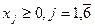
Вектор 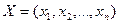, удовлетворяющий ограничениям задачи ЛП (5), называется ее решением либо планом. Если переменные удовлетворяют еще и условиям неотрицательности (6), то Х называется допустимым планом или допустимым решением. Множество R(X) допустимых планов, представляет собой область допустимых решений (ОДР) задачи ЛП, является выпуклым многогранным множеством.

Допустимый план, соответствующий крайней точке множества, является опорным планом или допустимым базисным решением задачи ЛП. Опорный план, обращающий в максимум или минимум целевую функцию, называется оптимальным планом задачи ЛП.