Теоретична частина. Задача 1. Припустимо, що задана вибірка нормальних незалежних вимірювань і їх математичне сподівання й дисперсія дорівнюють і

Задача 1. Припустимо, що задана вибірка нормальних незалежних вимірювань 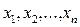і їх математичне сподівання й дисперсія дорівнюють 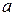і 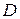. Необхідно перевірити, що математичне сподівання вибіркової дисперсії в дійсності дорівнює .

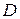Запишемо формулу для обчислення вибіркової дисперсії:

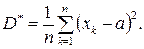
Розділимо цей вираз на 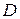й перетворимо до такого вигляду:

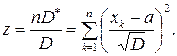
Тут 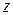– випадкова величина, яка дорівнює сумі нормальних випадкових величин з нульовим математичним сподіванням і одиничною дисперсією. Її закон розподілу ймовірностей відомий: розподіл хі-квадрата з 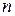степенями вільності:

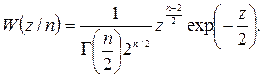
Випадкові величини, що мають закон розподілу хі-квадрат, характеризуються такою властивістю: з імовірністю 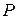має місце нерівність 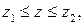де граничні значення 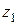й 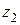дорівнюють

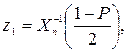
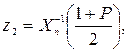
де 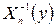– функція, обернена до інтеграла ймовірності хі-квадрата:

.

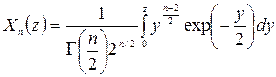Таким чином, вирішальне правило перевірки гіпотези про рівність 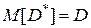формулюється в такий спосіб: якщо обчислене значення вибіркової дисперсії задовольняє нерівність:

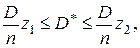(20)

то з імовірністю 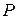можна вважати, що .

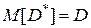Задача 2. Задані дві вибірки нормальних незалежних вимірювань 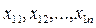та 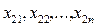з математичними сподіваннями 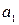і 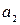й дисперсіями 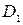і 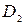відповідно. Необхідно перевірити, що математичне сподівання вибіркової дисперсії 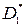дорівнює математичному сподіванню вибіркової дисперсії .

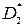Порівняємо дві вибіркові дисперсії

,

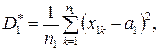
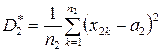для чого розглянемо їх відношення

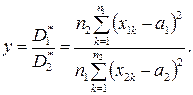
Якщо 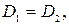то випадкова величина 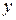підпорядковується закону розподілу Снедекора (закону відношення вибіркових дисперсій)

.

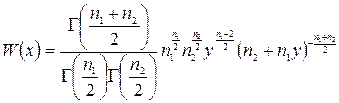У цьому випадку (тобто якщо 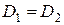) з імовірністю 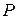випадкова величина 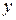задовольняє нерівність 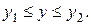Граничні значення 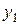й 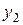обчислюються за формулами, які мають вигляд

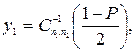
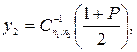(21)

де – функція, обернена до інтеграла ймовірності Снедекора:

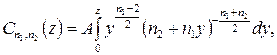
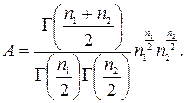
Таким чином, якщо виконується нерівність

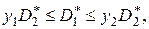(22)

то з імовірністю 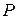можна стверджувати, що дві порівнювані вибірки мають однакові дисперсії ().

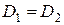Якщо математичні сподівання невідомі, то вибіркові дисперсії оцінюються за формулами

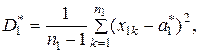
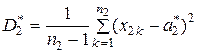
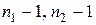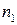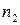і їх відношення має розподіл Снедекора з степенями вільності. Задача порівняння розв’язується так, як було розглянуто вище, а пороги обчислюються за формулами (21), де і необхідно замінити н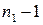а та .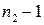

Математичне сподівання й дисперсія розподілу Снедекора дорівнюють

.

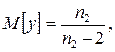
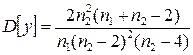Для визначення порогів 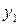та 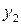варто користуватися таблицями математичної статистики.