
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Арифметические операции с двоичными числами
|
|
При арифметических операциях используются таблицы сложения и умножения и вычитания в двоичной системе
| + | * | - | ||||||||
| 0 (10) | ||||||||||
При двоичном сложении 1 + 1 возникает перенос 1 в старший разряд, как и в десятичной арифметике. Например,
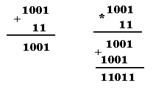
При двоичном вычитании необходимо помнить, что занятая в ближайшем разряде 1, дает две единицы младшего разряда. Если в соседних старших разрядах стоят нули, то 1 занимается через несколько разрядов. При этом единица, занятая в ближайшем значащем старшем разряде, дает две единицы младшего разряда и единицы во всех нулевых разрядах, стоящих между младшим и тем старшим разрядом, у которого бралась единица.
Вычтем 174 из 197

Деление двоичных чисел происходит с использованием двоичных таблиц умножения и вычитания. Разделим 430 на 10

Задания:
Задание 1.. Перевести в двоичную, восьмеричную, семеричную, шестнадцатеричную в системы счисления следующие числа:
1) 123(10); 0, 3(10);
2) 147(10); 0, 47(10).
3) 245(10); 1, 3(10);
4) 432(10) ; 4, 1(10);
5) 312(10); 3, 2(10) ;
6) 81(10). 1, 12(10);
7) 65(10) 0, 1234(10).
8) 37(10) 3.85(10)
9) 111(10) 2.343(10)
10) 98(10) 9.775(10)
11) 137(10) 32.115(10)
12) 55(10) 13.22(10)
13) 42 (10) 3.27(10)
14) 198(10) 2.25(10)
Задание 2. Перевести числа в десятичную систему счисления следующие числа:
1) а) 110011012 = X10; б) FA216 = X10; в) 618 = X10
2) а) 110011002 = X10; б) 3BC16 = X2; в) 578 = X10
3) а) 1012 = X10; б) 34F16 = X2; в) 2388 = X10
4) а) 1001102 = X10; б) AC16 = X2; в) 728 = X10
5) а) 111111002 = X10; б) 52C16 = X2; в) 148 = X10
6) а) 111111112 = X10; б) 3BF16 = X2; в) 518 = X10
7) а) 1111012 = X10; б) 3616 = X2; в) 678 = X10
8) а) 1102 = X10; б) 9216 = X2; в) 228 = X10
9) а) 110111012 = X10; б) 3A16 = X2; в) 1238 = X10
10) а) 11112 = X10; б) A1F16 = X2; в) 158 = X10
11) а) 1110102 = X10; б) D2316 = X2; в) 3848 = X10
12) а) 100011112 = X10; б) 3716 = X2; в) 268 = X10
13) а) 110011002 = X10; б) CF16 = X2; в) 788 = X10
14) а) 110011002 = X10; б) 33C16 = X2; в) 5728 = X10
Задание 3. Перевести следующие числа из двоичной системы счисления в восьмеричную и шестнадцатеричную (минуя десятичную):
1)1110.01(2);
2) 1001.01(2);
3) 100001.110(2);
4)100011.01(2) ;
5)11.11001(2);
6)10000.00001(2).
7) 100111(2);
8) 11111111(2);
9) 1011.01(2);
10) 1001.01(2);
11) 10000101.001(2);
12) 100100.01(2);
13) 11.01(2);
14) 100001.01(2);
Задание 4.Перевести следующие числа в двоичную системы счисления (минуя десятичную):
1) 34(8)
2) A71(16)
3) 614(8)
4) 712(16)
5) 3D1(16)
6) 541(8)
7) 21(8)
8) 741(16)
9) 111(8).
10) 1АF(16).
11) 232(8).
12) 51(16).
13) 138(8).
14) 110(16).
Задание 5. Вычислить:
1 вариант. Перевести числа в двоичную систему и вычислить значения выражений
1) 42-33; б) 153+123; в) 245/8; г) 51*23;
2 вариант. Выполните действия в двоичной системе счисления, ответ дать в десятичной системе:
а) 11001101011 + 1110000101; б) 101011 – 10011; в) 1011 · 101.
3 вариант. Выполните действия в двоичной системе счисления, ответ дать в восьмеричной системе:
а)1110101011 + 1110110101; б) 1100011 - 1011; в) 10101 · 111.
4 вариант. Вычислите значение выражение (А + В) · С, если А = 10112, В = С316, С = 310.
5 вариант. Вычислите сумму чисел X и Y, если X=1100112 Y=1358. Результат представьте в двоичном виде.
6 вариант. Вычислите значение выражение (А + В) · С, если А = 10012, В = A216, С = 710.
7 вариант. Вычислите сумму чисел X и Y, если X=1101112 Y=1578. Результат представьте в двоичном виде.
8 вариант. Вычислите (100012 * 9F16) – 3310. Ответ дайте в виде Х10.
9. вариант. Перевести числа в двоичную систему и вычислить значения выражений
а) 428-338; б) 15316+12310;
10. вариант. Перевести числа в двоичную систему и вычислить значения выражений
а) 2458/810; б) 3110-1310;
11. вариант. Выполните действия в двоичной системе счисления, ответ дать в восьмеричной системе:
а)11111 + 11101101; б) (1100011 – 1011)* 101;
12. вариант. Выполните действия в двоичной системе счисления, ответ дать в восьмеричной системе:
а)(111 * 1101)/10001; б) 11011 +11011;
13. вариант. Вычислите сумму чисел X и Y, если X=11010112 Y=758. Результат представьте в двоичном виде.
14. вариант. Вычислите а) 5610+3D16 = X2 б) (167+ 213)/348=Х2
Задание 6. Записать год рождения, месяц рождения1111, число, (-1)*номер варианта в прямом, обратном, дополнительном коде.
|
|