
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Краткое описание метода касательных при решении нелинейных уравнений
|
|
Министерство образования и науки Российской Федерации
федеральное государственное автономное образовательное учреждение
высшего образования
НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Институт ЭНИН
Специальность Теплоэнергетика и теплотехника
Кафедра АТЭС
ЛАБОРАТОРНАЯ РАБОТА №1
| Тема работы |
| Решение нелинейных уравнений методом касательных. |
Студент
| Группа | ФИО | Подпись | Дата |
| 5Б43 | Карипанов Константин Вячеславович | 05.03.2015 |
Руководитель
| Должность | ФИО | Подпись | Дата |
| Ассистент кафедры АТЭС | Янковский Станислав Александрович |
Томск – 2015 г.
Содержание
Введение……………………………………………………………..3
Краткое описание метода решения нелинейных уравнений..….4-5
Текст программы……………………………………………………6
Результаты вычислений, выводы по работе ………………..…….7
Введение:
Тема: Решение нелинейных уравнений.
Цель: Изучение численных методов решения нелинейных уравнений.
Задачи: Освоить метод половинного деления, метод касательных и модифицированный метод Ньютона для решения нелинейного уравнения, научиться численно определить действенный корень нелинейного уравнения, составить алгоритм и соответствующую программу, развить практические навыки решения задач на ЭВМ.
Условие задачи: Определить с точностью ε температуру поверхности Т твердоготела при радиационно-конвективном теплообмене, если известно экспериментально измеренное значение температуры Тэ в точке, расположенной на расстоянии h от поверхности. Для расчета использовать уравнение
q= α (Tc – T) + ε nσ 0(Тс – Т 4 ), или
λ (Т – Тэ)/h = α (T – T) + ε п σ 0(Тс – Т),
где λ – коэффициент теплопроводности материала тела, Вт/м·К; h – глубина закладки датчика (термопары), м; Тс – температура греющей среды, К; α – коэффициент конвективного теплообмена, Вт/м2·К; ε n – приведенная степень черноты; σ 0 = 5.67⋅ 10-3 Вт/м2К4 – постоянная Стефана-Больцмана.
Исходные данные: λ = 8.5; h = 8⋅ 10-3; Tэ = 953.5; Tс = 1273; α = 25; ε n = 0.3; ε = 0.1.
Краткое описание метода касательных при решении нелинейных уравнений
Метод половинного деления основан на поиске отрезка, содержащего корень и последующим уменьшением его размеров до достижения заданной точности вычислений. Уменьшение размеров отрезка осуществляется циклическим делением его пополам и отбрасыванием половинки, не содержащий корня.
Пусть дано уравнение ƒ (x) = 0, где ƒ (x) – непрерывная функция, корень Р отделен на отрезке [ a, b ], т. е. ƒ (a) ⋅ ƒ (b) > 0, причем | b – a | < E. Требуется найти значение корня Р с точностью до Е (см. рис. 1).
Если корень Р не отделен на заданном отрезке, т. е. ƒ (a) и ƒ (b) одного знака и, следовательно, ƒ (a) ⋅ ƒ (b) > 0, то вычисляются значения функции в точках, расположенных через равные интервалы на оси Х. Когда ƒ (an) и ƒ (bn) имеют противоположные знаки, то значения a = an и b=bn принимаются в качестве начальных и находят середину отрезка [ a, b ], т. е. с= (a+b)/2. Тогда отрезок [ a, b ] точкой с разделится на два равных отрезка [ a, c ] и [ c, b ], длина которых равна (b – a)/2. Из двух этих образовавшихся отрезков выбирается тот, на концах которого функция ƒ (x) принимает значения противоположных знаков; обозначим его [ a 1, b 1]. Затем отрезок [ a 1, b 1] делим пополам и проводим те же действия. Получим отрезок [ a 2, b 2], длина которого равна (b – a)/22. Процесс деления отрезка пополам производится до тех пор, когда на каком-то k -м этапе будет получен отрезок [ ak, bk ], такой, что
bk – ak = (b – a) / 2 k ≤ E и ak ≤ P ≤ bk,
где число k указывает на количество проведенных делений. Числа ak и bk – корни уравнения ƒ (x) = 0 с точностью до E. За приближенное значение кор-ня следует взять Р= (ak+bk) / 2, причем погрешность не превысит (b – a)/2 k+ 1.
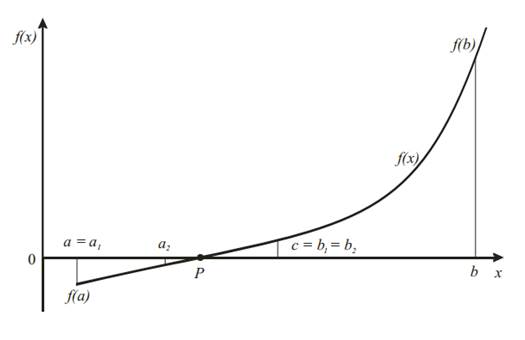
Рисунок 1 Графическая интерпретация метода половинного деления
Отметим, что в качестве условия прекращения счета более целесообразно пользоваться условием E ≥ ⎜ bk – ak⎢.
Рассмотренный метод имеет относительно малую скорость сходимости, но отличается от других методов простотой реализации алгоритма, не требующего вычисления производных заданной функции.
Текст программы:
Program laba1;
uses crt;
Function f(m: real): real;
Begin
f: =m-sin(m)/cos(m);
end;
var a, b, c, k, e, m: real;
begin
write('b='); read(b);
write('k='); read(k);
write('e='); read(e);
a: =b;
b: =a+k;
If f(a)*f(b)< 0 then
c: =(a+b)/2
else begin
a: =b;
b: =a+k;
c: =(a+b)/2;
end;
Repeat
If f(a)*f(c)< 0 then
b: =c
else
a: =c;
c: =(a+b)/2;
until
abs(b-a)< =e;
writeln('x=', (a+b)/2-3.14);
end.
Результат:
При решении задачи методом половинного деления в программе Pascal были получены следующие значения, представленные на рисунках 2, 3:
 При π < μ 2 < 2π
При π < μ 2 < 2π
Рисунок 2 Результаты вычислений
 При 2π < μ 3 < 3π
При 2π < μ 3 < 3π
Рисунок 2 Результаты вычислений
Вывод:
В ходе данной работы был изучен метод половинного деления для нелинейных уравнений, написана программа для данной задачи. Приблизительные значения корней данного уравнения соответствуют действительности.
|
|