
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Реализация в МКЭ. Для численного интегрирования выражения (4.10) используется обратная схема Эйлера, которая гарантирует
|
|
Для численного интегрирования выражения (4.10) используется обратная схема Эйлера, которая гарантирует, что полученные напряжения, деформации и внутренние параметры соответствуют поверхности текучести. Алгоритм включает в себя следующие шаги:
1. Определяется значение параметра σ y для материала для настоящего шага по времени (например, предел текучести при текущей температуре).
2. Вычисление напряжений основывается на пробных деформациях { ε tr }, получаемых как разность полных деформаций и пластических деформаций на предыдущем шаге:
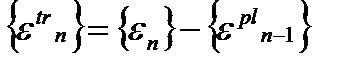 , (4.14)
, (4.14)
где n – индекс номера шага интегрирования.
Соответственно пробные напряжения равны:
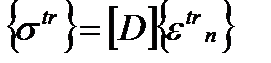 . (4.15)
. (4.15)
3. Определяем эквивалентные напряжения σ e в соответствии с условием (4.4). Если σ e меньше, чем σ y, то материал остается упругим и пластические деформации не рассчитываются.
4. Если же эквивалентные напряжения превышают предел текучести, то для шага интегрирования рассчитывается пластический коэффициент λ по формуле (4.13).
5. Определяем приращение пластических деформаций {Δ ε pl } с помощью формулы (4.6).
6. Текущие пластические деформации получаем как:
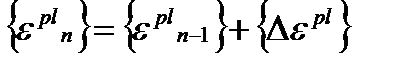 , (4.16)
, (4.16)
а текущие упругие деформации получаем как:
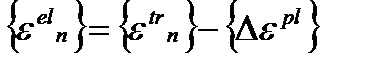 , (4.17)
, (4.17)
откуда можем получить вектор текущих напряжений:
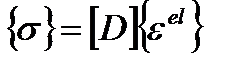 . (4.18)
. (4.18)
7. Приращение пластической работы Δ κ и перемещение поверхности текучести { α } рассчитывается по формулам (4.8) и (4.9), а текущие значения определяются как:
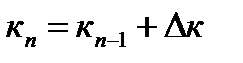 , (4.19)
, (4.19)
и
 . (4.20)
. (4.20)
8. Также вычисляются такие параметры как эквивалентные пластические деформации 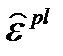 , приращение эквивалентных пластических деформаций
, приращение эквивалентных пластических деформаций 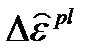 , эквивалентные пластические напряжения
, эквивалентные пластические напряжения 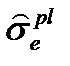 и коэффициент напряжений N.
и коэффициент напряжений N.
Коэффициент напряжений получается как отношение:
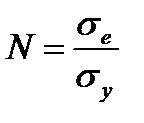 , (4.21)
, (4.21)
где σ e – эквивалентные напряжения, полученные на шаге 3 из вектора пробных напряжений.
Приращение эквивалентных пластических деформаций определяется как:
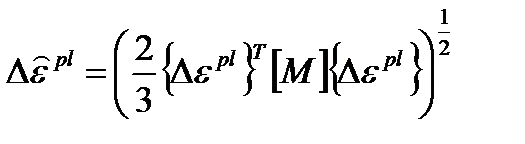 , (4.16)
, (4.16)
а сама величина эквивалентных пластических деформаций:
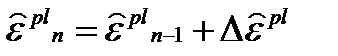 . (4.17)
. (4.17)
|
|